
Journal of 生物数学学报2002,17(3)363-368 Biomathematics 利用P1、F1、P2、F2和F23家系 五世代联合分离分析的拓展 章元明盖钧镒 (南京农业大学大豆研究所,国家大豆改良中心,江苏南京210095) 摘要:在王建康等的基础上拓展了利用P1、F1、P2、F2和F23家系5群体的2 对主基因(B)和2对主基因+多基因(E)2类模型为使拓展模型成为可能并提高分布参数估 计值的精度,用IECM算法估计样本似然函数分布参数.通过重新分析3个大豆杂交组合抗豆 秆黑潜蝇主茎虫量遗传资料证实了通过孟德尔氏遗传分析法所获得的结果,并得到存在多基因的 统计学依据 关键词:主基因+多基因混合遗传;IEC'M算法;数量性状;大豆,豆秆黑潜蝇 中图分类号:Q348 MR.分类号:62J10:921)10 文献标识码:A 文章编号:10019626(2002)03-036306 0引言 在混合遗传分析中,利用多个分离世代联合检测植物数量性状QTL体系的精度比利用个 别世代的高对于杂交困难的作物,可利用P1、F1、P2、F2和F23家系5群体进行 联合分离分析,王建康和盖钧镒提出了利用这5世代的联合分离分析方法,其基本原理和 过程是:(1)假定每一分离世代为多个围绕主基因型由多基因和环境修饰而成的正态分布的混 合分布;(2)在各种假定下建立遗传模型,并得到相应的样本似然函数,采用EM算法获 得样本的极大似然函数值及其极大值点;(3)通过AIC准则选择一个或几个较优模型,并通过 适合性检验确定最优遗传模型;(4)估计相应遗传参数;(5)对分离群体的个体或家系的主基 因型进行Bayes归类.然而,文献[3]只涉及1对主基因(A)、多基因(C)和1对主基因+多 基因(D)3类模型,这时最多只能鉴定出效应最大的主基因,不管次大效应的主基因效应多大 都归入多基因综合考虑.因此很有必要拓展模型类型,扩大该方法的适应范围,本文在王建康 等基础上拓展2对主基因(B)和2对主基因+多基因(E)2类模型.为使模型拓展成为可 能并提高混合分布参数估计值的精度,采用IE(M算法以获得样本似然函数分布参数的极大 似然估计值 收稿日期:20000410 基金项目:江苏省自然科学基金项目、国家973项目和重庆市科委应用基础研究项目 作者简介:章元明(1965),男,重庆永川人,南京农业大学教授,博士 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http:/www.cnki.net
生 物 数 学 学 报 , · 〔 工 。 利用 、 , 、 、 和 家系 五世代联合分离分析的拓展 章元 明 盖钧槛 南京农业大学 大豆研究所 , 国家大豆改 良中心 , 江苏 南京 。。 句 在王 建康等 的基础上 拓展 了利 用 、 , 、 、 和 家系 污 群体 的 对主 基 因 勺 和 对 主 基 因 多基 因 类模 型 为使 拓展模型成为可 能 并提 高分 布参数 怡 计值 的猜度 , 用 算法估计 样本似 然 函 数 分布 参数 通过 重 新分 析 个大 豆 杂交组 合杭 豆 秆 黑 潜绳主 茎 虫量遗传 资料证 实 了通 过 孟德 尔 氏遗 传分析 法所 获得的结果 , 并得到 存在 多基因 的 统计 学依据 关键词 主 基 因 十 多基 因混 合遗传 以 ’ 葬法 数 量性 状 大 豆 , 豆 杆 嗽 潜蝇 中图分类号 分类号 论 , 文献标识码 文章编号 一 一 引 言 在混合遗传分析中 , 利用多个分离世代联合检测植物数量性状 体系的精度 比利用个 别世代的高 一 】对于杂交困难的作物 , 可利用 、 、 、 和 家 系 群体进行 联合分离分析 王建康和 盖钧谧 提 出了利用这 世代的联合分离分析方法 其基本原理和 过程是 假定每一分离世代为多个围绕主基因型 由多基因和环境修饰而成 的正态分布的混 合分布 在各种假定下建立遗传模型 , 并得 到相应的样本似然函数 , 采用 算法 获 得样本的极大似然函数值及其极大值点 通过 准则选择一个或几个较优模型 , 并通过 适合性检验确定最优遗传模型 估计相应遗传参数 对分离群体的个体或家系的主基 因型进行 归类 然而 , 文献 只涉及 对主基 因 、 多基因 和 对主基 因 多 基因 , 类模型 , 这时最多只能鉴定出效应最大的主基 因 , 不管次大效应 的主基 因效应多大 都归入多基 因综合考虑 因此很有必要拓展模型类型 , 扩大该方法的适应范 围 本文在王建康 等 基础上拓展 对主基 因 和 对主基 因 十 多基因 类模型 为使模型拓展成为可 能并提高混合分布参数估计值的精度 , 采用 以 ‘ 算法 以获得样本似然函数分布参数的极大 似然估计值 收稿日期 荃金项 目 作者简介 江苏省 自然科学基金项 目 、 国家 项 目和重庆市科委应用基础研究项 目 章元明 , 男 , 重庆永川人 , 南京农业大学教授 , 博士

4 牛物数学学报 第17卷 1理论推演 1.1基本假定与遗传模型 对亲本,和P,及其杂交、同交世代的遗传体系所作的基本假定与文就B引相同,有关各 aaBB,aaBh和a阳bM,及其相应的主基因型家系按孟德尔分离比例的混合,即分别为9个正态 分布U和)按孟德尔分离比例的混合.亲本和同质群体均表现为单一正 态分布,其分布通式为 1g上~1/16.(1,+1/8.N42.+1/小613:a+1/8.141.i+ 1/4.V(46)+1/8.N(.)+/I6N(.)+1/8.v(s.)+1/16N(.) 123a~1/16.N(61,i)+1/8Y(5go)+1/16.V(U6a,)+1/8.(54,o3+ 1/4.Y(Ur55,)+1/8.Yu65:)+1/16.(u,3z}+1/N(5s.a)+1/16.(u.a5) 由此,可构造样本似然函数 ()=Πen4,)Ⅱf,?2)Ⅱf3a.)Π∑fr4:ha,) 其中,八x:4,σ)是正态分布(μ,a)的密度函数,和妇分别是F2和F2群体的成分 分布数.在各遗传模型下,成分分布数、独立分布参数数、一阶分布参数间约束条件数以及一 阶遗传参数等总结于表【 1.2样本似然函数中成分分布参数极大似然估计的IECM算法 采用BC算法获得样本似然函数中分布参数的极大似然估计值.它包括E步骤和迭代 ('1步骤.E步骤的完全数据对数似然函数的期望函数为 b-()= kg4:mo+ uir logf八rt..o) i1~rk,为样本各观测值的Bs后验概率.迭代('1步骤是分步骤 地计算,)0的条件极大值和极大值点.选代(:步:在固定多基因方差组分a=4.司 和误差方差条件下求分布平均数的条件极大似然估计值;迭代('2步:在固定迭代(', 步中获得的分布平均数和”条件下求多基因方差组分U=4.)的条件极大似然估计值 迭代(,步:在固定选代(3,和选代(,步骤得到的分布平均数和多基因方差组分下求 C 1994-2009 China Academic Joural Electronic Publishing House.All rights reserved.http://www.enki.net
州 牛 物 数 学 学 报 第 卷 理论推演 基本假定与遗传模型 对亲本 和 及其杂交 、 回交世代的遗传体系所作的基本假定 与文献 一 司相同 , 有关各 世代的符号和参数 与文献【 相同 当 亲本有 对主基因差异且主基 因表现为加性 一 显性 上 位性时 , 群体及其 家系群体分别为 种主基因型 八八 刀刀 , 八刀 , 儿飞 几。 刀刀 八。 劲 。 。品 。 。 召 , 。 。 娜 和 。 。品 , 及其相应的主基 因型家系按孟德尔分离 比例的混合 , 即分别为 个正 态 分布 丫 , 。, 和 ’ 你 峭 了 按孟德尔分离比例的混合 · 亲本和 , 同质群体均表现 为单一正 态分布 , 其分布通式为 尸, , 一 州刀 护 几 二 一 八 尸 尸 几 勿 、 一 、 一 尸 , 尸 , 。 , 一 一 , 。、 , 二牙十 、 ‘ 一 , , 二育 一 入 , , , 二才 、 , 。 二戈 ’ 内 端 州尸魂 , 端 ’刀 , 叮 ‘ 州 , 心 、’ 。 , 心 了 一 州 , , 嵘 州户 《 一 、 一 俩 嵘 , 、 一 。。 , 嵘 、 州尸 , 式 。 十 州 。, 心 十 〔 ‘ ’尸 , 嵘 ’ , 心 ’。。,。 叮 。 由此 , 可构造样本似然函数 月 , 为 厂 二 , , , 二 ’, , , , 二 , , , , 二 艺 二 。艺 魂 , 、 二才 了 艺 了之 介 艺 二 · , ‘ ‘ 汀舅 。 公 其中 , 芍 尸 , 尹 是正 态分布 万 尸 , 尹 的密度 函数 , 和 分别是 和 , 群体的成分 分布数 在各遗传模型下 , 成分分布数 、 独立分布参数数 、 一阶分布参数间约束条件数以及一 阶遗 传参数等总结于表 样本似然函数 中成分分布参数极大似然估计的 算法 采用 算法获得样本似然 函数 中分布参数的极大似然估计值 它包括 步骤和迭代 ’ 步骤 步骤的完全数据对数似然函数的期望 函数为 冷 了飞 “州 州“卜 艺 二 , 。 · 二 卜 艺 人 , · , , , 二 艺 , · , , , , , 二 八 几 介 艺艺 , , , ‘ , 二 , 、弓, 二才 艺艺 二 , , 〕 、 厂 二 , 了 , 二舅 , 了 其中 , ‘, 一 断 , 、 二 。, 一 二 、 为样本各观测值的 山 ” 后验概率 迭代 步骤是分步骤 地计算 人、 ’山 的条件极大值和极大值点 · 迭代 ’ 步 在 固定多基 因方差组分 叮 。 二 习 和误差方差 二 条件下求分布平均数的条件极大似然估计值 迭代 ’ 步 在 固定迭代 步 中获得 的分布平均数和 二 条件下求多基 因方差组分 叮 。 、 二 “ 、 的条件极大似然估计值 、 迭代 竹 步 在 固定迭代 〔 ’ 和迭代 步骤得到的分布平均数和多基 因方差组分下求 二
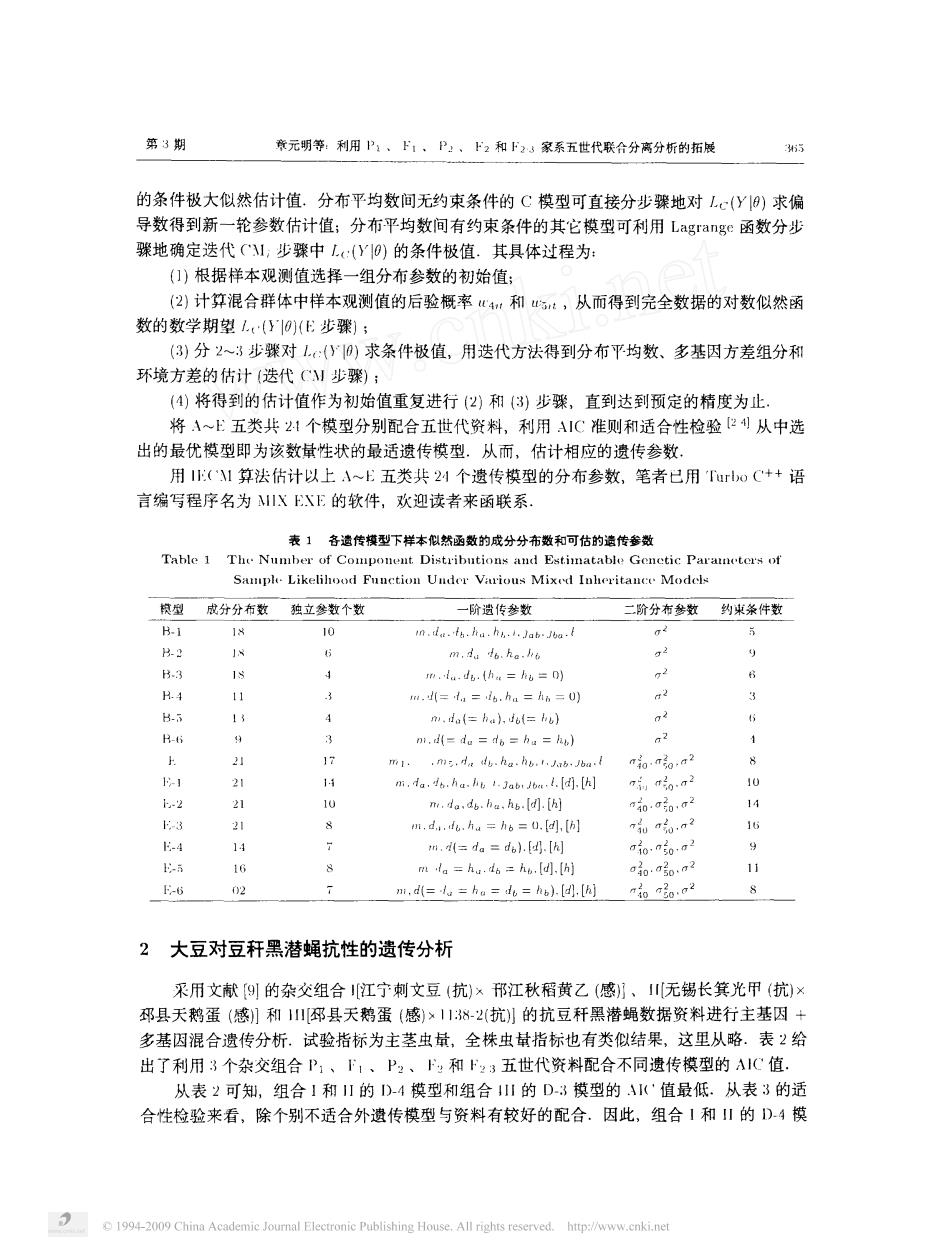
第3期 素元明等:利用P、1,P、下2和F3家系五世代联合分离分析的拓候 355 的条件极大似然估计值.分布平均数间无约束条件的C模型可直接分步骤地对L(Y9)求偏 导数得到新一轮参数估计值:分布平均数间有约束条件的其它模型可利用Lagrange函数分步 骤地确定选代C1,步骤中L:(Y0)的条件极值.其具体过程为: )根据样本观测值选择一组分布参数的初始值: (2)计算混合群体中样本观测值的后验概率心4和,从而得到完全数据的对数似然深 数的数学期望()(E步骤); (3)分2~3步骤对1:()求条件极值,用选代方法得到分布平均数、多基因方差组分和 环境方差的估计(迭代C步骤): (4)将得到的估计值作为初始值重复进行(2)和(3)步骤,直到达到预定的精度为止 将A~E五类共2个模型分别配合五世代资料,利用IC准则和适合性检验2刂从中选 出的最优模型即为该数量性状的最适遗传模型。从而,估计相应的遗传参数 用:(C1算法估计以上A~E五类共24个遗传模型的分布参数,笔者已用Ta心C+语 言编写程序名为MIX EXE的软件,欢迎读者来函联系. 表1各造传模型下样本似然函数的成分分布数和可估的遠传参数 Table 1 The Nu 筑型皮分分布数独立参数个数 一阶遗仿杂数 二阶分布参数约求条作数 H 21 =0) 2 H.3 mi. 2241; 22 14 0 2 10”50 40 02 2大豆对豆秆黑潜蝇抗性的遗传分析 采用文献9的杂交组合江宁刺文豆(抗)x邗江秋稻黄乙(感}、川无锡长箕光甲(抗× 邳县天鹅蛋(感1和1川邳县天鹅蛋(感)、11382抗的抗豆秆黑潜蝇数据资料进行主基因+ 多基因混合遗传分析。试验指标为主茎虫量,全株虫指标也有类似结果,这里从略。表2给 出了利用3个杂交组合P,、1、P:、和下:3五世代资料配合不同遗传模型的AC值. 从表2可知,组合1和I的D-4模型和组合1的D3模型的4('值最低.从表3的适 合性检验来看,除个别不适合外遗传模型与资料有较好的配合。因此,组合1和山的D4模 19-009 Chna Academie Electronic Publishing House.All rights://www
第 期 章元 明等 利用 、 、 尸 、 和 家系五世代联合分离分析的拓展 的条件极大似然估计值 分布平均数间无约束条件的 模型可直接分步骤地对 大 求偏 导数得到新一轮参数估计值 分布平均数间有约束条件的其它模型可利用 即 函数分步 骤地 确定迭代 ” 步骤 中 〔 丫 内 的条件极值 其具体过程为 根据样本观测值选择一组分布参数的初始值 幻 计算混合群体中样本观测值的后验概率 ,翔 , , 和 二 , , 从而得到完全数据的对数似然 函 数的数学期望 儿〔 , 们 步骤 分 一 步骤对 。 , 求条件极值 , 用迭代方法得到分布平均数 、 多基 因方差组分和 环境方差 的估计 迭代 步骤 将得到的估计值作为初始值重复进行 和 步骤 , 直到达 到预 定的精度为止 将 一 五类共 个模型分别配合五世代资料 , 利用 准则 和适合性检验 , “ 从 中选 出的最优模型 即为该数量性状 的最适遗传模型 从而 , 估计相应的遗传参数 用 比 ‘ 算法估计 以上 入一 五类共 别 个遗传模型 的分布参数 , 笔者 已用 ‘ · 〔 ’ 语 言编写程序名为 川 的软件 , 欢迎读者来函联 系 表 各遗传模型下样本似然函数的成分分布数和可估的遗传参数 、 川 〕 川 川 · 川 , ‘ · 写 一 、 〔川 一 工 〕 、 、 〔 、 一 义 · 模型 成分分布数 独立参数个数 一 一 阶遗传参数 二阶分布参数 约束条件数 丁 之 今 叮 ‘八注 ‘ 一︸﹄ 一 日 一 亏 今 一 〔 心 人。 肠 ‘ 子 ‘ 。 乙 了乙。 一 敌 尽 九 人。 人 了。 九 人 、 人。 。 汀 洲二 定 , 理。 人 人, 二 。 、 。 人。 , 九 协 , , 。 理、 , 。 。 二 厅 乃 超 之 占 人。 人产 , 少。 占 , 。 拭。 了、 。 。 , 。 。, 、。, 【己〕 , 【 〕 。认 。 , 以。 。 , 。 【 」人 、 己 。 , 。 、。 。 【己 , 【入 二 以二 。 。 刃 创 二 厅。 二 人 崖。 二 ‘ , 司 , 【叼 了 , 创 、。 二 人 , 己。 人。 【司 , 【司 厅 厅 厅 嘴 。 峭 。 二 汀 万 叮 三。 , 口 戈 。 · 。 圣 。 , 二 二 军 。 二 才 。 , 。 心 。 。 若 。 。 矛 。 二 呈 。 , 二 二 才 。 二 呈 。 , 。 魂 弓 一 大豆对豆秆黑潜蝇抗性的遗传分析 采用文献 回 的杂交组合 江宁刺文豆 抗 邢江秋稻黄乙 感 〕 、 川无锡长箕光 甲 抗 沐 邱县天鹅蛋 感 和 川 邢县天鹅 蛋 感 招 一 抗 的抗豆秆黑潜蝇数据资料进行主基 因 多基 因混 合遗传分析 试验指标为主茎虫量 , 全株虫量指标也有类似结果 , 这里从略 表 给 出了利用 个杂交组合 、 、 、 户 和 , 五世代资料配合不 同遗传模型的 川 值 从表 可知 , 组合 和 的 一 模型和组 合 川 的 一 模型的 值最低 从表 的适 合性检验来看 , 除个别不适合外遗传模型 与资料有较好的配合 因此 , 组合 和 的 〕 一 模
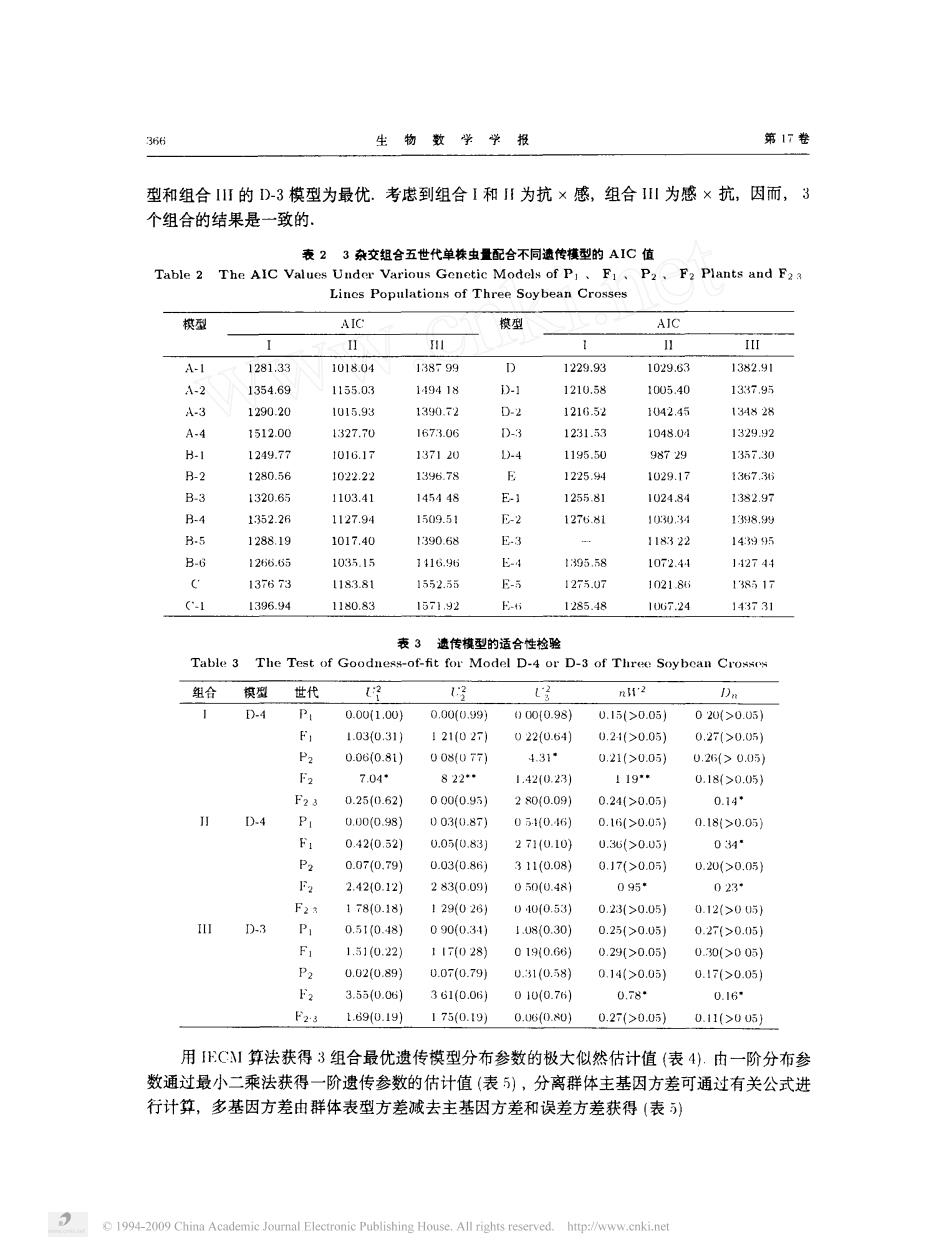
生物数学学报 第17卷 型和组合IⅡ的D-3模型为最优.考虑到组合1和Ⅱ为抗×感,组合川为感×抗,因而,3 个组合的结果是一致的 表23杂交超合五世代单株虫量配合不同遗传横型的AIC值 Table 2 The AIC P2, F2 Plants and F2 型 aIC 痕型 AIC I A.1 1281.33 101804 1338-99 D 1229.93 093 132.91 215 29 21 042 D-3 3 103.4 1024s E-2 127681 00 11832 1072.4 4274 13673 T183.8 552.3 E- 1275.0 102184 13851 1396.94 1180.83 157192 1285.48 106724 143行31 表3遗传模型的适合性检验 Table 3 The Test of Goodaess-of-fit for Model D-4 or D-3 of Three Soybean Crosse 组合筷 2 D-4 0.001.0U 0.00(0.s8) )000.98) 0.15(>0.05) 020(>0.U5】 1.030.31) 121027 0220.61) 0.21>0.05) 0,27>005 P 0.06(0.81) 005(077) 4.319 0.21(>0.05】 0.23>0.05 F2 7.04 822 1,420.23 119 0.18(>0.05】 F23 0.25(0.62) 000(0.95 200.09 0.21(>0.05 0.14° D4 P 0.000.98} 0030.87) 0510.46) 0.1i>0.0) 0.18>0.05 0.4210.52) 0.050.83 2710.10) 0.3>0.05) 04 P2 0.07(0.79) 0.030.85) 311(0.08) 0.17>0.05} 0.20(>0.05) F2 2.4210.12) 2830.091 0500.481 095* 023· 1780.18} 129026 430.53 0.2350051 0.12>005) D-3 P 0.510.48) 090(0.311 1.50.30} 0.25(>0051 0.271>0.051 F 1.510.22) 117(028) 0190.G8 0.29r>0.051 0200051 0.020.9} 0.070791 0.31(0.58 0.14(>0.05) 0.17(>0.051 3.55u051 361lD.05l 01uH0.7h 1690.19)1750.10)0.050.0 0.27(>0.05)0.11>005 用C1算法获得3组合最优遗传模型分布参数的极大似然估计值(表4).由一阶分布参 数通过最小二乘法获得一阶遗传参数的估计值(表5),分离群体主基因方差可通过有关公式进 行计算,多基因方差由群体表型方差减去主基因方差和误差方差获得(表) C 1994-2009 China Academie Journal Electronic Publishing House.All rights reserved.http://www.enki.net
生 物 数 学 学 报 第 卷 型和组合 的 一 模型为最优 考虑到组合 和 为抗 感 , 组合 为感 抗 , 因而 , 个组合的结果是一致的 表 杂交组合五世代单株虫 配合不同遗传模型的 值 毛 一 一 、 、 、 一 模型 模型 一 , 一 ·宝 鑫 一 弓 一 日 一 〔玉 飞 一 一 , 几 一 么 〕 一 一 卜二 礴 一 一 吝 一 〔 一 弓 一 一 一 二弓 一 二 二 一 今 ’ 一 苏 下苏 〔 几 、 一 弓 一 〔 名 表 遗传模型的适合性检验 一 一 · 一 一 、 · 一 组合 模型 一 一 一 世代 了 只 走省 一 夕 刀 , 刀 ‘ 〔 汪 鸿 污 , 刀 名 。 刀 〕 。 申 上 刀 名 刀 名 刀 , , , 二 刀 ·委〔 刀 二, , 石 ‘ 苏 ‘ 刀 ‘主 ‘ 污 · ·姜 〕 苏 弓 苏 〕 用 毛 算法获得 组合最优遗传模型分布参数的极大似然估计值 表 由一阶分布参 数通过最小二乘法获得 一阶遗传参数的估计值 表 , 分离群体主基因方差可通过有关公式进 行计算 , 多基 因方差 由群体表型方差减 去主基因方差和误差方差获得 表 动
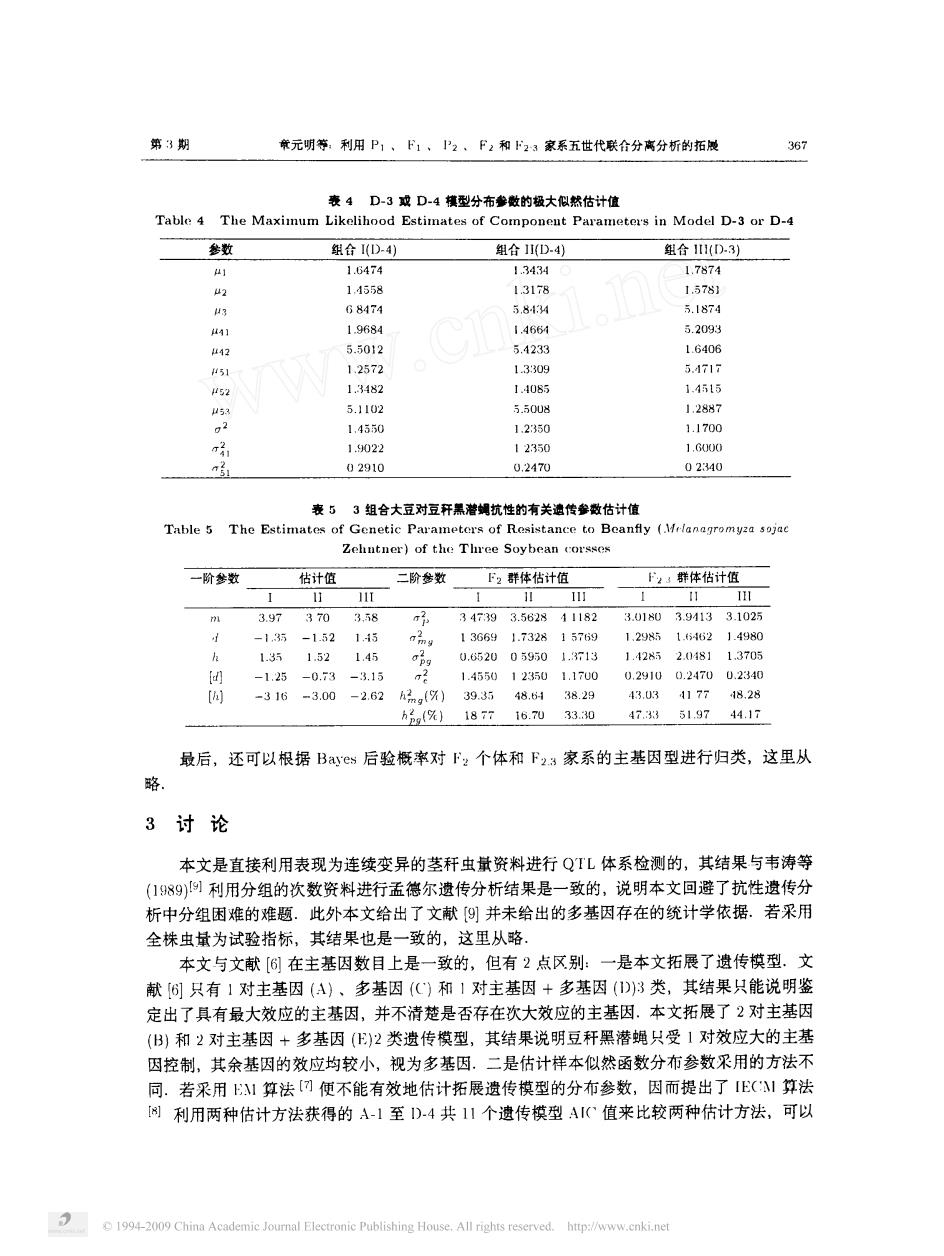
第3期 条元明等:利用P1,1、P2,F2和23家系五世代联合分离分析的拓楼 35 表4D-3成D4横型分布参数的极大似然估计值 Table 4 The Maximum Likelihood Estimates of Componeut Paramotors in Model D-3 or D-4 参 组合1D-4 合D 11558 G8474 5844 5.1574 19684 1466 5.209 4 5.5012 5.4238 1.6406 51 12572 52 14550 1250 11700 1.022 12350 1.G00 02910 0.2470 02340 表5 3组合大豆对豆开黑潜蝴抗性的有关速传参数估计值 Table 5 The Estimates Genetic Para etors of Res stance to Beanfly ( Zehutner)of the Three Soybeancor 一阶粉 估计值 下2群体估计低 ,群体估计值 11 11】 3.97 370 3.58 34793.562811182 3.0180394133102万 -135 115 136691.732 1576 1.298 162 1498 1.35 1 1.1 0.852005950 1.42 2n80234 300 05 h2()1877i6.703330 47.351.9744.17 最后,还可以根据Ba后验概率对F:个体和F23豪系的主基因型进行归类,这里从 3讨论 本文是直接利用表现为连续变异的茎秆虫量资料进行QTL体系检测的,其结果与韦涛等 (99)利用分组的次数资料进行孟德尔遗传分析结果是一致的,说明本文回避了抗性遗传分 析中分组困难的难题.此外本文给出了文献⑨并未给出的多基因存在的统计学依据。若采用 全株虫量为试验指标,其结果也是一致的,这里从略。 本文与文献[6在主基因数目上是一致的,但有2点区别: 一本文拓展了贵传模型.文 献⑤只有】对主基因(A)、多基因()和1对主基因+多基因(D)3类,其结果只能说明鉴 定出了具有最大效应的主基因,并不清楚是否存在次大效应的主基因.本文拓展了2对主基因 (B)和2对主基因+多基因()2类遗传模型,其结果说明豆秆黑潜蝇只受1对效应大的主基 因控制,其余基因的效应均较小,视为多基因。二是估计样本似然函数分布参数采用的方法不 同.若采用1算法[回便不能有效地估计拓展遗传模型的分布参数,因而提出了E(!算法 利用两种估计方法获得的A-1至D4共1个遗传模型A值来此较两种估计方法,可以 1-0 China Academie Electronie Publishing House.All rights reserved http://www.enki.net
第 期 章元明等 利用 、 、 八 、 和 几 家系五世代联合分离分析的拓展 表 一 成 一 棋型分布参嫩的极大似然估计值 一 一 、 一 · 一 一 参数 组合 一 组合 一 组合 一 闪内 阳阳限此 月 仃万一 。 写 。 置 勺 〕 二 污 几 】 〕 表 组合大豆对豆秆黑潜蝇抗性的有关遗传参数估计值 一 、 一 〔 人了, 、 夕 夕 , 一 一 《〕 , · 。 写 一阶参数 估计值 二阶参数 群体估计值 厂 群体估计值 【门 一 苏 苏 一 一 一 一 一 苏 乌 一 一 。 了 · 斋 , 。 。 么 。 钎 峪 。 下于 〕 石 汤 乌 异 丁 弓 污 之 二弓 蛋 〔 〕 们 人 、 、 沙 最后 , 还可以根据 ’ 后验概率对 个 体和 家系的主基因型进行 归类 , 这里从 略 讨 论 本文是直接利用表现为连续变异的茎秆虫量资料进行 体系检测 的 , 其结果 与韦涛等 始 利用分组的次数资料进行孟德尔遗传分析结果是一致的 , 说明本文 回避 了抗性遗传分 析中分组 困难的难题 此外本文给出了文献 〔 并未给出的多基因存在的统计学依据 若采用 全株虫量为试验指标 , 其结果也是一致的 , 这里从略 本文与文献 【 在主基因数 目上 是一致的 , 但有 点区别 一是本文拓展 了遗传模型 文 献 同 只有 对主基 因 川 、 多基 因 和 对主基因 多基 因 类 , 其结果只能说明鉴 定出了具有最大效应的主基因 , 并不清楚是否存在次大效应的主基 因 本文拓展了 对 主基 因 和 对主基 因 十 多基 因 类遗 传模型 , 其结果说明豆秆黑潜蝇 只受 对效应大的主基 因控制 , 其余基因的效应均较小 , 视为多基 因 二是估计样本似然函数分布参数采用的方法不 同 若采用 算法 便不能有效地估计拓 展遗传模型 的分布参数 , 因而提 出了 算法 利用两种估计方法获得 的 一 至 一 共 个遗传模型 值来 比较两种估计方法 , 可以