
第的原9期 6um西老衣林科技态学餐程自林科学E以 Valg 主基因-多基因混合遗传数量性状的 单性状选择模型 罗凤娟,董晓萌,袁志发,郭满才 《西北农林科挂大学理学院,陕西杨凌712100) [摘要]【日的】分别估计分离世代数量性状主基因-多基因混合遗传中的多基因效应方差和环境方差,为育 种工作者提供一种简单易行的单性状选择方法。【方法】利用正态分布的极限误差:将混合正态分布数据划分到多个 单一正态分布对应的风间,每一区间代表一种主基因型,采用有重复观测数据的单因家多元方差分析方法,分别估计 各主基因型间的主基因效应协方差阵,多基因效应协方差阵和环境协方差阵,然后结合程合正态分布中各成分分布 的比例,计算该数量性状的表型方装、透传方差,环境方差和遗传力等谁传参数,并进行实例分析。【结果】在相同选 择强度下,边传效率为110.3760%,较作为单一正态分布的普通数量性状选择效率提高了10.3760%。当选挥强度 =0,5时,遗传增益G5一28.41,【结论】应用建立的主基因多基因混合追传数量性状单性状选择模型计算,遗传效 有很大期高,表明该方法具有实用性 [关健词]数址性状,主基因多基因混合透传:AIC准则,EM算法:传地益:单性状迹择模型 [中图分类号]Q348:029 [文献标识码A [文章编号】1671-9387(2008)09-0190-0 Single character selective model of major gene and polygene mixed inheritance model of quantitative trait LUO Feng-juan,DONG Xiao-meng.YUAN Zhi-fa,GUO Man-cai (College of Science .Northwert A&F Univernty Yangling .712100.China) Abstract:[Objective]The study was done to estimate the variance of polygene effect and environmen- tal variance separately in the maior gene and polygene mixed inheritance model of quantitative traits from tion into the multiple sections which correspond single normal distribution,each section representing one major gene genotype,and the one-way analysis of variance of repeated data was applied to estimate the covariance matrix of major gene effect among major gene ger matrix of polyger e effect and environmental cova matrix.then the genetic p ceand heritability of the quanti tative trait,were calculated combining the proportion of the component distribution of the mixed norma distribution and an example was taken to analyse.[ResultI Under the same selection intensity,the genetic efficien cy was 110.3760%,it was improved by 10.3760%companred with the common quantitative trait which corre sponds single normal distribution.The genetic gain GS was 28.41 when the selection intensity was 0.5.IConclu sionUsing the single character selective model of major gene and polygene mixed inheritance model of 食经日的科学水全原空有特肉合经 万方数据
第36卷第9期 西北农林科技大学学报(自然科学版) V01.36 No.9 2008年9月 Journal of Northwest A8.F University(Nat.Sci.Ed.) Sep.2008 主基因一多基因混合遗传数量性状的 单性状选择模型 罗凤娟,董晓萌,袁志发,郭满才 (两北农林科技大学理学院,陕西杨凌712100) [摘 要]【日的】分别估计分离世代数量性状主基因一多基因混合遗传中的多基因效应方差和环境方差,为育 种工作者提供一种简单易行的单性状选择方法。【方法】利用正态分布的极限误差,将混合正态分布数据划分到多个 单一正态分布对应的区间,每一区间代表一种主基因型,采用有重复观测数据的单因素多元方差分析方法。分别估计 各主基因型问的主基因效应协方差阵、多基因效应协方差阵和环境协方差阵,然后结合混合正态分布中各成分分布 的比例,计箅该数量性状的表型方差、遗传方差、环境方差和遗传力等遗传参数,并进行实例分析。【结果】在相同选 择强度下,遗传效率为1i0.376 0%,较作为单一正态分布的普通数量性状选择效率提高了10.376 0%。当选择强度 净0.5时,遗传增益GS=28.41。【结论】应用建立的主基因一多基因混合遗传数量性状单性状选择模型计算,遗传效 牢有很大提高。表明该方法具有实用性。 [关键词]数量性状;主基因一多基因混合遗传;AIC准则;EM算法;遗传增益;单性状选择模型 [中图分类号]Q348;029 [文献标识码]A [文章编号]1671-9387(2008)09—0190—07 Single character selective modeI of major gene and polygene 一 ● 一 一一 mixed inheritance model of quantitative trait I。UO Feng—j uan,DONG Xiao—meng,YUAN Zhi—fa,GUO Man—cai (College of Science,Northwest A&F University,Yangling,Shaanxi 712100,China) Abstract:[Objective]The study was done to estimate the variance of polygene effect and environmen— tal variance separately in the major gene and polygene mixed inheritance model of quantitative traits from segregating generation and provide a simple single character selective method for breeding operators. [Method]This paper used normal distribution's limit error to plot out the data of mixed normal distribu— tion into the multiple sections which correspond single normal distribution,each section representing one major gene genotype,and the one-way analysis of variance of repeated data was applied to estimate the covariance matrix of major gene effect among major gene genotypes,covariance matrix of polygene effect and environmental covariance matrix,then the genetic parameters,namely the phenotypic variance,genetic variance and heritability of the quanti— tative trait,were calculated combining the proportion of the component distribution of the mixed normal distribution and an example was taken to analyse.[Result]Under the same selection intensity,the genetic efficien— cy was 1 10.376 0%,it was improved by 10.376 O%companred with the common quantitative trait which corre— sponds single normal distribution.The genetic gain GS was 28.41 when the selection intensity was 0.5.[Conclu— sion]Using the single character selective model of major gene and polygene mixed inheritance model of [收稿日期] f基金项目] [作者简介] [通讯作者] 2007—-09-·23 国家自然科学基金项目“空间协方差结构混合模型分析田间试验效果与技术”(30571072) 罗风娟(1982~).女.陕西宝鸡人,在读硕士,主要从事生物数学研究。E-mail:juanfengil@sina.corn 郭满才(1963一),男,陕西宝鸡人.教授,博士,主要从事农业应用数学研究。 万方数据

第9期 罗风娟等:主基因多基因混合遗传数量性状的单性状透择模型 191 this method. Key words:ch gene and polygene mixed inheritance AIC EM genetic gain single character selective model 动植物的许多重要经济性状,在分离世代往往 1 既具有可分组趋势,又存在组间界线模糊现象,这类 主基因-多基因混合遗传模型简介 性状在遗传上同时受少数主基因和大量微效基因控 假设主基因多基因混合遗传所控制的性状X 制,称之为主基因多基因混合遗传体系,如植物中 有x1共(>1)个主墓因型,表型向量 大豆的生育期、水稻的株高、小麦和大麦对叶锈病的 记为P-[xx,…,x]7,其遗传模型为) 抗性等,动物中影响羊排卵率的Booroola基因、家 P=m十g十emm十t十c十e. 禽中的矮基因等,在分离世代中,由微效多基因控 式中:m为中亲值向量:g为遗传效应向量,其协方 制的数量性状的表现型近似照从正态分布,而主基 差阵为e为环境效应向量,且e~N,(0,),其 因多基因混合遗传体系控制的性状表型呈现多蜂 中,为环境协方差阵为主基因效应向量,其协方 性,表现出多个分布混合的特征,对于此类性状的 差阵为c为多基因效应向量,且c~N,(0,) 研究,莫惠栋等1,姜长鉴等)、盖钩磁等幻和王建 其中为多基因效应协方差阵,c,e之间相互独 康等切分别建立了无主基因存在和主基因存在时 立,有,=,+2=十十,其中二,为表型协 的主基因多基因混合遗传数学模型,并对相应的参 方差 数进行了估计, 为了分别估计主基因效应协方差阵、多基因效 在分离世代数量性状主基因-多基因混合遗传 应协方差阵和环境协方差阵,本研究采用有重复的 模型分析中,前人的研究主要是基于无重复的完全 单因素多元方差分析,将主基因多基因混合遗传的 随机样本,只能估计主基因效应方差、多基因效 是个主基因型作为k个处理因素进行协方差阵分 应方差和环境方差之和,若要进一步估计多基因 析。因此,应将实际观测数据进行预处理,并对样本 效应方差 -d ,则必须加人不分离世代 体的主基因型进行划分,将每种主基因型作为单 P:和F:代估计环境方差。此外,在此类性状的 因素方差分析的 一个处理因素 遗传分析中,前人的研究主要是对遗传参数,遗传效 实际样本数据的预处理及样本个体 应的估计,以及对不同动植物的不同数量性状所属 2 的透传模型进行判别与分析,而未涉及选择问题,也 主基因型的划分 并未提出分离世代主基因多基因混合遗传的选挥 2.1 原样本数据的预处理 模型。针对以上两个问,本研究采用等重复观测 在实际观测中,设观测了包括所有主基因型的 样本试验设计方案,在单个分离世代中能分别估计 样本个体数为刀的全程样本,且每个样本重复视测 多基因效应方差和环境方差,并根据直接遗传进展 r次,因此实际观测数据是r行n列的包括所有主基 建立了主基因-多基因混合遗传的单性状选择模型, 因型的会样本信息。将实际观测数据从小到大排 以期为育种选择提供 种简便易行的选择方法 序,经过整理结果如表1所示 实际观测的数据表 Table 1 Data of practic I observation 样本个数Sample number me 平均值 往w1=1.2 12 个个体的第)次重复观满值 the 万方数据
第9期 罗凤娟等:主基因一多基因混合遗传数量性状的单性状选择模型 191 quantitative trait to calculate,the selection efficiency was higher,showing practicability of this method. Key words:quantitative character;major gene and polygene mixed inheritance;AIC;EM;genetic gain; single character selective model 动植物的许多重要经济性状,在分离世代往往 既具有可分组趋势,又存在组间界线模糊现象,这类 性状在遗传上同时受少数主基因和大量微效基因控 制,称之为主基因一多基因混合遗传体系,如植物中 大豆的生育期、水稻的株高、小麦和大麦对叶锈病的 抗性等,动物中影响羊排卵率的Booroola基因、家 禽中的矮基因等。在分离世代中,由微效多基因控 制的数量性状的表现型近似服从正态分布,而主基 因一多基因混合遗传体系控制的性状表型呈现多峰 性,表现出多个分布混合的特征。对于此类性状的 研究,莫惠栋等‘卜21、姜长鉴等‘引、盖钧镒等Ⅲ和王建 康等[5。]分别建立了无主基因存在和主基因存在时 的主基因一多基因混合遗传数学模型,并对相应的参 数进行了估计。 在分离世代数量性状主基因一多基因混合遗传 模型分析中,前人的研究主要是基于无重复的完全 随机样本,只能估计主基因效应方差口‰、多基因效 应方差和环境方差之和cr2,若要进一步估计多基因 效应方差盯2船=盯2一Z,则必须加入不分离世代P。, P。和F。代估计环境方差蠢。此外,在此类性状的 遗传分析中,前人的研究主要是对遗传参数、遗传效 应的估计,以及对不同动植物的不同数量性状所属 的遗传模型进行判别与分析,而未涉及选择问题,也 并未提出分离世代主基因一多基因混合遗传的选择 模型。针对以上两个问题,本研究采用等重复观测 样本试验设计方案,在单个分离世代中能分别估计 多基因效应方差和环境方差,并根据直接遗传进展 建立了主基因一多基因混合遗传的单性状选择模型, 以期为育种选择提供一种简便易行的选择方法。 1 主基因一多基因混合遗传模型简介 假设主基因一多基因混合遗传所控制的性状x 有z,,z:,…,z。共志(志>1)个主基因型,表型向量 记为P一[zl,z2,…,z1]丁,其遗传模型为[7]: P=m+g+P=m+t+f+e。 式中:优为中亲值向量;g为遗传效应向量,其协方 差阵为三。;e为环境效应向量,且P~N。(O,五),其 中五为环境协方差阵;t为主基因效应向量,其协方 差阵为五;f为多基因效应向量,且f~N。(0,五), 其中五为多基因效应协方差阵;t,c,e之间相互独 立,有昌=五+厄=五+五+五,其中耳为表型协 方差阵。 为了分别估计主基因效应协方差阵、多基因效 应协方差阵和环境协方差阵,本研究采用有重复的 单因素多元方差分析,将主基因一多基因混合遗传的 志个主基因型作为惫个处理因素进行协方差阵分 析。因此,应将实际观测数据进行预处理,并对样本 个体的主基因型进行划分,将每种主基因型作为单 因素方差分析的一个处理因素。 2实际样本数据的预处理及样本个体 主基因型的划分 2.1原样本数据的预处理 在实际观测中,设观测了包括所有主基因型的 样本个体数为行的全程样本,且每个样本重复观测 r次,因此实际观测数据是r行靠列的包括所有主基 因型的全样本信息。将实际观测数据从小到大排 序,经过整理,结果如表1所示。 表1实际观测的数据表 Table 1 Data of practical observation 1 J r 平均值Average .Zil :● 工l』 :● Z} 一 Z. Xal :● Z咐 :● 工∥ 一 Tn 注:z。(f_1.2.…。ntj一1。2。…。r)表示第i个个体的第j次重复观测值;五(i=1,2,…,n)表示第i个个体的平均观测值。 Note:z”(f=1,2·…,n;j=1。2,…,r)isthe J times repeatedmeasure value oftheiindividual;蟊(i=1,2,….月)isthe averageobservation value of the individual. 万方数据
百北农林科技大学学报(自然科学版) 第36卷 该数量性状是主基因多基因混合遗传,其表型 其中i=1,2,…,k,则各成分分布的均值以(i=1,2, 观测值呈现多峰性,表现为多个正态分布的混合,故 …,)的3区间为[一34,十3,]。因此,可将各 混合分布理论来估计参数进行主基因型的划分. 观测个体的均值,(i=1,2 2.2 3 混合分布参数的估计 3g](=1,2,,)分别划分到相应的k个区间中, 混合分布中所包含成分分布的个数k利用 进而将其对应的每组观测值x。(i=1,2,,:三 Akaike提出的最大摘信息准则(AIC))来估计,混 1,2,…,r)划分到对应的区间中,即相应的主基因型 合分布中其他参数,即各成分分布的均值出、权重 ,,中。若其不干某区间,将理利个 和方差(=1,2,…,k),采用EM算法 估计 体在此区对应的主基因型中的观测数据记为0, 因为样本的每组重复观测值间存在一定误差 这样就得到表2数据形式, 同一个体的不同重复观测值可能划分到不同的区 例如:若第1个样本到第p(p<m)个样本的均 间,即属于不同的主基因型,这与实际情况不符,故 值在[1一3,4十3,]区间,则判定这些样本属于 参数的估计用其均值x,工。, ,,即一组全样本 混合分布中的第1个成分分布,其主基因型为 信息进行计算 则其余样本的观 数在主基因型中记为0,可认 2,3 观测样本个体主基因型的划分 为这些样本在基因型为x,时观测不到:其他样本个 假设测量值xN(u,2),则由正态分布的极限 体主基因型的划分与此类似, 误差山可知,x落在区间Cu一3g,a十3c]外的概率非 对每个个体的重复观测值进行主基因型划分 常小,因此由此极限误差划分各观测个体所属的区 后,实际观测数据可整理为表2的形式。这种观测 间,即对应的主基因型类别,信息损失较小 设计可按重复中有重复的单因素完全随机设计进行 设混合分布的成分分布个数为k,即有k种主 离差阵分析。 基因型:各成分分布的均值和方差分别为出和, 表2等重复的单团来随机试验数细 Table 2 Data of the single element tandom experiment with eaual repetition number 样本个数S T T 生:n(-1,2,…,k=1,2,,=1,2,…,r)为第)个观测个体的第1次重复观测值的第:个主基因型值。 3主基因和多基因存在的检验 判定主基因的存在,如果k=1,则说明无主基因存 在:如果k≥2,则说明有主基因存在。但具体的主 3.1主基因存在的检验 基因座位点之间的相互作用,如加性效应,完全显 对于主基因多基因混合遗传的数量性状来说, 性、部分显性等还需进行进一步的似然比假设检验, 根据其表型混合分布中成分分布个数表的大小 可以 才能作出相应推新,本文不加以详述 万方数据
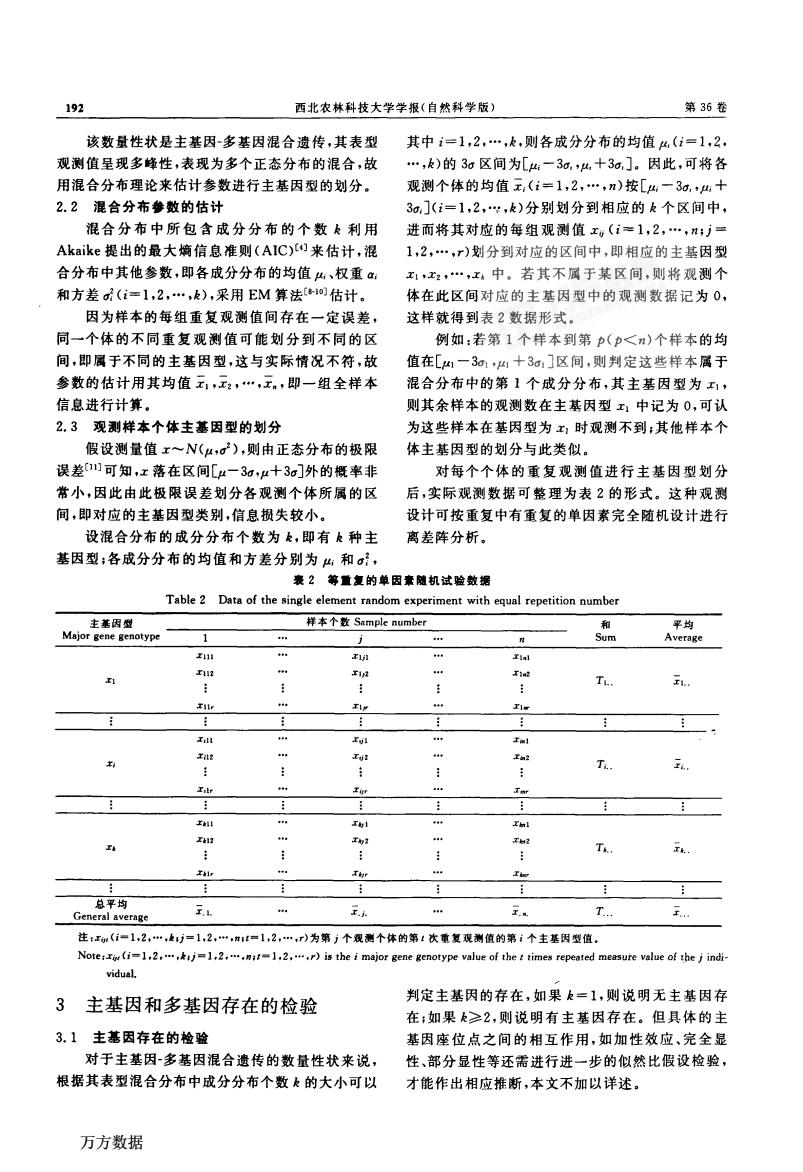
192 西北农林科技大学学报(自然科学版) 第36卷 该数量性状是主基因一多基因混合遗传,其表型 观测值呈现多峰性,表现为多个正态分布的混合,故 用混合分布理论来估计参数进行主基因型的划分。 2.2混合分布参数的估计 混合分布中所包含成分分布的个数忌利用 Akaike提出的最大熵信息准则(AIC)[4]来估计,混 合分布中其他参数,即各成分分布的均值胁、权重口f 和方差盯;(i=1,2'..·,愚),采用EM算法[8。0]估计。 因为样本的每组重复观测值间存在一定误差, 同一个体的不同重复观测值可能划分到不同的区 间。即属于不同的主基因型,这与实际情况不符,故 参数的估计用其均值;。,;:,…,;。,即一组全样本 信息进行计算。 2。3 观测样本个体主基因型的划分 假设测量值z~N(岸,口2),则由正态分布的极限 误差[111可知,z落在区间h一3a,P+3司外的概率非 常小,因此由此极限误差划分各观测个体所属的区 间,即对应的主基因型类别,信息损失较小。 设混合分布的成分分布个数为忌,即有惫种主 基因型;各成分分布的均值和方差分别为“;和口;, 其中i=1,2,…,k,则各成分分布的均值雎(i=1,2。 …,志)的3口区间为[卢i一3a,,P。+30,]。因此,可将各 观测个体的均值至;(i=1,2,…,咒)按[户。一3a,,户j+ 3巩](i一1,2'..f,足)分别划分到相应的志个区间中, 进而将其对应的每组观测值zⅡ(i=1,2,…,”;歹= 1,2,…,r)划分到对应的区间中,即相应的主基因型 z。,z。,…,z。中。若其不属于某区间,则将观测个 体在此区间对应的主基因型中的观测数据记为0, 这样就得到表2数据形式。 例如:若第1个样本到第P(户<以)个样本的均 值在[卢。一30。,户。+30,]区间,则判定这些样本属于 混合分布中的第1个成分分布,其主基因型为z。, 则其余样本的观测数在主基因型z。中记为0,可认 为这些样本在基因型为z,时观测不到;其他样本个 体主基因型的划分与此类似。 对每个个体的重复观测值进行主基因型划分 后,实际观测数据可整理为表2的形式。这种观测 设计可按重复中有重复的单因素完全随机设计进行 离差阵分析。 裹2等t复的单因素随机试验数据 Table 2 Data of the single element random experiment with equal repetition number 注lo咖(f一1,2·…,ItIj=1·2’-.’·”lf21,2,…,r)为第j个观测个体的第t次重复观测值的第i个主基因型值。 Note:zo,(f一1t2,…,量Ij21,2,…,t/ft=1。2.…,r)is the i major gene genotype vaJtle of the t times repeated measure Va]Lie of the J indi— viduai. , 3主基因和多基因存在的检验 翟盖篙焉盖等;兰i:罂罢?蚕妻惹是至 3.1主基因存在的检验 基因座位点之间的相互作用,如加性效应、完全显 对于主基因一多基因混合遗传的数量性状来说, 性、部分显性等还需进行进一步的似然比假设检验, 根据其表型混合分布中成分分布个数是的大小可以 才能作出相应推断,本文不加以详述。 万方数据

第9期 罗凤娟等:主基因多基因混合传数量性状的单性状选择模型 193 3.2多基因存在的检验 其中为环境协方差阵 如果主基因存在,可以将主基因的变异从总的 以上参数的最小二乘估计分别为: 表型亦异中分离出来,但是仍需确定主基因之外的 变异是来自多基因,环境、或是两者共同作用的结 果,即应对多基因的存在进行鉴定,假设混合分布 a=x.-x,月。=x.-x.,e=xm一元. 的成分分布个数为k,观则样本个数为n,则样本的 4,2协方差阵的分解 似然函数为: 对于每个观测值有重复的总离差阵W,可分解 L(p)=fp()=IIf () 为主基因型间的离差阵即主基因效应离差阵L,主 基因型内的离差阵即多基因效应离差阵L:和随机 构造零假设H。:=(即不存在多基因),其 误差的离差阵即环境离差阵L,3部分切, 中j=1,2,…,k,备择假设H。:d>d(即有多基因 生基因型间的离差阵为 存在),其中=1,2,…,k,且互不相等。通过计 65:…6 算两种假设下似然函数最大值L,和L,构造出似 然比统计量 L=nXrx λ=2[1ogL.一logL.Jy2(k-1) 式中:L.=i2元f,(z,d),L。=i2xf,(i =(i.-x) ,),进而对上述假设进行显著性检验。若A> 其中5=6=(G.-五-)(位.-云-). X(k一1),则拒绝原假设,说明在显著水平。下有多 j=1,2,…,k,≠j 基因存在,即除主基因之外的变异是多基因和环境 主基因型内的离差阵即多基因效应离差阵为: 共同作用的结果,香则,接受原假设,在显著水平。 「:52…ia1 下无多基因存在,即除主基因之外的变异只是环境 作用的结果。 4 主基因-多基因混合遗传的方差分 5,折… 6=G-王 4.1方差分析模型的建立 其中 设 是主基因型为工,的第j个观到个体的第 :次重复观测值,主基因型工的均值为:,第j个观 i,p=1,2,…,k,i≠p 测值的主效应为B,,x。的第1次重复观测的随机误 随机误差的离差阵即环境离差阵为: 差为ew,则方差分析的统计模型为, x=十风十e :… =1,2,…,k; j=1,2,",n …」 t=1,2,…,r, -22-八 主基因型五1,x2,…,工,的理论平均值分别为1性, …以其均值=产.把离差a,=4一(i=1, 其中5=片=之2(xn一云.)(红m一王w.) i,p=1,2,,k,i≠ 2,…,k)称为主基因型工的主效应,则有: u+a.+8,+em L,L:和L,的自由度分别为: i=1,2 =1,2 f=k-1,f=k(m-1),f=kn(r-1)1 在这个核型中间相豆维立,日均复从从0。 1.2 L,L,和L,的均方离差阵为: ),其中为主基因型间的主基因效应协方差阵, s,-点 8,相互独立,且均服从N,(0,E),其中为多基因 效应协方差阵:知为随机误差,且均服从N,(0,3), SP.-1 万方数据
第9期 罗凤娟等:主基因一多基因混合遗传数量性状的单性状选择模型 193 3.2 多基因存在的检验 如果主基因存在,可以将主基因的变异从总的 表型变异中分离出来,但是仍需确定主基因之外的 变异是来自多基因、环境、或是两者共同作用的结 果,即应对多基因的存在进行鉴定。假设混合分布 的成分分布个数为忌,观测样本个数为起,则样本的 似然函数为: n n ^ L(9’亍旦户(zr;妒)=。I。I。,E;。,r,f,(置;胁,考)。 l=I l-工,=J 构造零假设H。:Z—O,,2(即不存在多基因),其 中歹一1,2,…,k;备择假设H。:Z>Z(即有多基因 存在),其中J=1,2,…,k,且Z互不相等。通过计 算丽种假设下似然函数最大值L。和L。,构造出似 然比统计量: 3,=2[109L。一logLq]~;【2(k--1)。 n ● ^ ^ 式中:L。=量蚤码^(zr;膨,Z),Lo=卫。njfj(zz; l=l,一l l=j,;l 弘i,Z),进而对上述假设进行显著性检验。若A> z:(是一1),则拒绝原假设,说明在显著水平口下有多 基因存在,即除主基因之外的变异是多基因和环境 共同作用的结果;否则,接受原假设,在显著水平口 下无多基因存在,即除主基因之外的变异只是环境 作用的结果。 4 主基因一多基因混合遗传的方差分 析 4.1 方差分析模型的建立 设z卿是主基因型为z;的第.『个观测个体的第 t次重复观测值,主基因型z;的均值为弘;,第J个观 测值的主效应为风,zo的第t次重复观测的随机误 差为e¨则方差分析的统计模型为m。131: z咖=lui+岛+e咖, f一1,2,…,k o J一1,2,…,咒‘ £=1,2,…,,.。 主基因型z,,z。,…,z。的理论平均值分别为卢。,户z, …,胁,其均值产=÷至∥i。把离差oi2肛-l_(i=1, 2,…,曼)称为主基因型霸的主效应,则有: zⅡt=弘+口{+岛+£班, i=1,2,…,志;i=1,2,…,以,£=1,2,…,,.。 在这个模型中,口。问相互独立,且均服从M(0, 五),其中蜀为主基因型间的主基因效应协方差阵; 岛相互独立,且均服从N。(o,嚣),其中嚣为多基因 效应协方差阵;e们为随机误差,且均服从Nt(0,嚣), 其中E为环境协方差阵。 以上参数的最小二乘估计分别为: ^ 一 ^ 一 ^ 一 产2z…’肛0 2z口.,产i 221..’ ^ 一 一 ^ 一 一 ^ 一 口f2zf..一z…,m 2z#.--X1..’e咖2z扣一z口.. 4.2协方差阵的分解 对于每个观测值有重复的总离差阵W,可分解 为主基因型间的离差阵即主基因效应离差阵Lf,主 基因型内的离差阵即多基因效应离差阵LI和随机 误差的离差阵即环境离差阵L。3部分[1 2。13]。 主基因型间的离差阵为: 其中 LI=挖×r× ‰ 器2 巧1 Z;2 改l Z:2 … ‰ … 改 i i … 纥 俄=(;-一五)2 其中{%=缘=(;。一;…)(三“一;。.)。 【i,J=1,2,…,七,i=fij 。 主基因型内的离差阵即多基因效应离差阵为: L。=,.× 巧l 巧2 巧l Z;2 Z:1 Z:l …Z{^ … 圾 : : ● ● … 段 ;=∑(毛.一瓦)2 J-l - r ;=£0=五(至#.一三i..)(三厨.一;^.)· ,p一1,2,…,k,i≠P 随机误差的离差阵即环境离差阵为: L。。 窍l 毋2 巧l % Z:l Z:2 … Z:。 … Z缸 : : ● ● … & 俺=∑∑(z咖一毛.)2 j叠It一1 ’ 其中{岛一住=壹耋(z班一;d.)(z螂一三何.)。 I’ ’ 』蕾It—l 。 。 一 一 【i,p=l,2,…,志,i=fip L、L和L。的自由度分别为: ,u=k--1,fk=k(n--、、),fh=kn(r--1、)I LI、L和L.的均方离差阵为t SP,=k皂l, 皿=丽‰, 万方数据

西北农林科技大学学报《自然科学饭) 第36叁 SP.-in(-1 ESP.=E,+rZ.. ESP,=C 各均方的期值望分别为 离差阵分析模式见表3。 ESP,=E,+r.+nrE. 表3主基因型间离差阵的分析模式 Table 3 Covariance matrix analysis among the major gene genotypes 变异来原 度 离 均方惠五环 期型均方离麦科 主因型 or gene genotypes k-1 SP. k(m-1) L sP. E+ SP. 总变异Total 当原假设H1:=0,H:E=0成立时,L,L 为各主基因型间的表型协方差阵。 主基因遗传方差为。=a',a多基因遗传方 kn(r- 差为g=aTEa:环境方差为a=aT∑.a:遗传方若 w,(-1,), 为a2,=aTΣa=aT(.十)a:数量性状的表型方差 为=a'g,a=a'(,+.)a=ar(++)a 主因速传力为一多基因传力为配 A(f.). L 且根据Bartlett的研究结果,有 主因与多图传为即广义传方为 V,=-[,+,-(k+f+1)/2]lnA,x() V,=-Cf.+f.-(k+f.+1)/2]ln△ =十妮环境遗传力为:成好= 由样本计算V,和V,若V,≤(,)且V,≤ 遗传增益GS为:GS=ia,h,其中i为选择强 X(kf),则接受Ho和Ha,否则拒绝原假设。 度,可,为表型方差,h为遗传力),对主基因-多基 V,和V.均显若时,可估计参数2、三。和2,即: 因混合遗传控制的数量性状,其选择模型可用G 表示为 ∑.=SP,, GS-iagh-iaxhito 2=(sP.-sP,), 在同一选择强度下,遗传效率 2-R,-sP,) 5主基因-多基因混合遗传体系的单 式中:%,是主基因多基因混合遗传时的表型方差 性状选择模型 是将此数量性状作为普适数量性状,即表塑值服 从单一正态分布时的方差。 根据文献[810]的方法,计算出混合分布中成 由以上分析,对于主基因多基因混合遗传的数 分分布个数为k,每个成分分布的权重分别为a:, 量性状的不同个体群,在一定选择强度下,将其遗传 a2,…,a4,且之a,=1,则该数量性状X由k种主基 增益按大小顺序排序,选择遗传增益较大者即可 因型控制,分别记为,…,并有 Xal+a,++a=ap 6实例分析 式中,=「a ,],P=[z:x.. 根据盖钩做等!对骨绿豆×上海红芒早下:世 因此,X的表型方差为 代不同个体开花期的观测及计算结果,用Matlab中 a: 的normrnd随机产生两组数据,每组数据各有 20 a: 个,均包含两个具有不问均值,相同方差的正态分 dw=[a1,a…,a], =aEa,其中, 布,两个正态分布的均值分别为山=3.18,出 a 39.5,方差为==5.35,且混合分布中两个成分 万方数据
西北农林科技大学学报(自然科学版) 第36卷 SPe赢%; 各均方的期值望分别为: ESP,=五+历。+以垤。, EsPc一∑|+rr,c, ESP。=邑。 离差阵分析模式见表3。 表3主基因型闻离差阵的分析模式 Table 3 Covariance matrix analysis among the major gene genotypes 当原假设H…五=0,H。。:最=0成立时,L,L。 与L。相互独立,且L~W。lien(r一1),五],fe一 足以(r一1);L。~w女[忌(咒一1),五],正=k(n--1);Ll~ w^(志一1,五),丘=志一1。 由Wilks统计量可知m]: 凡一Ⅱ:与生1~A(志,工,^), A,=砸士擎旨~A(点,工,工), 且根据Bartlett的研究结果,有 V。=-EL+f,一(是+^+1)/2]lnA。~Z2(惫^), V,=-[L+L一(k+fi+1)/2]lnA,~x2(走丘)。 由样本计算V。和U,若V。≤菇(惫^)且V≤ 瑶(忌f),则接受H。·和H。z,否则拒绝原假设。当 V,和V。均显著时,可估计参数邑、五和三。,即: E=SP。, h 1 五=二(SPc-SP。), A 1 五=二(SP。一S只)。 5 主基因一多基因混合遗传体系的单 性状选择模型 根据文献[8一103的方法,计算出混合分布中成 分分布个数为k,每个成分分布的权重分别为口,, ^ 口:,…,a。,且∑ni=1,则该数量性状X由惫种主基 因型控制,分别记为∞,z。,…,z。,并有 X=a1Xl+口222+…+口女z^一口7P。 式中:a=[口1,n2,…,口女]1’,p_--rxl,z2,…,z^]丁。 因此,X的表型方差为: 矗=[口1,口2,…。口I]蜀 nl n2 :● 口^ =口您ra,其中三, 为各主基因型间的表型协方差阵。 主基因遗传方差为盯免=n您,口;多基因遗传方 差为以=口72。a;环境方差为盯乞一口72。a;遗传方差 为盯k—n7皇。a—n7(五+矗)n;数量性状的表型方差 为疗乙一n7三p口=口7(置+邑)口=口丁(五+嚣+邑)口。 主基因遗传力为,l;=2仃7k-;多基因遗传力为,l?= 宰;主基因与多基因遗传力即广义遗传力为:h2= 争=肜+瑶;环境遗传力为:^;=堕。 o却 Umx2P 遗传增益GS为:GS=ia。h 2,其中i为选择强 度,郇为表型方差,h2为遗传力n4]。对主基因一多基 因混合遗传控制的数量性状,其选择模型可用G, 表示为。 GS=iaoh 2=iaxph(2件d。 在同一选择强度下,遗传效率 叩=笔净。 式中:盯x。是主基因一多基因混合遗传时的表型方差, 如是将此数量性状作为普通数量性状,即表型值服 从单一正态分布时的方差。 . 由以上分析,对于主基因一多基因混合遗传的数 量性状的不同个体群,在一定选择强度下,将其遗传 增益按大小顺序排序,选择遗传增益较大者即可。 6 实例分析 根据盖钧镒等…对骨绿豆×上海红芒早F。世 代不同个体开花期的观测及计算结果,用Matlab中 的normrnd随机产生两组数据,每组数据各有200 个,均包含两个具有不同均值、相同方差的正态分 布,两个正态分布的均值分别为∥。=3.18,Pz= 39.5,方差为盯}一击:5.35,且混合分布中两个成分 万方数据