
Journal of 生物数学学报2001,16(3):341-347 Biomathematics 非平衡群体基因变异测量的Shannon信息量方法 郭满才宋世德周静芋袁志发 (西北农林科技大学生命科学学院。陕酒杨液71210) 物要:在Shannon告怎重的益出上,对非平街群体建立了年体基因型相对信怎量S1G. 纯合体相对信息量S(G、杂合体和对信息量SHG)的鞭念,并《子它们以遭传学惠义.与基 一度」和基多样度D选了理论比权,结采明,二者在数量规上有很好的一此性 应又无构时做立的指标件系,且各构时雪8量还有新的内话。S©)就能表丛泰因定异,又镜 反映基日型水平上的道传变异,S(G)主要反块纯合体的违传变养,S(G)主要反映杂合体的 遗传变异。各相对信怎量既可反唤年保的造传变异位度,又能比枝不网位点问的通传变异很度。 关键词非平衡年体:Shanne0n信息量,基因一其度:基园多样定:年体基因型任怎量 中图分类号:S813.1MR分类号:20B30;92D20 文献标识码:A 文童编号:1001-96262001103034107 如何定量地描述非平衡群体的基因变异,N刊认为在非随机交配群体中,虽然杂合度与 群体内杂合体的颜率无关,不过它仍然是一个群体内基因变异的理想尺度,可以适用于任何生 物,无论是自体受精生物还是异体受精生物;是单倍体还是多倍体.并建议对这些生物,把杂 合度H改称为“基因多样度”,纯合度J改称为“基因一致度”, Weir网在论述基因多样性时 也沿用同样的指标.。但实际上,对于非平衡群体,这种描述只利用了基因库须率而没有利用基 因型领率.1998年袁志发等提出用相对Shannon信息量描述平衡弹体的基因变异问,并赋 予它们以遗传学意义.本文拟研究非平衡群体基因变异的Shannon信息量测量方法,并与基 因多样度进行比较研究,对定量描述群体的基因变异提供-一种新的方法,以使Sha1o加信息其 方法得到更好的应用. 基因多样度D)及其性质 设复等位基因位点A为 (A1,A2,Ax)=(B,P,,Px) 其中乃为A,的额率,R≥0,且公P=1.其对应的群体在理论上有无穷多个,不失一般 安精日期:1999-08-15 作者简介:郭情才(1963-),男。陕西宝鸡人,西北农林科技大学生印科学学院碳士 万方数据
生物数学学报2001,16f31:341 347 JournaI of Biomathematics 非平衡群体基因变异测量的shannon信息量方法 郭满才 宋世德 周静芋 袁志发 (西北农林科技大学生命科学学院,陕西杨陵7121001 摘要:在shannon信息量的基础上,对非平衡群体建立了群体基因型相对信息量s。(G). 纯舍体相对信息量sj(G)、杂合体相对信息量s备(G)的概念,并赋予它们以遗传学意义与基 因一致度J和基因多样度D进行了理论比较,结果表明,二者在数量规律上有很好的一致性, 但又是相对独立的指标体系,且各相对信息量还有新的内涵. S。(G)既能表征基因变异,卫能 反映基因型水平上的遗传变异,sj(G)主要反映纯合体的遗传变异,s岛(G)主要反映杂合体的 遗传变异各相对信息量既可反映群体的遗传变异程度,又能比较不同位点问的遗传变异程度. 关键词:非平衡群体;shannon信息量;基因一韭度;基因多样度;群体基因型信息量 中圈分类号:S813 l MR分类号:20830;92D20 文献标识码:A 文章编号:lool一9626(2001)03一034l—07 如何定量地描述非平衡群体的基因变异,Nc·【1】认为在非随机交配群体中,虽然杂合度与 群体内杂合体的频率无关,不过它仍然是一个群体内基因变异的理想尺度,可以适用于任何生 物,无论是自体受精生物还是异体受精生物;是单倍体还是多倍体.并建议对这些生物,把杂 合度Ⅳ改称为“基因多样度”,纯合度,改称为“基因一致度”.weir【4】在论述基因多样性时 也沿用同样的指标.但实际上,对于非平衡群体,这种描述只利用了基因库频率而没有利用基 因型频率. 1998年袁志发等提出用相对shannon信息量描述平衡群体的基因变异【5】,并赋 予它们以遗传学意义.本文拟研究非平衡群体基因变异的shannon信息量测量方法,并与基 因多样度进行比较研究,对定量描述群体的基因变异提供一种新的方法,以使sha,·n。n信息鼍 方法得到更好的应用. 1 基因多样度D【-】及其性质 设复等位基因位点A为 (A】,A2 ,J4Ⅳ)=(|DI,P2, ,PⅣ K 其中只为J4。的频率,只≥o,且∑只=1其对应的群体在理论上有无穷多个,不失一般 z=1 收稿日期:1999—08—15 作者简介:郭清才(1963一),男,陕西宝鸡人,西北农林科技大学生命科学学院副教授.硕士 万方数据

342 生物数学学报 第16卷 性,设它们为 (AA,A2A..AKAK:AA2.A1A3Ag-1AK) =(D1,D2,,DK,2,H13,…,HK-,K) 2② 其中纯合基因型AA有K个,频率为D,杂合基因型A4任<)有K(K-1/2个,频 本为,显然言D+=1共有基因型K(K+/2种 基因库(1)或群体(2)的基因一致度J和基因多样度D分别定义为 J=∑.D=1- (3) 其性质为 0sDsK1 当B之一等于1而其余均为0时,有hm=1,D=0:当乃均等于时,有an= 三D=K1显然.基因一致度J与多样度D分别是以平衡群体的纯合体频率与杂合 体频率为代表来度量具有同一基因库的任一群体的基因变异, 2非平衡群体相对信息量及其性质 当群体(②)不平衡时,其Shannon信息量定义为 O=-Dh+∑aH 群体的纯合体信息量S,(G)和杂合体信息量SH(G)分别定义为 S(C)=D.In D.5n(G)=-Hgla (6 则有 0≤SG=Sg+Sm1GshK+卫 (0 2 当群体中只有一种基因定时SG=0:当优+少种基因型颜米相等,且均为不可 时SGa=hK+,此时 sg=子h,sq- 2 由于(②的不平衡性,5SG)与S(以及SG的最大值不在同一点取得,结论如下(证明 当K≥3时 万方数据
万方数据

第3期 郭清才等,丰平衡群体落因变异测魔的Shannon信息基方法 343 其中当D皆等于京时5Gmm=hK:当风,皆等于-可时,5n(G= nK5-】0,或之一为1,其余为0时,它们均取最小值0 当k=2时 0≤SG)s, 0sSmG)≤ 其中当D=h=时,SGmw=是;当i=时,Su(G)a=是当D,D之-为 1,另-个为0时(Gmm=0,当H12=1时,SH(Gmn=0, S'(G,S(G)和Sa(G分别为群体的相对信息量,纯合体相对信息量和杂合体相对 信息量,则k≥3时 SJG) ≤G=b-n (10 (11) S(G) 0(G)-(G)+S(G)sI (12 当=2时,由(),(9)可得与(0)-(12类似的式子. SG的遗传学意义为群体(②的不背定性大小,S(G)表示纯合体的不肯定性大小, S(G)为群体的不肯定性程度,5分(G)为纯合体的不肯定性程度,即占最大可能不肯定性的比 例.SH(G与SH(G)可仿此解释. 对于具有多个位点的非平衡群体,可建立相应的平均信息最与平均相对信息量 3模拟结果与分析 对上述理论结果,在长=2时进行计算机模拟。A1的初始领率为0.0,步长0.1,终止频 率10,基因型率步长为0.05时模拟了511个群体A的初始额率0.00,步长0.01,头 止频率0.50,基因型频率步长为0.005 时模拟了2601个群体.用豆,S(G),Sa(G与S(G)分 别表示具有同一基因库的所有模拟群体杂合体频率 ,的平均值,纯合体相对信息#G 的平均值,杂合体相对信息量Sa(G的平均值以及相对信息量S'G)的 平均值。模拟结果与 理论结果完全相符(如最大值、最小值、最大值点、最小值点等),对模拟结果进行统计 得出如下有意义的结 (部 分数据见表1-表5,表4、表5为表1数据计算结果.其余略 )同一基因库的每一模拟群体,只要三种基因型的频率均不小于0.03,则其S(G,G。 5SG分别与该库的S(©,S(G,S#(G)差异不显著 2)D与月的关系为:当A1的颗率在0.0,0.061,0.47,0.531,0.94,1.00范围内时,二者差 异不显著。对其它基因库,二者有显著或极显著的差异,且D与月相比偏大: 3)D与(G)的关系为 当A1在0.00,0.03]及0.97,1.00范围内时,二者差异不显著。 对其它基因库,二者差异显著或极显著,且D与S(G)相比偏小.户与S(G)有与之完全类 似的性质. 万方数据
第3期 郭满才等;非平衡群体基因变异测量的shannon信息量方法 其中当。,皆等于去时s,(G)m。。=lnK;当皿,皆等于志时, sH(G)…= ln竺呸÷旦D:或爿玎之一为1,其余为。时,它们均取最小值。 当^=2时 o≤s,(G)s i o s sH(G)曼÷ 其中当D。=仍=÷时,曲(G)…=;;当Jv-z=:时,跏(G)。ax=:当D·,Dz之一为 j,另一个为。时曲(G)m。。=o,当Ⅳ12=l时,sH(G)删。=o 定义s’(G),彤(G)和s0(G)分别为群体的相对信息量,纯合体相对信息量和杂合体相对 信息量,则☆≥3时 ㈣”,2器s尚 Ⅲ拍,=器墨牟 唧悱尚划G)+郫)<l f10) (12) 当^=2时,由(7),(9)可得与(1【))一(12)类似的式子. s(G)的遗传学意义为群体(2)的不肯定性大小, s,(G)表示纯合体的不肯定性大小. s7(G)为群体的不肯定性程度,s,(G)为纯合体的不肯定性程度,即占最大可能不肯定性的比 例. sH(G)与s鲁(G)可仿此解释. 对于具有多个位点的非平衡群体,可建立相应的平均信息量与平均相对信息量. 3模拟结果与分析 对上述理论结果,在k=2时进行计算机模拟.A,的初始频率为0 o,步长o 1,终止频 率l O,基因型频率步长为0 005时模拟了511个群体.Al的初始频率0 00,步长o 01,终 止频率ojo,基因型频率步长为o 005时模拟了2601个群体.用H,$(G),s备(G)与s7(G)分 别表示具有同一基因库的所有模拟群体杂合体频率Ⅳ12的平均值,纯合体相对信息量昌(G) 的平均值,杂合体相对信息蹙50(G)的平均值以及相对信息量s7(G)的平均值.模拟结果与 理论结果完全相符(如最大值、最小值、最大值点、最小值点等)对模拟结果进行统计分析, 得出如下有意义的结果(部分数据见表1一表5,表4、表5为表L数据计算结果.其余略) 1)同一基因库的每一模拟群体,只要三种基因型的频率均不小于o 03,则其s’(G),昌(G) s二(G)分别与该库的s7(q,乃(G),%(G)差异不显著. 2)D与曰的关系为:当Al的频率在fo 00,o 06],[o 47,o 5 3】,[o 94,1.00]范围内时,二者差 异不显著.对其它基因库,二者有显著或极显著的差异,且D与H相比偏大. 3)D与雪’(G)的关系为:当A。在(0 oo,o 03]及[o 97:l 00]范围内时,二者差异不显著. 对其它基因库,二者差异显著或极显著,且D与s7(G)相比偏小. H与s 7(G)有与之完全类 似的性质. 万方数据
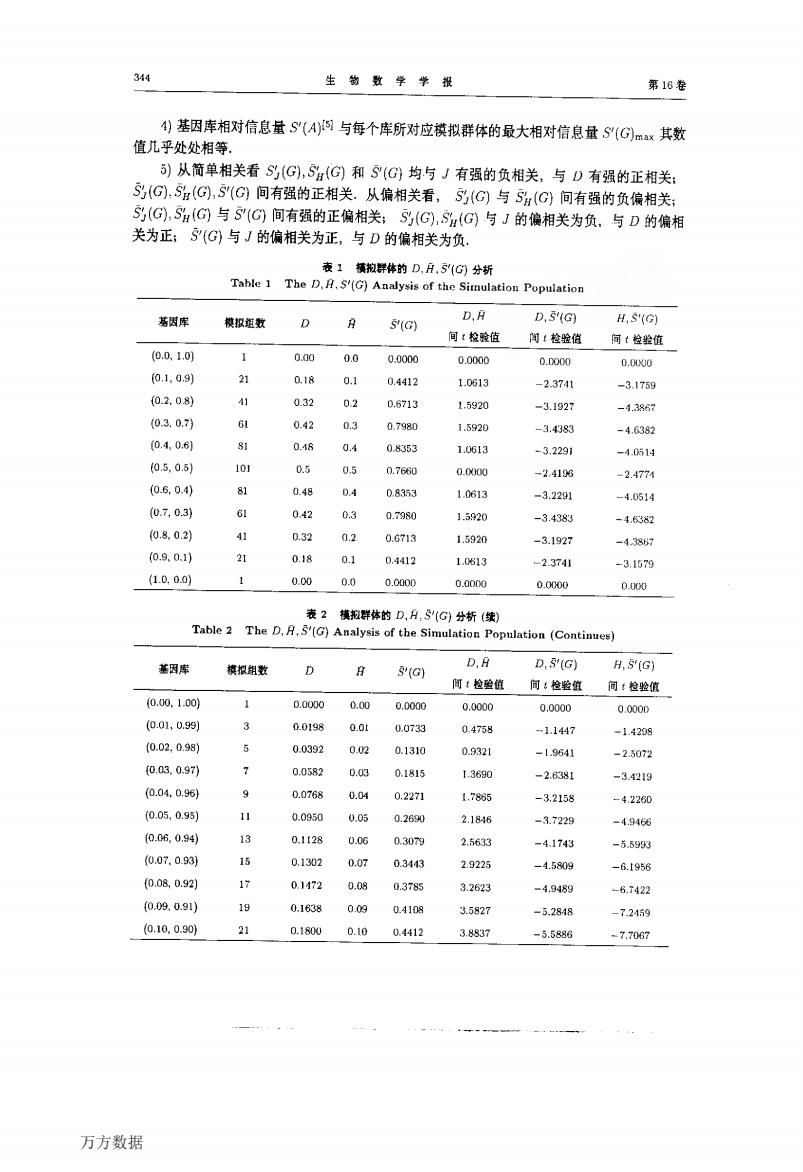
34 生箭数学学报 第16卷 4)基因库相对信息量S(A)网与每个库所对应模拟群体的最大相对信息量S(G)x其数 值儿乎处处相等. )从简单相关看S(G,S(G和S(G均与J有强的负相关,与D有强的正相关: 5(G).5(©,S"(G间有强的正相关.从偏相关看 S到1G与Sn(G,间有强的负偏相关: S(G,S(G与S(G间有强的正偏相关5乃1G,S4(G)与J的偏相关为负,与D的偏相 关为正: S(G)与J的偏相关为正,与D的偏相关为负. 横拘群体的D,户,5C分桥 S'(G)Analysis of the Simulation Population 葛因库 D S(G) D,S'(G) H,S(的 可‘检酸值 闻4粒验值 简:检验值 0.00 0.0 0.0000 0.0000 0.0m00 0.00 01,09) 21 0.18 0.1 0.4412 10%13 -2.374 -31759 0.2.081 0.32 02 06713 15920 -3192 -1386 03.0.7 0.42 0.798 1.5920 -3.4083 -4.6381 0405 0. 0.4 0.8353 1.0613 -3.2291 -40514 (05,05 10 0.5 0.76 -4108 -24774 06.0.4) 8】 0.4 1613 -322 -1051 0.7.0.31 3 0 1.592 -34383 -48382 0802 0.32 0.G713 1.5020 -3.1927 -d3867 (09.0.1 21 0.18 0.4412 1.0513 -23741 -3159 (1.0.0.0) 0.00 0.0 0.00 0.000 D.0C0 cion (Continues) 因库 横和组数 0 D,S'(G) H,'(G 间:检验 间:检验值 .0.1.0间 0.000 0.o 0.000 0.0000 0,0000 0.0000 0.01,0.9 0.0198 0.0t 00735 0.458 -1144 -1.4238 0.02,098 0.0392 0.02 0.1310 0.932 -19641 2.5072 0.03.0.97 0.0582 o. 13690 -26 0.04.096 -3.4219 0.076 0.01 0,2271 1.786 -3.2138 -4.2250 0.05,095 0.0050 0.05 0.2690 2.184 -372 -49465 0.06.094 0.1128 0.06 0.307 2563 -41743 5g (0.07.0.93 0.1302 2022 -1580 -6.195 0.147 0.09 0.378 3.262 -4.8489 -67422 (0.09.0.91 19 0.1638 003 0.4108 3.582 -32848 -7.24150 0.10,0.90j 21 0.180U 0.10 Q412 337 -5.5886 -7.700 万方数据
万方数据
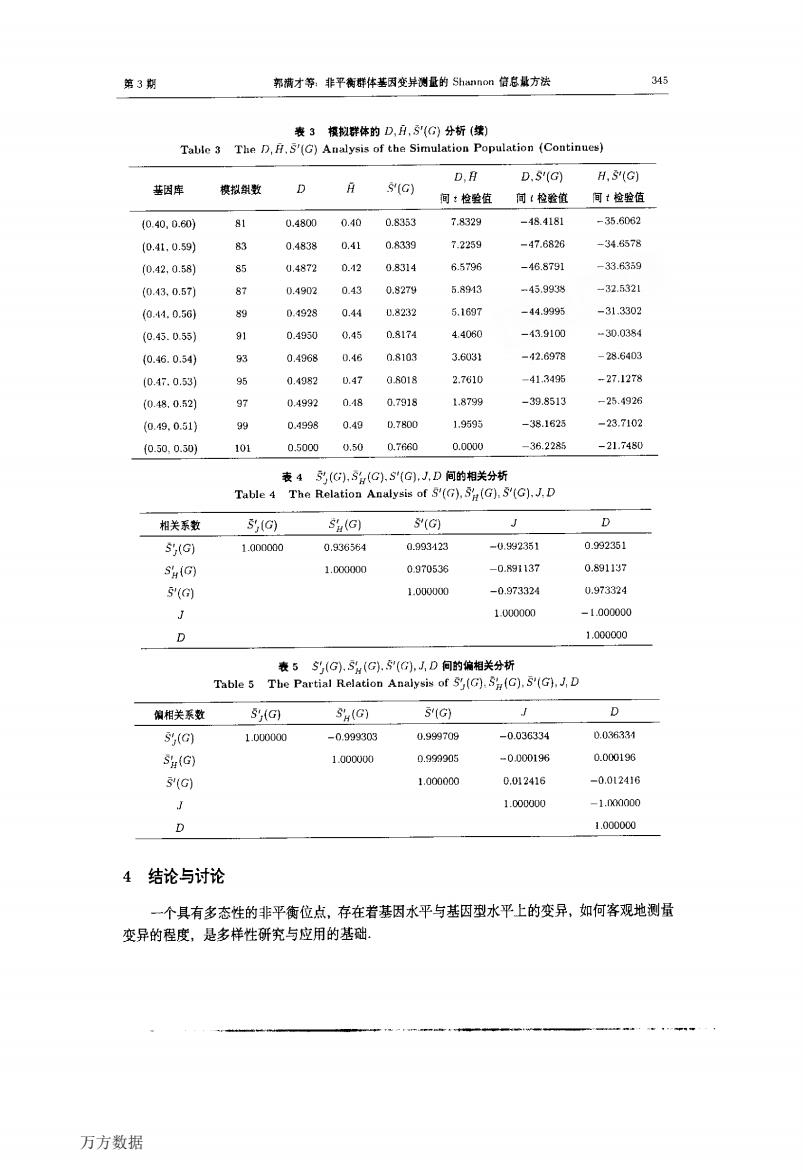
剪3期 郭满才等非平衡群体基因变量的Shannon倍方法 制体的D..G1分析 D.B D.S'(G) H,(G) 模拟织数 D G 间:检验值间:松验值阁1检验值 (0.40,0.60) a.4800 00 08353 78329 356032 (0.41.0.59) 83 04838 0.41 0.8339 72258 -47682到 -34657 0.42,0.58) 85 04872 012 0&314 6.5796 .465791 -33.8359 (043.0.5) 87 04902 0.827y 593 45.993 -32.532 (0.44.0.30 028 -49 -313302 (0.43.0.55) 91 0.4950 0.45 0.817 4.06 -43.9100 -30098 0.46.05 0.4968 046 nR103 3.6031 -42.6978 286403 04.03) 0018 2.7610 413195 27.1278 (0.48.0.52】 97 0493 1879 -39513 25.926 (049.0.51) 99 0.4508 0.40 D.7800 1.959 -38.1625 -237102 10.50.0.50 101 0.5000 0.500.70 0.0000 -36.2285 -21.7450 表4S,,S(G)S(G.,D间的相关分析 Table 4 The Relation Analysis of S().(G).S(C).J.D 相关系数 5(G) S(G) S(G) J 0 1.000000 0.936554 0903123 -0.8g2351 0.992351 S(G) 1.000m 0970536 -0.9137 0.591137 5() 1.0000 -0.97324 0.97332 1.000000 -1.00000 1.000000 表5S(G.S4(G.(G.1D间的偏相关分桥 Table5 The Partial Relation Analysisof)(C).)D 粮相关系数 Sy(G) Su(G) 5G分 D 100000 -0.999303 0.999709 -0036334 0036334 S(G 1.000w -0000196 0.000196 5(G 1.000000 0.02416 -001241 1.00000 -1.0000 1.000000 4结论与讨论 一个具有多态性的非平衡位点,存在着基因水平与基因型水平上的变异,如何客观地测量 变异的程度,是多样性研究与应用的基础. 万方数据
第3期 孛|I满才等非平衡群体基因变异测量的Shannon信息量方法 表3模拟群体的D,曰,亏’(G)分析(续 Table 3 The D,冉、S’(G)Analysis of the Simulation Population{Continues) 表5 sj(G)、雪0(G).童‘(G),正D问的偏相关分析 Table 5 Tile Partial Relation Analysis of sj(G).s;(G),S J(G),J,D 4结论与讨论 一个具有多态性的非平衡位点,存在着基因水平与基因型水平上的变异,如何客观地测量 变异的程度,是多样性研究与应用的基础. 万方数据