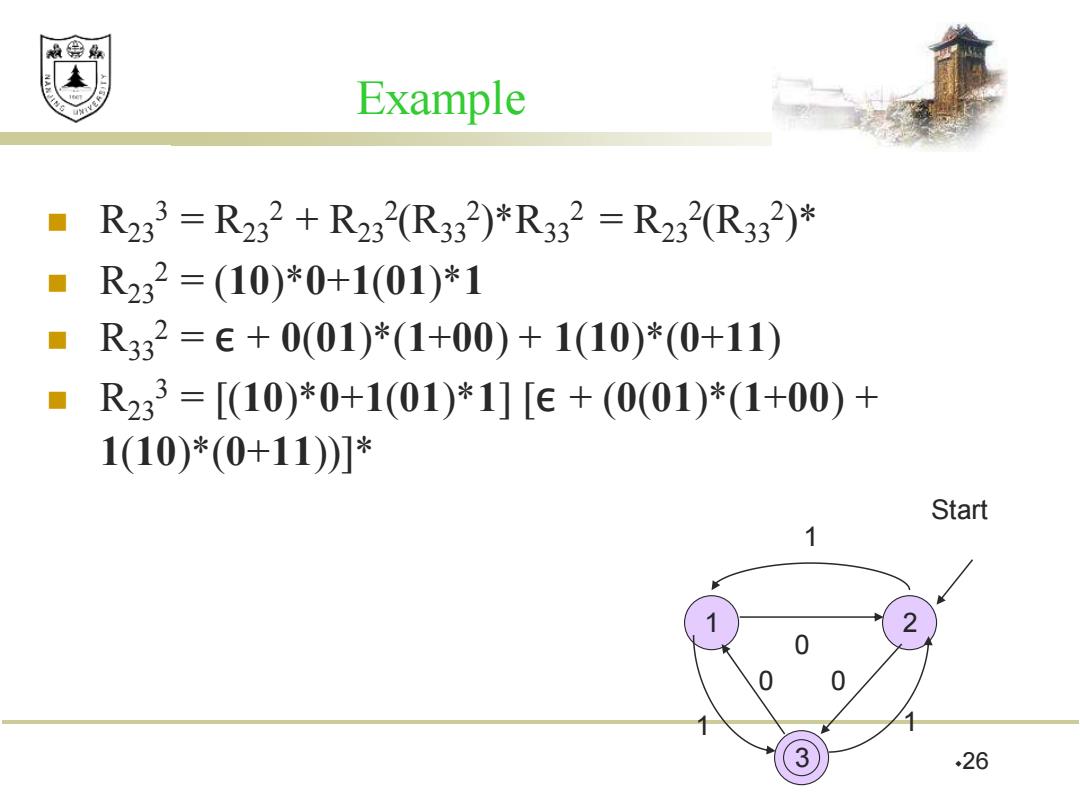
效绵鼎 Example R233=R232+R232(R332)*R332=R232(R32)* R232=(10)*0+1(01)*1 R332=€+0(01)*(1+00)+1(10)*(0+11) ■ R233=[(10)*0+1(01)*1][E+(0(01)*(1+00)+ 1(10)*(0+11)]* Start 1 1 2 0 0 3 …26
26 Example ◼ R23 3 = R23 2 + R23 2 (R33 2 )*R33 2 = R23 2 (R33 2 )* ◼ R23 2 = (10)*0+1(01)*1 ◼ R33 2 = ε + 0(01)*(1+00) + 1(10)*(0+11) ◼ R23 3 = [(10)*0+1(01)*1] [ε + (0(01)*(1+00) + 1(10)*(0+11))]* 1 3 2 0 0 0 1 1 1 Start

“绵鼎 Summary Each of the three types of automata(DFA,NFA,E- NFA)we discussed,and regular expressions as well, define exactly the same set of languages:the regular languages. 27
27 Summary ◼ Each of the three types of automata (DFA, NFA, ε- NFA) we discussed, and regular expressions as well, define exactly the same set of languages: the regular languages

效绵县 Algebraic Laws for RE's Union and concatenation behave sort of like addition and multiplication. o is commutative and associative:concatenation is associative. Concatenation distributes over + o Exception:Concatenation is not commutative. 28
28 Algebraic Laws for RE’s ◼ Union and concatenation behave sort of like addition and multiplication. + is commutative and associative; concatenation is associative. Concatenation distributes over +. Exception: Concatenation is not commutative

效绵鼎 Identities and Annihilators ☑is the identity for+. oR+☑=R e is the identity for concatenation. O ER=RE=R. is the annihilator for concatenation. o☑R=R☑=☑ 29
29 Identities and Annihilators ◼ ∅ is the identity for +. R + ∅ = R. ◼ ε is the identity for concatenation. εR = Rε = R. ◼ ∅ is the annihilator for concatenation. ∅R = R∅ = ∅

NANJING UNIVERSITY Decision Properties of Regular Languages General Discussion of “Properties” The Pumping Lemma Membership,Emptiness,Etc. .30
30 Decision Properties of Regular Languages General Discussion of “Properties” The Pumping Lemma Membership, Emptiness, Etc