
效绵鼎 k-Path induction Let Rik be the regular expression for the set of labels of k-paths from state i to state j. Basis:k=0.Ri=sum of labels of arc from i to j. 0 ☑if no such arc. 0 But add e if i=j 21
21 k-Path Induction ◼ Let Rij k be the regular expression for the set of labels of k-paths from state i to state j. ◼ Basis: k=0. Rij 0 = sum of labels of arc from i to j. ∅ if no such arc. But add ε if i=j
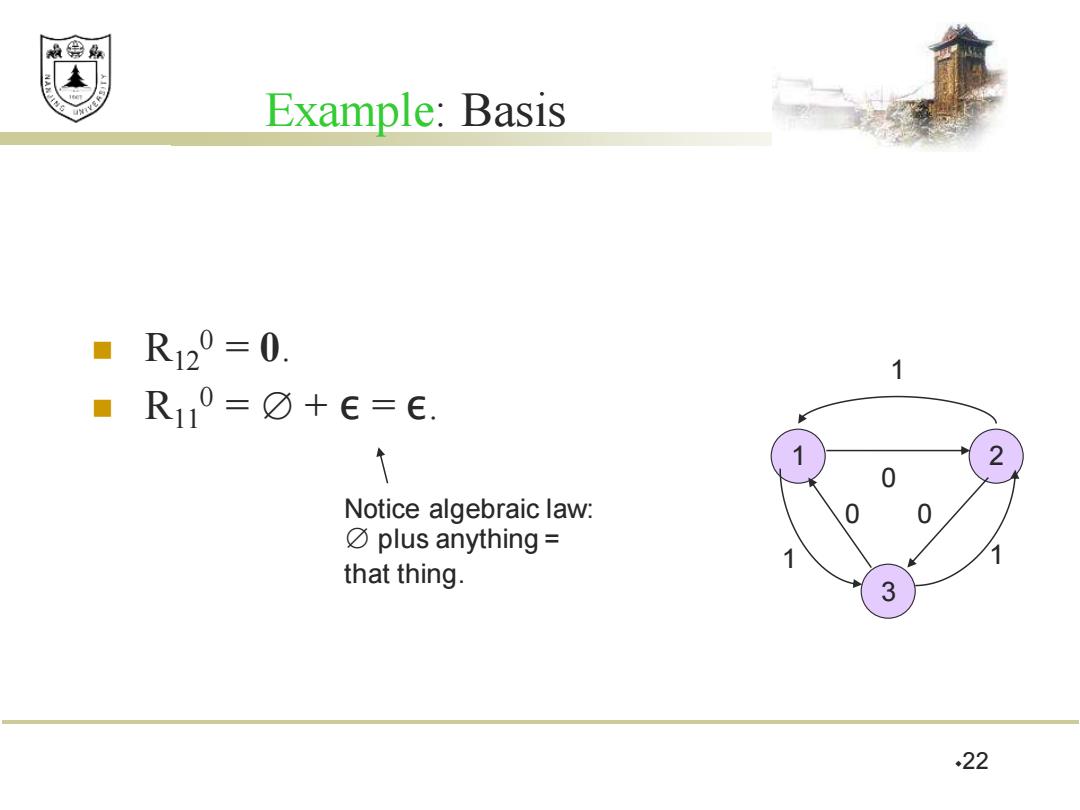
效绵鼎 Example:Basis R12°=0. 1 R10=0+E=E. ↑ 2 0 Notice algebraic law: 0 ☑plus anything= that thing. 1 3 22
22 Example: Basis ◼ R12 0 = 0. ◼ R11 0 = ∅ + ε = ε. 1 3 2 0 0 0 1 1 1 Notice algebraic law: ∅ plus anything = that thing

效绵鼎 k-Path Inductive Case A k-path from i to j either: 1. Never goes through state k,or 2. Goes through k one or more times. Rik=RijkI+Rikk-(Rkkk-1)*Rkjk-1 Goes from i to k the Then,from Doesn't go first time k to j through k Zero or more times from k to k .23
23 k-Path Inductive Case ◼ A k-path from i to j either: 1. Never goes through state k, or 2. Goes through k one or more times. Rij k = Rij k-1 + Rik k-1 (Rkk k-1 )* Rkj k-1 . Doesn’t go through k Goes from i to k the first time Zero or more times from k to k Then, from k to j
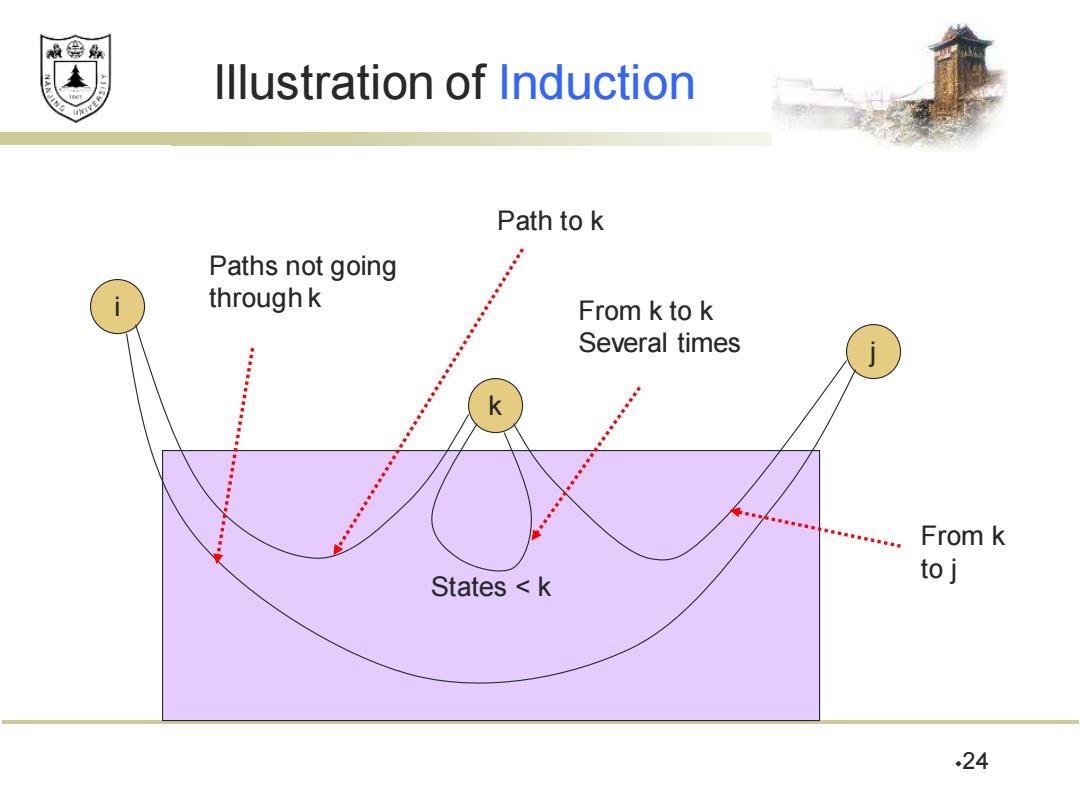
效绵鼎 Illustration of Induction Path to k Paths not going i through k From k to k Several times k From k to j States k 24
24 Illustration of Induction States < k k i j Paths not going through k From k to j From k to k Several times Path to k

效绵鼎 Final Step The RE with the same language as the DFA is the sum (union)of Ri",where: 1. n is the number of states;i.e.,paths are unconstrained. 2.i is the start state. 3.j is one of the final states. .25
25 Final Step ◼ The RE with the same language as the DFA is the sum (union) of Rij n , where: 1. n is the number of states; i.e., paths are unconstrained. 2. i is the start state. 3. j is one of the final states