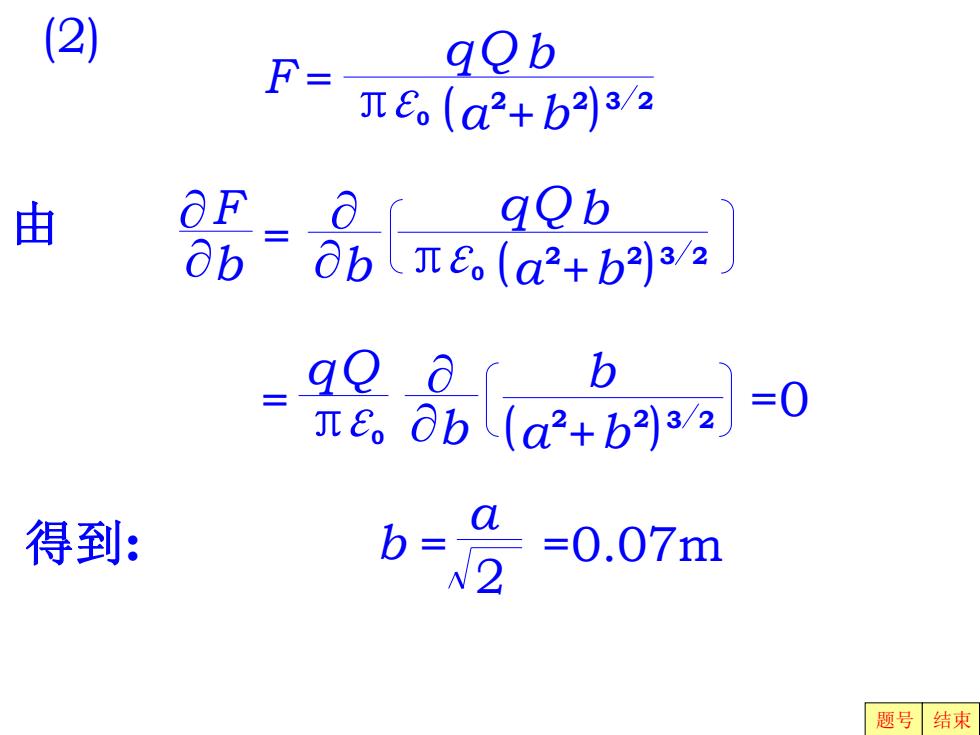
(2) F= qob Le。(a2+b2)3/2 由 oF= qOb O 0bLe(a2+b2)32 品a46pa-0 ao a 得到: b22 =0.07m 题号结束
π q ε0 Q ( ) b 2 a + 2 b = 3 2 b =0 b a = 2 得到: =0.07m π q ε0 Q ( ) = b 2 a + 2 b 3 2 F (2) F b π q ε0 Q ( ) b 2 a + 2 b = 3 2 b 由 题号 结束

8-3在边长为2cm的等边三角形的顶点 上,分别放置电荷量为91=1.0×106C、 92=3.0×10-6C、和q3=-1.0×10-6C、的点 电荷。 (1)哪一个点电荷 所受的力最大? (2)求作用在q2上 力的大小和方向。 3 02 题号结束
8-3 在边长为2cm的等边三角形的顶点 上,分别放置电荷量为q1=1.0×10-6C、 q2=3.0×10-6C、和q3 =-1.0×10-6C、的点 电荷。 (1)哪一个点电荷 所受的力最大? (2)求作用在q2上 力的大小和方向。 题号 结束 q 2 q 1 q 3

己知:a=2cm, q1=1.0×10-6C, 92=3×10-6C,q3=-1.0×106C, 求:(1)F,F2,F3, 9=1×106 (2)F2 解:(1)q1,92,9s 9公=3×10-6 受力方向如图 9s=-1×1060yT F2 q192 F=Fa=4nBoa ,1×3×1012 =9×109×4×104 =67.5N 题号结束
q1=1×10-6 q3 =-1×10-6 q2=3×10-6 a q . . . F2 F3 F1 已知: a = 2cm, q1 =1.0×10-6 C, q2 =3×10-6 C, q3 = -1.0×10-6 C, 求: (1) F1 , F2 , F3 , 解: (1) q1 , q2 , q3 π a 4ε 2 0 F12 = F21 = q1 q2 = 9×109× =67.5N 1×3×10-12 4×10-4 题号 结束 受力方向如图 (2) F2
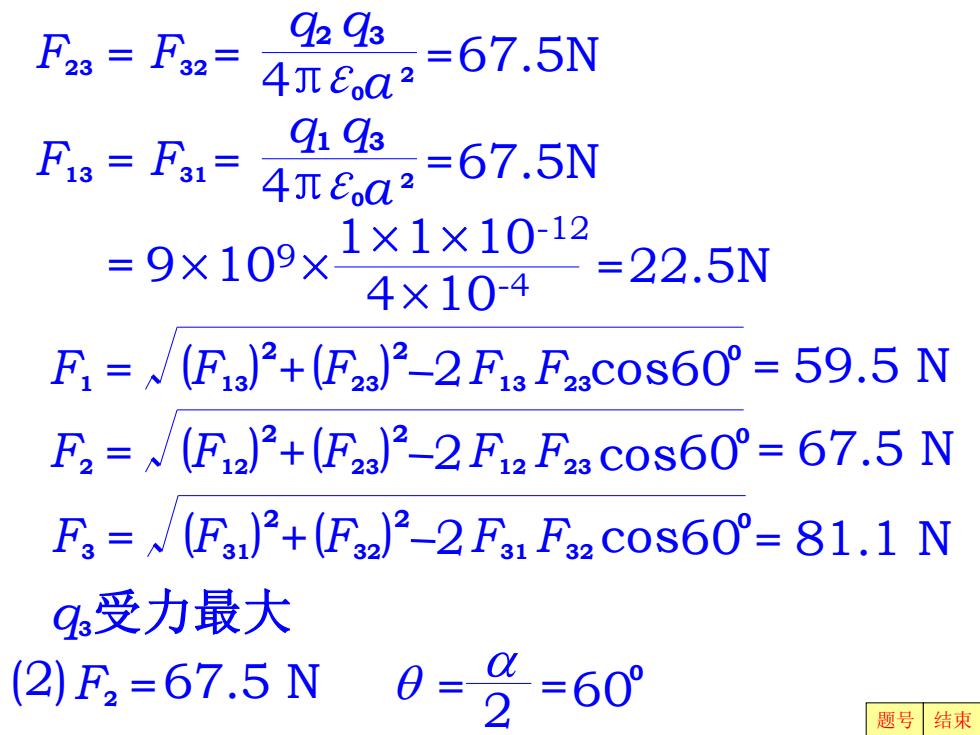
F23=F32= 9293 4T8a2 =67.5N 9193 F3=F31=4元ea2 =67.5N 9x109x1义1×10 4×10-4 =22.5N F=J(Fg)2+(F232-2F3Fc0s60°=59.5N F2=(F22+(F2)2-2F12F23c0s60°=67.5N F3=J(F)2+(F2-2F1F2Cos60°=81.1N q受力最大 2)F2=67.5N 0= =60° 2 题号结束
π a 4ε 2 0 F23 = F32 = q2 q3 =67.5N π a 4ε 2 0 F13 = F31 = q1 q3 =67.5N = 9×109× =22.5N 1×1×10-12 4×10-4 2 60 59.5 N 2 0 F1 = (F13) + F13 F23 = 2 (F ) 23 cos q3受力最大 (2)F2 =67.5 N 2 60 81.1 N 2 0 F3 = (F31) + F31 F32 = 2 (F ) 32 cos 2 60 67.5 N 2 0 F2 = (F12) + F12 F23 = 2 (F ) 23 cos a q = = 2 600 题号 结束

8-4在正方形的两个相对的角上各放置 一点电荷Q,在其他两个相对角上各置一点 电荷q。如果作用在Q上的力为零。求Q与 q的关系。 题号结束
8-4 在正方形的两个相对的角上各放置 一点电荷Q,在其他两个相对角上各置一点 电荷q 。如果作用在Q上的力为零。求Q与 q 的关系。 题号 结束