
4.2.3 Types of errors P the probability of deciding D when hypothesis H is correct. p(yIHo) p(ylH) RO -b b y Figure 4.1.Probability density functions for Example 2.1 UESTC 16
16 UESTC 4.2.3 Types of errors Pij: the probability of deciding Di when hypothesis Hj is correct. R0 R1

4.2.3 Types of errors P the probability of deciding D when hypothesis His correct. Py=p(yI)dy (4.33) Po,is called the probability of a“miss”Pm Pis called the probability of detection P P10 is called the probability of false alarm P PE=兀P+π,P (4.34) UESTC 17
17 UESTC 4.2.3 Types of errors ( | ) (4.33) i ij j R P p y H dy = 0 10 1 01 (4.34) P P P E = + Pij: the probability of deciding Di when hypothesis Hj is correct. is called the probability of a “miss” P01 Pm P11 is called the probability of detection Pd P10 is called the probability of false alarm Pf

Example 4.3 In example 4.1,if we define a log-likelihood threshold as 'then -e-w P2amgw (4.35) UESTC 18
18 UESTC Example 4.3 2 ` 00 2 2 2 ` 01 2 2 2 10 2 ` 2 2 11 2 ` 2 1 ( ) exp( ) 2 2 1 ( ) exp( ) 2 2 1 ( ) exp( ) 2 2 1 ( ) exp( ) (4.35) 2 2 y b P dy y b P dy y b P dy y b P dy − − + = − − = − + = − − = − In example 4.1, if we define a log-likelihood threshold as , then
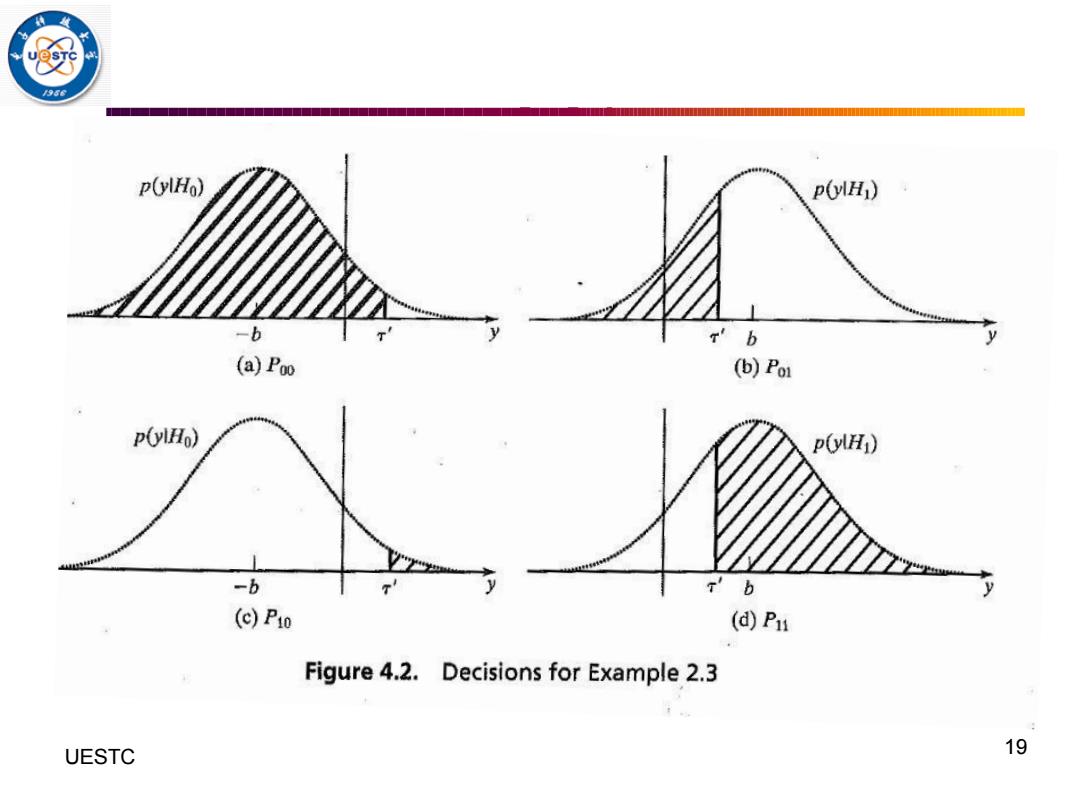
936 p(ylHo) p(ylH) -b 入 b (a)Poo (b)Pol p(ylHo) p(ylH) -b T'b (c)P0 (d)Pu Figure 4.2.Decisions for Example 2.3 UESTC 19
19 UESTC

The error function is defined as weea (4.36) and complementary error function is defined as ofe) (4.37) UESTC 20
20 UESTC 2 0 2 ( ) (4.36) z t erf z e dt − = The error function is defined as 2 2 ( ) 1 ( ) (4.37) t z erfc z e dt erf z − = = − and complementary error function is defined as