
Chapter 11 Estimation of Specific Parameters UESTC 1
1 UESTC Chapter 11 Estimation of Specific Parameters

11.1 Chapter highlights Parameter estimation in WGN Amplitude estimation in the coherent case Amplitude estimation in the noncoherent case Phase estimation in WGN Time-delay estimation in WGN Frequency estimation in WGN UESTC 2
2 UESTC 11.1 Chapter highlights • Parameter estimation in WGN • Amplitude estimation in the coherent case • Amplitude estimation in the noncoherent case • Phase estimation in WGN • Time-delay estimation in WGN • Frequency estimation in WGN

11.2 Parameter estimation in WGN Assume k samples of the measured signal are y;=s;(a)+n,i=1,...,k where the noise is zero-mean,white Gaussian noise with variance o2.Therefore, 心e7齐-ej MAP.p可mx→p(ik)+小&np(a)-0 UESTC 是立(g-aa@+npa=0
11.2 Parameter estimation in WGN Assume k samples of the measured signal are where the noise is zero-mean, white Gaussian noise with variance . Therefore, MAP: 3 UESTC ( ) , 1, , i i i y n = + = s i k α 2 ( ) ( ) ( ( )) 2 / 2 2 2 1 1 1 exp 2 2 k k i i i p y y s = = − − ln ln 0 p y p ( ) ( ) + = p y ( ) max ( ( )) ( ) ( ) 2 1 1 ln 0 k i i i i s y s p = − + =
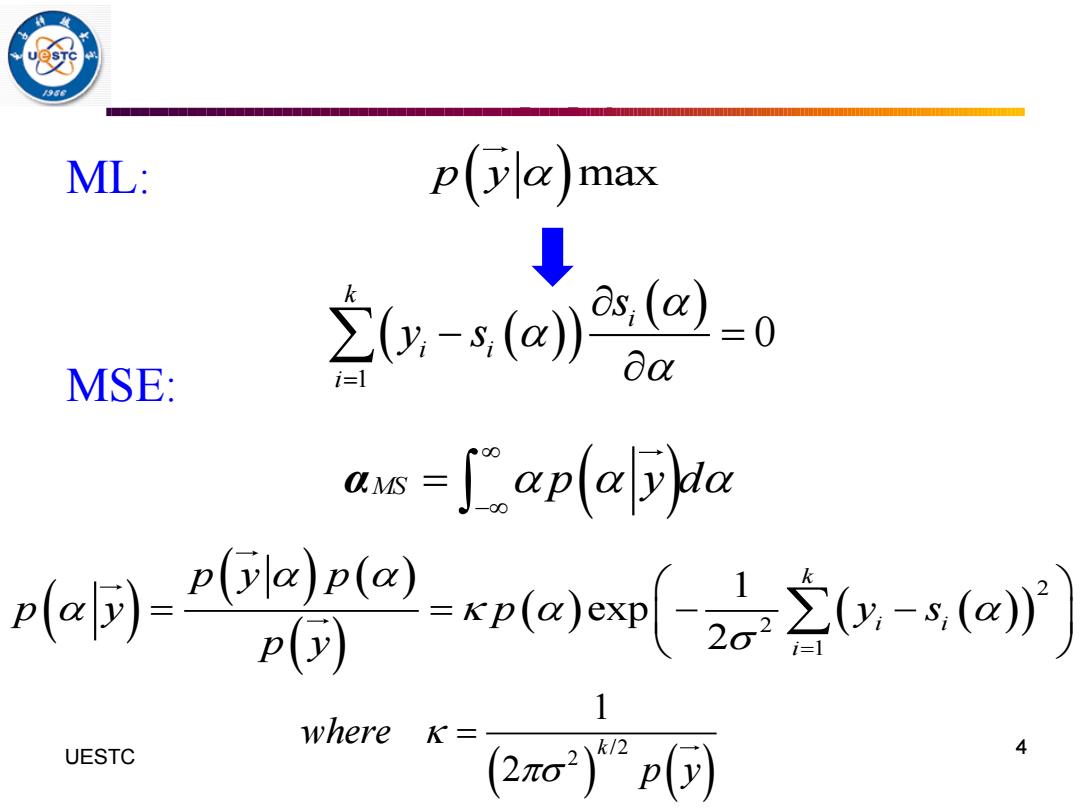
ML: p(a max 20x-sj)22-0 MSE: na as-aplaya e同-4 d 1 where K= UESTC 2o2p可 4
ML: MSE: 4 UESTC p y( )max ( ( )) ( ) 1 0 k i i i i s y s = − = MS p y d ( ) − = α ( ) ( ) ( ) ( ) ( ) ( ( ))2 2 1 1 exp 2 k i i i p y p p y p y s p y = = = − − ( ) ( ) / 2 2 1 2 where k p y =

5 For a ML estimate that is unbiased,the CRB provides the minimum variance that can be got. npa)-n2ar-2a立(ysai i1 品mp啡a之yag I- ↓ 品5网-空控n@- UESTC
For a ML estimate that is unbiased, the CRB provides the minimum variance that can be got. 5 UESTC ( ) ( ( )) 2 2 2 1 1 ln ln 2 2 2 k i i i k p y y s = = − − − ( ) ( ( )) ( ) 2 1 1 ln k i i i i s p y y s = = − ( ) ( ) ( ) ( ) 2 2 4 2 1 1 1 1 1 ln k k k i i j i j i j i s s s E p y E = = = = = n n