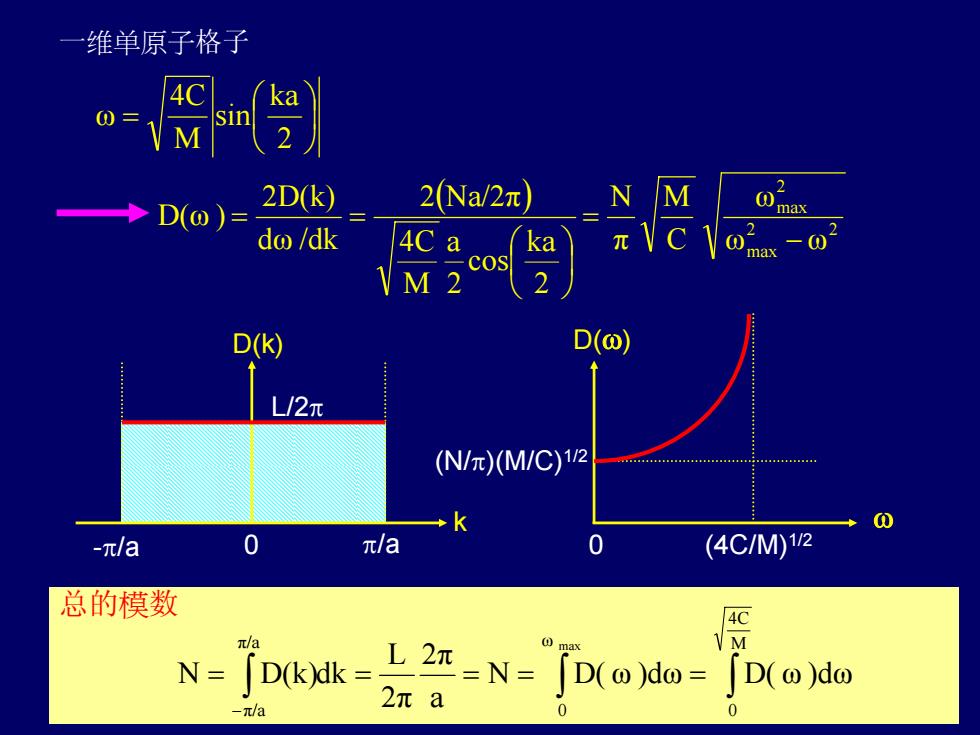
一维单原子格子 ka \M 2 2Na/2元 N M D(o)= 2D(k) max do /dk 4C a a 02 D(k) D(@) LU/2元 (N/m)M/C)12 -π/a 0 π/a 0 (4C/M12 总的模数 VM N=D(kXk=12z-N=[D(o)do=D(o)do π/a max -π/a 2πa 0 0
6 一维单原子格子 ( ) 2 2 max 2 max ωω ω C M π N 2 ka cos 2 a M 4C 2 Na/2π ω /dkd 2D(k) ω ) D( 2 ka sin M 4C ω − = ⎟⎠⎞ ⎜⎝⎛ == ⎟⎠⎞ ⎜⎝⎛ = D(ω) k ω D(k) L/2π -π/a 0 π/a (N/π)(M/C)1/2 (4C/M)1/2 0 总的模数 D(N ω ω D()d ω ω )d a 2π 2π L dkD(k)N M 4C 0 ω 0 π/a π/a max ∫ ∫∫ = === = −

二维情况: 周期性边界条件,在边长为L的正方形中有NP个原胞 exp[i(kx+k y)]exp[i(kx(x+L)+k(y+L)) 当Kx,K,=0,± 4π6元 工一L,-L 在k-空间中单位面积的模数 在k-空间里波矢从k到k+dk的模数 L D(k)dk= △k△k dk,dky= 2πkdk 4π 单位频率区域的模数 D(O)= D(k) A2元k1 do/dk 4 D(k)V 三维情况: D(0)= 4k21 do/dk 8n3
7 二维情况 : 周期性边界条件, 在边长为L 的正方形中有N2个原胞 exp[ i(kxx+kyy) ] = exp[ i( kx(x+L) + ky(y+L) ) ] 当 kx, ky = . , L6π , L4π , L2π ,0 ±±± 在k-空间中单位面积的模数 2 2 2 yx 4π L L 2π Δk Δk 1 ⎟ = ⎠⎞ ⎜⎝⎛ = − 在k-空间 里波矢从k 到 k+dk的模数 π dkk 2 4π L dkdk Δk Δk 1 D(k)dk 22 yx yx = = 单位频率区域的模数 g 2 v 1 π k 2 4π A ω /dkd D(k) D( ω ) == g 2 3 v 1 π k 4 8π V ω /dkd D(k) 三维情况 : D( ω ) ==
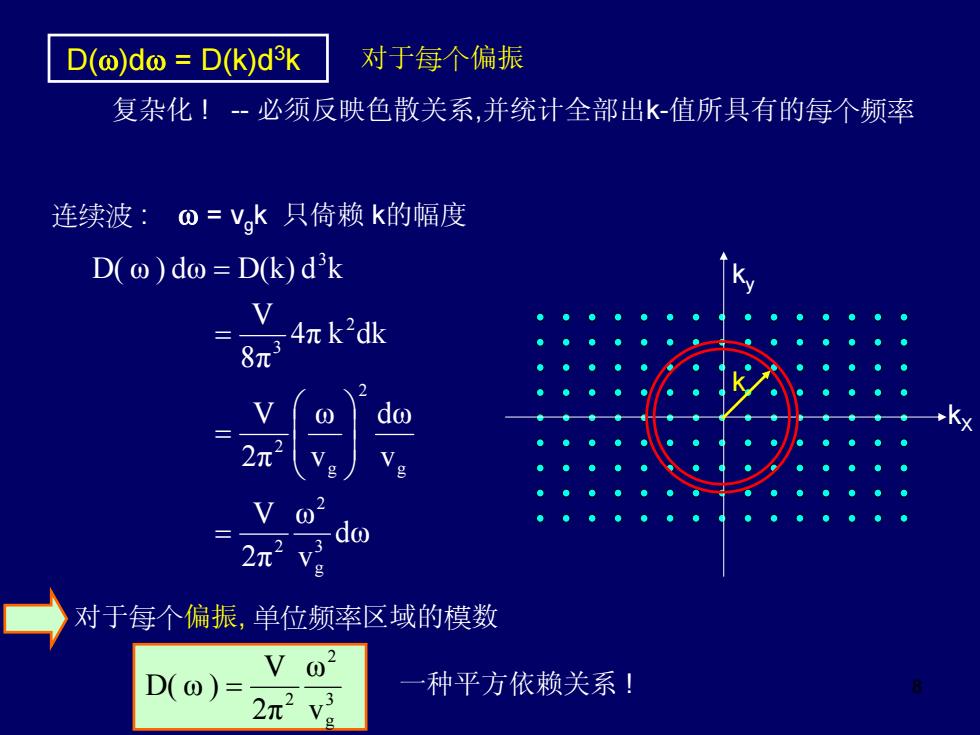
D(@)do=D(k)d3k 对于每个偏振 复杂化!-必须反映色散关系,并统计全部出k-值所具有的每个频率 连续波:O=V。k只倚赖k的幅度 D(@)do=D(k)dk 4元k2dk 8π V do 2r2 V do 3 对于每个偏振,单位频率区域的模数 V @2 D()= 2π2v 种平方依赖关系!
8 D(ω)dω = D(k)d3k 复杂化 ! - 必须反映色散关系,并统计全部出k-值所具有的每个频率 连续波 : ω = vgk 只倚赖 k的幅度 dω v ω 2π V v dω v ω 2π V π dkk 4 8π V D( ω ) ω kd D(k)d 3 g 2 2 g 2 g 2 2 3 3 = ⎟⎟⎠⎞ ⎜⎜⎝⎛ = = = 3 g 2 2 v ω 2π V D( ω ) = 对于每个偏振, 单位频率区域的模数 kX ky k 一种平方依赖关系 ! 对于每个偏振
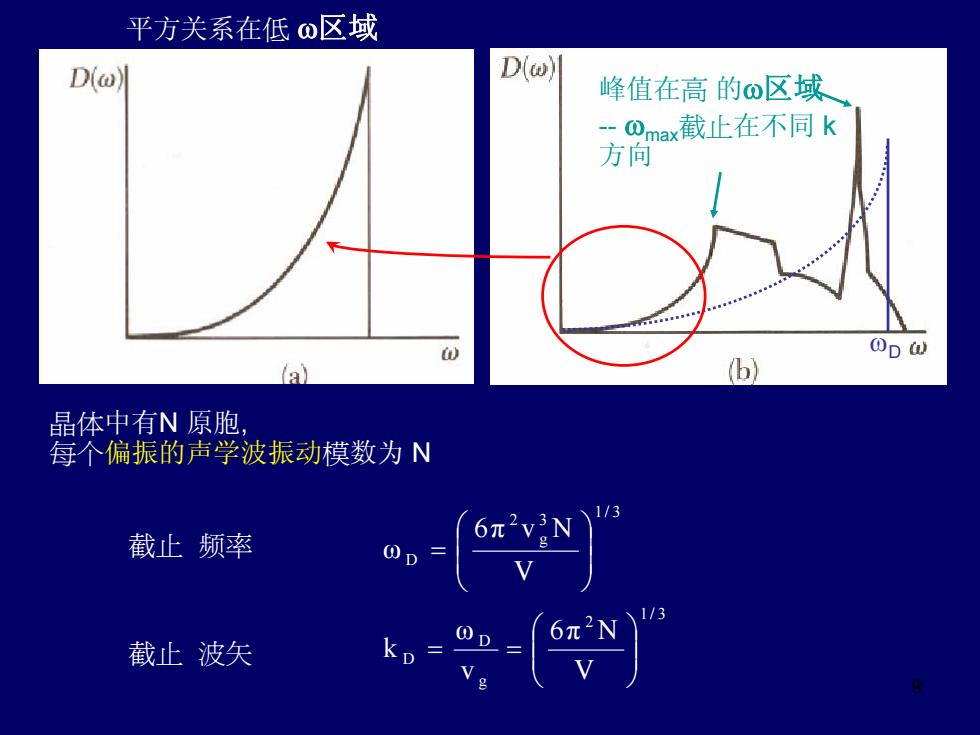
平方关系在低o区域 D(o) D(@ 峰值在高的o区域 Omax截止在不同k 方间 0D@ a】 (b) 晶体中有N原胞 每个偏振的声学波振动模数为N 截止频率 6π2N 截止波矢
9 平方关系在低 ω区域 ωD 峰值在高 的ω区域 - ωmax截止在不同 k 方向 晶体中有N 原胞, 每个偏振的声学波振动模数为 N 3/1 2 g D D 3/1 3 g 2 D V π N6 v ω k V π Nv6 ω ⎟⎟⎠⎞ ⎜⎜⎝⎛ == ⎟⎟⎠⎞ ⎜⎜⎝⎛ 截止 频率 = 截止 波矢
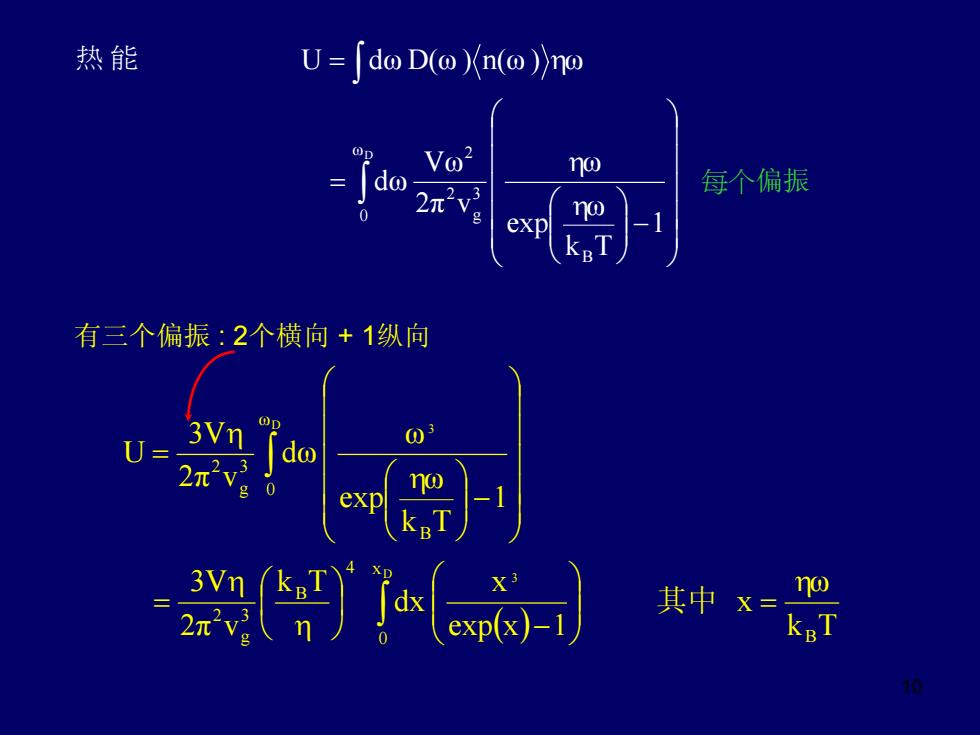
热能 U=do D(o)n())no Vo2 ro 每个偏振 no exp 有三个偏振:2个横向+1纵向 U= 3Vn @D do exp 其中x= no
10 ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ −⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = = ∫ ∫ 1 Tk ω exp ω π v2 V ω ω d U ω d ω ) D( ω ) n( ω B 3 g 2 ω 2 0 D η η 热 能 η 每个偏振 有三个偏振 : 2个横向 + 1纵向 ( ) Tk ω x 1xexp x dx Tk π v2 3V 1 Tk ω exp ω ω d π v2 3V U B x 0 4 B 3 g 2 B ω 0 3 g 2 D 3 D 3 η η η η η = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ −⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = ∫ ∫ 其中