
电容元件与电感元件的比较: 电容C 电感L 电压u 电流i 变量 电荷q 磁链W q=Cu w=Li 关系式 i=cdu di u=I dt dt Wc=Cu2= 1 1 2 Wz=,Li2=于 2 结论: ()元件方程是同一类型; (2)若把u-l,qy,C-L,u互换,可由电容元件 的方程得到电感元件的方程; (3)C和L称为对偶元件,平、等称为对偶元素。 显然,R、G也是一对对偶元素: U=RI←→=GU =UR→U=I/G
电容元件与电感元件的比较: 电容 C 电感 L 变量 电流 i 磁链 关系式 电压 u 电荷 q 结论:(1) 元件方程是同一类型; (2) 若把 u-I,q- ,C-L, i-u互换,可由电容元件 的方程得到电感元件的方程; (3) C 和 L称为对偶元件, 、q等称为对偶元素。 * 显然,R、G也是一对对偶元素: I=U/R U=I/G U=RI I=GU 2 2 2 1 2 1 d d ψ L W Li t i u L ψ Li L 2 2 2 1 2 1 d d q C W Cu t u i C q Cu C

§3.2储能元件和换路定则 WXH H 3.2.1.稳态”与 “暂态”的概念 开关K闭合 电路处于新稳态 电路处于旧稳态 暂态 稳态 过渡过程: 旧稳态→ 新稳态
WXH WXH t E C u 暂态 稳态 旧稳态 新稳态 过渡过程 : C 电路处于旧稳态 K R E + _ C u 开关K闭合 §3.2储能元件和换路定则 电路处于新稳态 R E + _ C u 3.2.1.“稳态”与 “暂态”的概念:
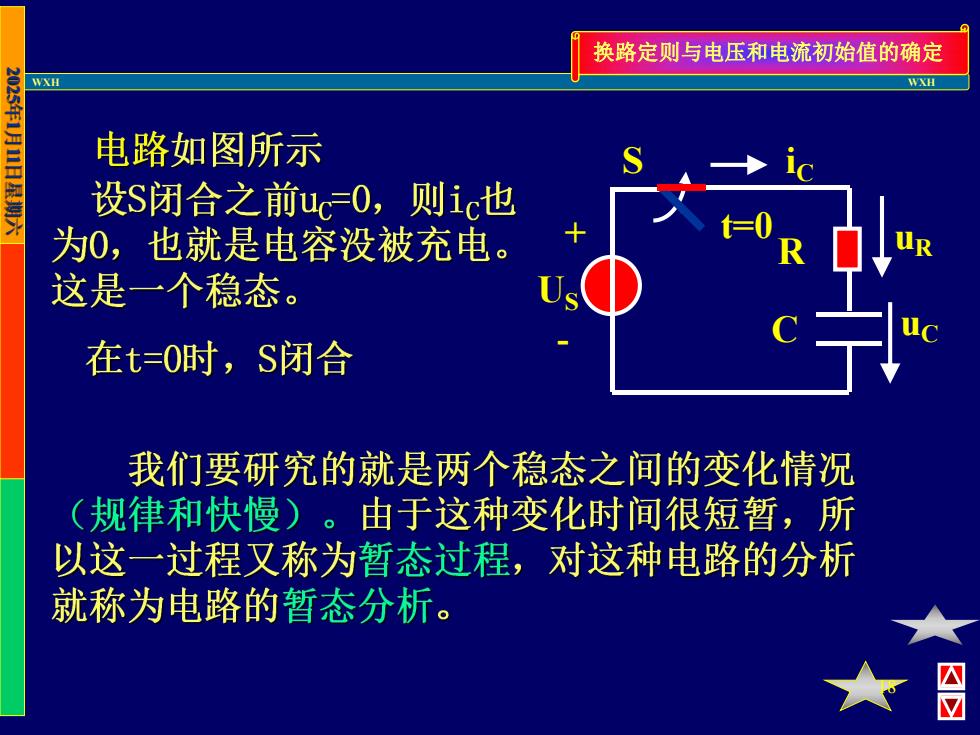
换路定则与电压和电流初始值的确定 WXH 2S 025 电路如图所示 设S闭合之前ueO,则ic也 为0,也就是电容没被充电。 这是一个稳态。 在t=0时,S闭合 我们要研究的就是两个稳态之间的变化情况 (规律和快慢)。由于这种变化时间很短暂,所 以这一过程又称为暂态过程,对这种电路的分析 就称为电路的暂态分析
WXH WXH 18 换路定则与电压和电流初始值的确定 R C + - US t=0 S uR uC iC
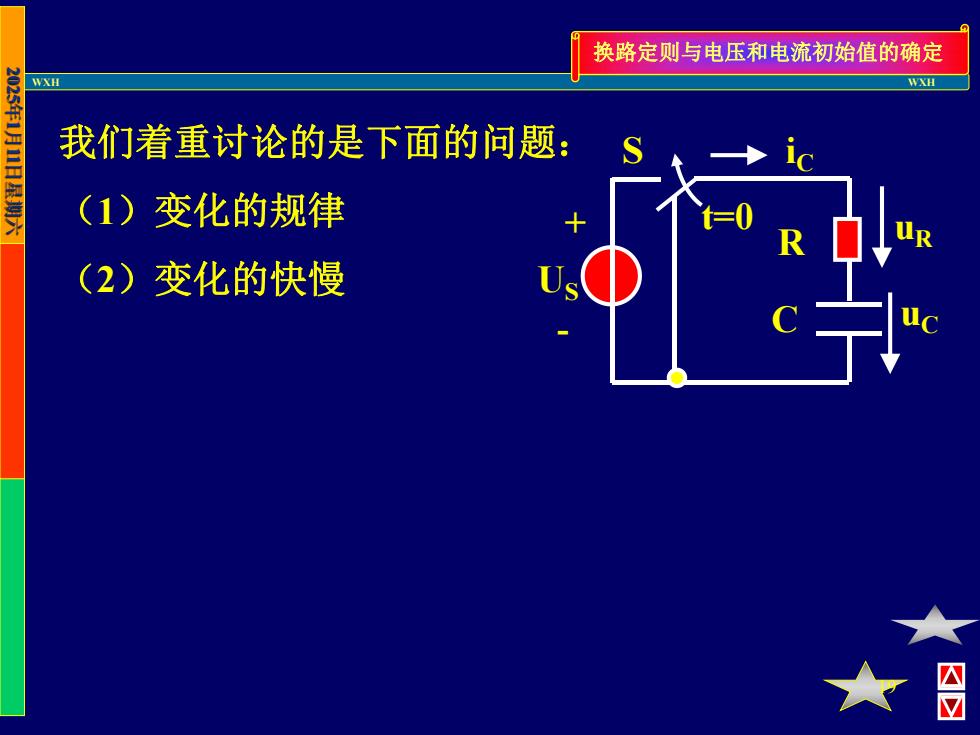
换路定则与电压和电流初始值的确定 WX WXH 我们着重讨论的是下面的问题: (1)变化的规律 (2)变化的快慢 四区
WXH WXH 19 R C + - US t=0 S uR uC 我们着重讨论的是下面的问题: iC (1)变化的规律 (2)变化的快慢 换路定则与电压和电流初始值的确定
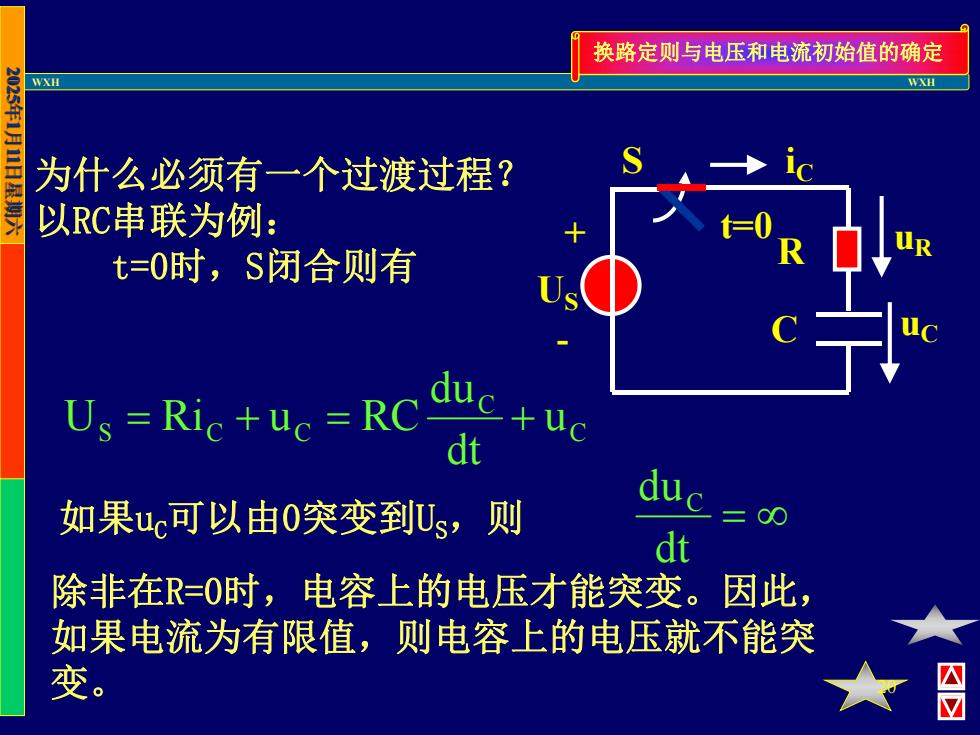
换路定则与电压和电流初始值的确定 WX 为什么必须有一个过渡过程? 以RC串联为例: t=0时,S闭合则有 Us Ric +uc RC duc+uc dt 如果u可以由0突变到Us,则 dt 除非在R=O时,电容上的电压才能突变。因此, 如果电流为有限值,则电容上的电压就不能突 变
WXH WXH 20 为什么必须有一个过渡过程? 以RC串联为例: t=0时,S闭合则有 如果uC可以由0突变到US,则 C C S C C u dt du U Ri u RC 除非在R=0时,电容上的电压才能突变。因此, 如果电流为有限值,则电容上的电压就不能突 变。 dt duC R C + - US t=0 S uR uC iC 换路定则与电压和电流初始值的确定