
E--+… E,近似地正比于是这一横向力能聚焦(而非偏转或其他)的 原因.它能提供一种指向轴的、与径向偏离成比例的横向力,偏离 越大,这个力越强,对已在轴上的粒子则完全无作用:当然,如果它 背离中轴,指向外方,就成为散焦力.容易看出,V”的大小、符号与 聚焦的关系和前文对等位面、力线的定性分析一致, 等位面V 电场Er 电场E 轴上电位 Z 电场Ez 》加速 低电位 高电位 聚焦 V>0(加速)V">0(聚焦) 《电场E 17
17 z r 电场Ez e 电场Er e 聚焦 加速 z z r 电场E 等位面V e e e 电场E 低电位 高电位 轴上电位 V'>0(加速) V">0(聚焦)

回到等位面形状.由以 上公式可得到定量关系: 之轴上取一点,如该 点处V'()与V”()皆不 等于0,则过该点的等位面 在近轴处为一旋转双曲面, 如图1.1所示.令量纲为长 度的量a= V'() 图1.1 V"(z) ,此双曲 面过而向一a方向凸 起,子午面上的截线是双曲线,其方程为 -(a-a)] 2 =1 a 2d 渐近线为过(一a,0)点的斜率为tga=士2(与轴的交角a= 士5444')的两条直线,焦点坐标之=+(3-1)a,≈=处双曲 面顶点的曲率半径为2a. 18
18
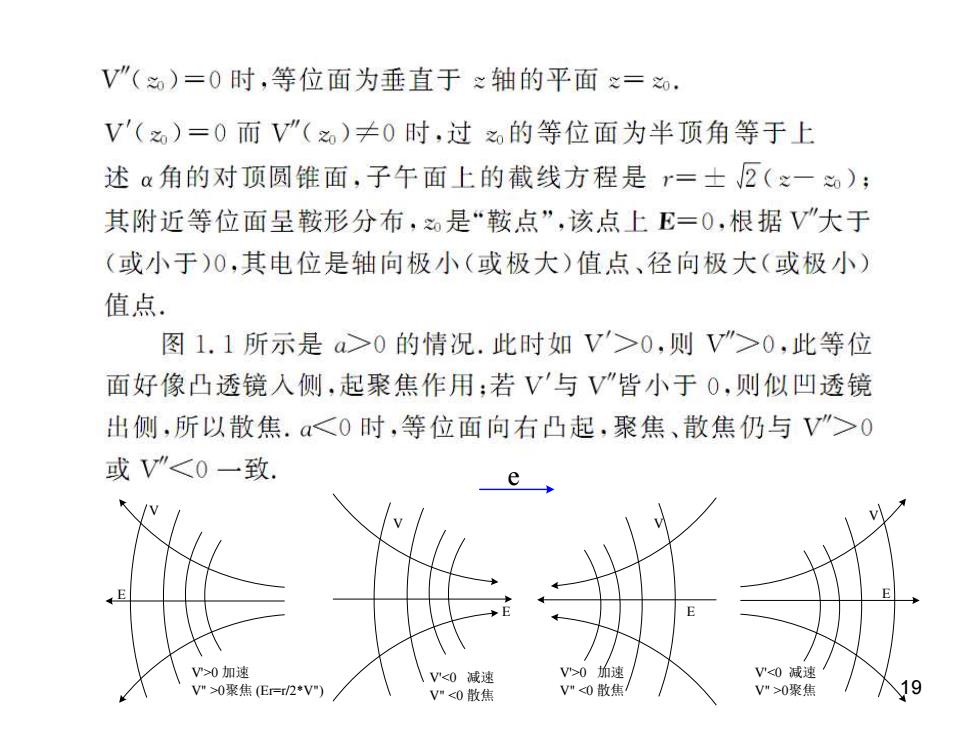
V”()=0时,等位面为垂直于之轴的平面心=. V'()=0而V”()≠0时,过的等位面为半顶角等于上 述α角的对顶圆锥面,子午面上的截线方程是r=士2(之一≈): 其附近等位面呈鞍形分布,是“鞍点”,该点上E=0,根据V"大于 (或小于)0,其电位是轴向极小(或极大)值点、径向极大(或极小) 值点. 图1.1所示是a>0的情况.此时如V'>0,则V">0,此等位 面好像凸透镜人侧,起聚焦作用:若V'与V”皆小于0,则似凹透镜 出侧,所以散焦.a<0时,等位面向右凸起,聚焦、散焦仍与V”>0 或V"<0一致. e /v V>0加速 NV<0减速 V>0折速 V"<0减速 V"0聚焦(E=/2*V) V"<0散焦 V"<0散焦 V">0聚焦 \19
19 E V e V'>0 加速 V" >0聚焦 (Er=r/2*V") E V V'<0 减速 V" >0聚焦 E V V'<0 减速 V" <0 散焦 V'>0 加速 V" <0 散焦 E V

V(,)=V()-V(xr+w(r-… 64 推导要点在点处将电位沿轴向展开,得 V)=V()+v'()(e-)+2v()(-2+… 再利用谢尔赤公式沿径向展开.两式综合,则等位面方程为 V(x,r)=V(%)+V'(%)(x-∞) +([(--r]+… =V() 只考虑(,0)点附近,可将高次项略去, V"=0或V'=0时结果易得.否则,可写成 -P+2a(x-)-7f=0 剩下的只有解析几何计算了· 该式对x微分,可得 2[x-(0-a)]-r'=0 2-r2-m"=0 代入p=1十) ,即得曲率半径. 20
20

顺便提一下,处理电子问题,有人愿意把E变号,使其大于0 时加速,方向与电子受力一致;同样,电荷、电流密度ρ和J也可以 变号,使对于电子是正的.虽本书不取,只要自己和相应计算程序 不糊涂,并无坏处.类似地,B的符号也可根据方便自行定义, 谢尔赤公式形式上规定了:轴上电位分布唯一地决定“全空 间”的电位分布.这是拉氏方程的性质,所谓全空间的场具有“牵一 发动全身”的连带关系和“求细节可以知高远”.本书未予过分强 调,因为此说法易产生误解.场的高阶微商无论计算或实测皆难以 准确获得;满足拉氏方程的“调和函数”具有调和、平均的特性一 空间中任意取一球面,该函数在球心取球面所有点的平均值,球内 函数之极大、极小值必在球面上,所以边界附近即使有较大变化, 到轴附近的反映已极细微,可能近于不可知.反过来,由中央求外 部,任何误差必被放大,可能使上述说法失去意义. 21
21