
在束流光学中,束流一般在高真空环境中,故式中介电常数€ 和磁导率可用真空中的ε。和h代替,而场向量D和H可分别 以E和B取代;不考虑空间电荷效应时,可忽略空间电荷密度P 和空间电流密度J(考虑时,勿忘电子电荷带来的负号):绝大多数 情况下,电磁场为静态或似稳态(随时间变化甚慢),故各量对t的 偏微商可取为0. V.E= 7·E=0 E0 7·B=0 7·B=0 VxE=-a1 V×E=0 ∂E V×B=0J+o0at 7×B=0 所以,本章(大多数情况下全书亦然)认为电场强度E和磁场 强度B都是散度、旋度皆为0的向量场
7

E作为无旋场,可用静电位场V描述,E=一V. B作为无源场,可用向量势场A(附加条件:A无源,即7·A =0)描述,B=7×A.当B亦无旋时,也可形式地用标量磁位Vm 描述.本书一般直接用B,而不用Vm或A,也很少用到场向量H. 因为作者以为,B能通过洛伦兹力作用于带电粒子、与场的空间储 能相联系、可以直接测量,所以唯它有资格“真实”地在物理意义上 代表磁场(一如E之于电场),“磁场强度”之名亦只有它可当之无 愧,而其他量在某种程度上只具有数学意义 既然皆是无旋无源的轴对称场,本章中E和B在近轴区域满 足同样的偏微分方程,其定性特征相似,但与边界条件的关系和生 成的方式迥然不同. 8
8
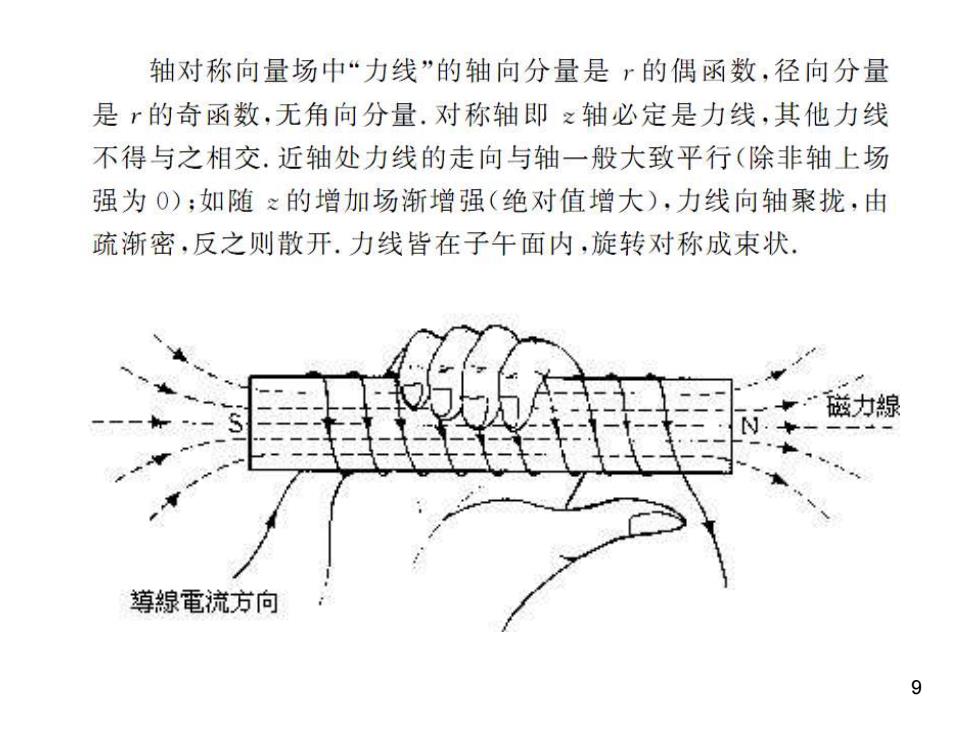
轴对称向量场中“力线”的轴向分量是r的偶函数,径向分量 是r的奇函数,无角向分量.对称轴即之轴必定是力线,其他力线 不得与之相交.近轴处力线的走向与轴一般大致平行(除非轴上场 强为O);如随~的增加场渐增强(绝对值增大),力线向轴聚拢,由 疏渐密,反之则散开.力线皆在子午面内,旋转对称成束状 磁力線 導線電流方向 9
9

轴对称场的位V也必是r的偶函数.V的分布可用等位面描 述,力线E是其法线.所有等位面皆为绕z轴的旋转曲面,其与子 午面的交线在近轴处近似为关于之轴对称的二次曲线,与之轴正 交(除非该点V取极值,故E=0,且易号),呈或凸或凹的弧形或 近于平行直线.以等差的多层等位面描述V,E强处其相聚紧密, 弱处则稀疏.与力线的特性综合,随~的增加,如E大致不变,则 等位面大体是等距平面,力线近乎平行;若E渐增强,则等位面渐 向左凹回,间距变小,力线会聚:若E渐减弱,则等位面渐向右凸 前,间距放宽,力线发散, 等位面V r等位面V 电场E e e 轴上电位 高电位 低电位 V<0(减速)V">O(聚焦) 电场正 10 类似,光学中的凸透镜,光子进入凸透镜减速并聚焦,折射率越大,聚焦越强
10 等位面V r r z 电场E 等位面V e e e 电场E 高电位 低电位 轴上电位 V'<0(减速) V">0(聚焦) 类似,光学中的凸透镜,光子进入凸透镜减速并聚焦,折射率n越大,聚焦越强
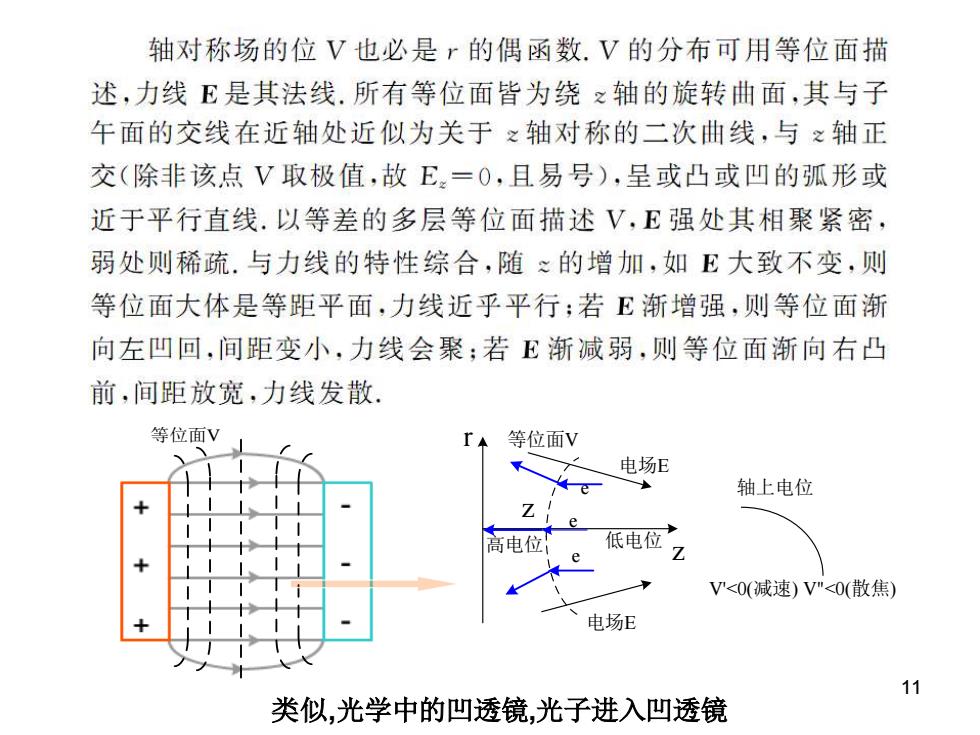
轴对称场的位V也必是r的偶函数.V的分布可用等位面描 述,力线E是其法线.所有等位面皆为绕之轴的旋转曲面,其与子 午面的交线在近轴处近似为关于之轴对称的二次曲线,与之轴正 交(除非该点V取极值,故E,=0,且易号),呈或凸或凹的弧形或 近于平行直线.以等差的多层等位面描述V,E强处其相聚紧密, 弱处则稀疏.与力线的特性综合,随≈的增加,如E大致不变,则 等位面大体是等距平面,力线近乎平行;若E渐增强,则等位面渐 向左凹回,间距变小,力线会聚;若E渐减弱,则等位面渐向右凸 前,间距放宽,力线发散 等位面V r等位面V 电场E e 轴上电位 Z e 高电位 低电位 Z V<0(减速)V"<O(散焦) 电场E 11 类似,光学中的凹透镜,光子进入凹透镜
11 等 位 面 V 类似 ,光学中的凹透镜 ,光子进入凹透镜 z z r 电 场 E 等 位 面 V e ee 电 场 E 高 电 位 低 电 位 轴 上 电 位 V ' < 0 ( 减 速 ) V " < 0 ( 散 焦 )