
第五章风险与不确定性分析 §1盈亏平衡分析 一、 线性盈亏平衡分析 令B=0,解出的0即为BEP(O) BFP (Q)-FY 进而解出生产能力利用率的盈亏平衡点BEP(): BEP(①=BEP(O)/QX100% 经营安全率: BEP(S)=1-BEP(f) 注意:平衡点的生产能力利用率一般不应大于75%经营安全率一般不 应小于25%
§1 盈亏平衡分析 一、线性盈亏平衡分析 令B=0,解出的Q即为BEP(Q) 进而解出生产能力利用率的盈亏平衡点BEP(f): BEP(f)=BEP(Q)/ Q0×100% 经营安全率: BEP(S)=1-BEP(f) 注意:平衡点的生产能力利用率一般不应大于75%;经营安全率一般不 应小于25%。 P V t F BEP Q - - ( ) = 第五章 风险与不确定性分析

第五章风险与不确定性分析 §1盈亏平衡分析 一、 线性盈亏平衡分析 同理,还可求出其他因素的B印。如达到设计生产能力时,产品销售价 格的盈亏平衡点为: BEP (P)= +v+ 单位产品变动成本的盈亏平衡点: BEP ()=P-T-0
§1 盈亏平衡分析 一、线性盈亏平衡分析 同理,还可求出其他因素的BEP。如达到设计生产能力时,产品销售价 格的盈亏平衡点为: 第五章 风险与不确定性分析 V T Q F BEP ( P ) = + + 单位产品变动成本的盈亏平衡点: Q F BEP (v ) = P - T -

第五章风险与不确定性分析 一、 线性盈亏平衡分析 线性盈亏平衡分析的假设条件: (1)生产量等于销售量 (2)生产量变化,单位可变成本不变,从而使总生产成本成为生产 量的线性函数 (3)生产量变化,销售单价不变,从而是销售收入成为销售量的线 性函数 (4)只生产单一产品,或者生产多种产品,但是可以换算为单一产 品计算
一、线性盈亏平衡分析 线性盈亏平衡分析的假设条件: (1)生产量等于销售量 (2)生产量变化,单位可变成本不变,从而使总生产成本成为生产 量的线性函数 (3)生产量变化,销售单价不变,从而是销售收入成为销售量的线 性函数 (4)只生产单一产品,或者生产多种产品,但是可以换算为单一产 品计算。 第五章 风险与不确定性分析

第五章风险与不确定性分析 一-★ -一一一 例:某项目设计生产能力为年产50万件,根据资料分析,估计单 位产品价格为100元,单位产品可变成本为80元,固定成本为 30万元。已知该产品销售税金及附加合并税率为5%。现有一 客户前来订货25万件,问是否应该签订订货合同?并求项目 在盈亏平衡点的生产能力利用率。 解: E 3000000 =200000(件) P-t-V 100-100×5%-80 盈亏平衡点生产能力利用率为: E= g×100%= 200000 ×100%=40% 500000 由于订货25万件大于盈亏平衡产量20万件, 因此项目盈利,可以接受订单
例:某项目设计生产能力为年产50万件,根据资料分析,估计单 位产品价格为100元,单位产品可变成本为80元,固定成本为 30万元。已知该产品销售税金及附加合并税率为5%。现有一 客户前来订货25万件,问是否应该签订订货合同?并求项目 在盈亏平衡点的生产能力利用率。 解: 200000( ) 100 100 5% 80 * 3000000 = 件 - ´ - = - - = C c P t V F Q 盈亏平衡点生产能力利用率为: 由于订货25万件大于盈亏平衡产量20万件, 因此项目盈利,可以接受订单。 100% 40% 500000 200000 100% * * = ´ = ´ = QC Q E 第五章 风险与不确定性分析
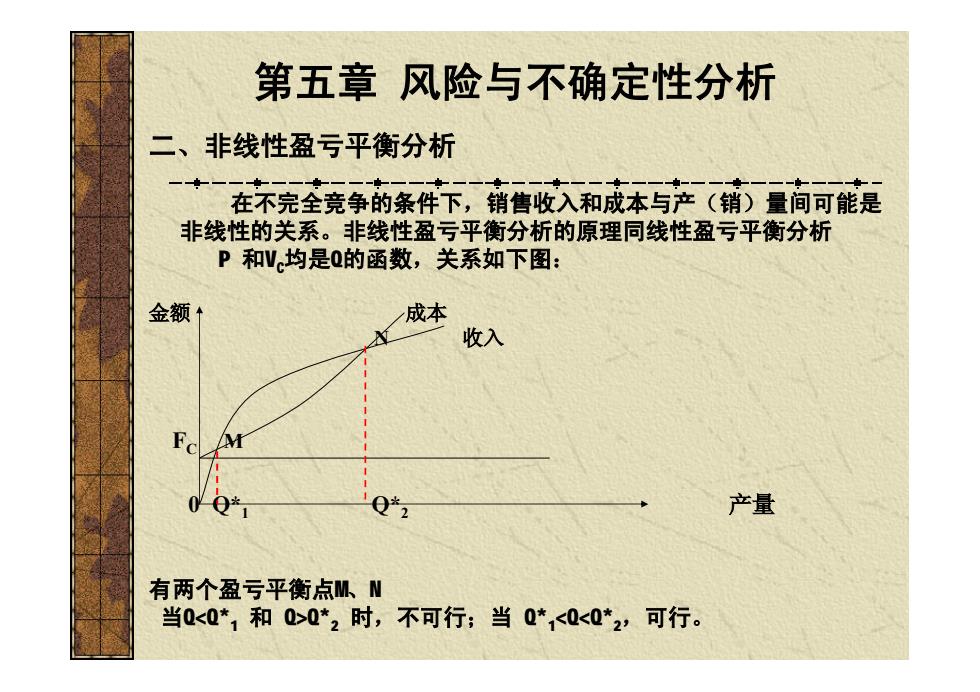
第五章风险与不确定性分析 二、非线性盈亏平衡分析 一一 在不完全竞争的条件下,销售收入和成本与产(销)量间可能是 非线性的关系。非线性盈亏平衡分析的原理同线性盈亏平衡分析 P和V均是Q的函数,关系如下图: 金额1 成本 收入 Q*2 产量 有两个盈亏平衡点M、N 当0<Q*1和0>0*2时,不可行;当Q*<0<0*2,可行
二、非线性盈亏平衡分析 在不完全竞争的条件下,销售收入和成本与产(销)量间可能是 非线性的关系。非线性盈亏平衡分析的原理同线性盈亏平衡分析 P 和VC均是Q的函数,关系如下图: 金额 成本 N 收入 FC M 0 Q*1 Q*2 产量 有两个盈亏平衡点M、N 当Q<Q*1 和 Q>Q*2 时,不可行;当 Q*1 <Q<Q*2,可行。 第五章 风险与不确定性分析