
7.5塔的强度设计 过程设备设计 根据牛顿第二定律,梁上的分布惯性力q为 02y g=-m (7-2) ∂t2 式中m一塔单位高度上的质量,kgm。 将式(7-2)代入式(7-1)得 ∂4y+m ∂2y dx4 EI 0t2 0 (7-3) 13
7.5 塔的强度设计 过程设备设计 2 2 t y q m ∂∂ = − 根据牛顿第二定律,梁上的分布惯性力 ,梁上的分布惯性力q为 (7-2) 式中 m─塔单位高度上的质量,kg/m。 将式(7-2)代入式(7-1)得 13 将式(7-2)代入式(7-1)得 0 2 2 4 4 = ∂ ∂ + ∂ ∂ t y EI m x y (7-3)

7.5塔的强度设计 过程设备设计 根据塔的振动特性,令上式的解为 通解 y(x,t)=Y(x)sin(at+o) 式中o-塔的固有圆频率,rad/s; t-时间,s Y(x一塔振动时在x处的最大位移,m。 14
7.5 塔的强度设计 过程设备设计 y(x,t) = Y (x)sin(ωt +ϕ) 根据塔的振动特性,令上式的解为 ,令上式的解为 式中 ω─塔的固有圆频率,rad/s; 通解 14 式中 ω─塔的固有圆频率,rad/s; t─时间,s; Y(x)─塔振动时在x处的最大位移,m
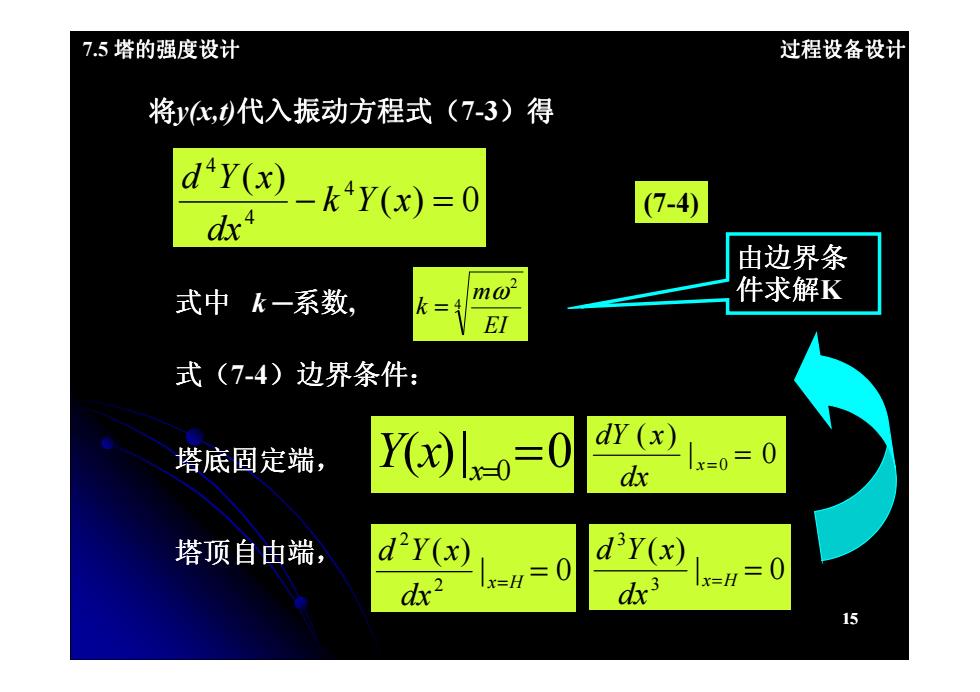
7.5塔的强度设计 过程设备设计 将y化,)代入振动方程式(7-3)得 d'Y(x 2-k4Y(x)=0 (7-4) dx 由边界条 式中k一系数 件求解K k二 ma2 El 式(7-4)边界条件: 塔底固定端, Y儿o=0 dx 塔顶自由端, d2Y(x) dY(x) dx2 x=H0 dx3 x=H=0 15
7.5 塔的强度设计 过程设备设计 ( ) 0 ( ) 4 4 4 − k Y x = dx d Y x 将y(x,t)代入振动方程式(7-3)得 (7-4) 4 2 EI m k ω 式中 k ─系数, = 由边界条 件求解K 15 | 0 ( ) x =0 = dx dY x 式(7-4)边界条件: | 0 ( ) 2 2 x=H = dx d Y x | 0 ( ) 3 3 x=H = dx 塔顶自由端, d Y x 塔底固定端, Y(x |) x=0=0

7.5塔的强度设计 过程设备设计 求解此方程得塔设备前三个振型时的k值分别为: 1.875 H 4.694 k2 H 7.855 k3 三 H 16
7.5 塔的强度设计 过程设备设计 求解此方程得塔设备前三个振型时的k值分别为: H k 1 . 875 1 = 4 . 694 16 H k 4 . 694 2 = H k 7 . 855 3 =
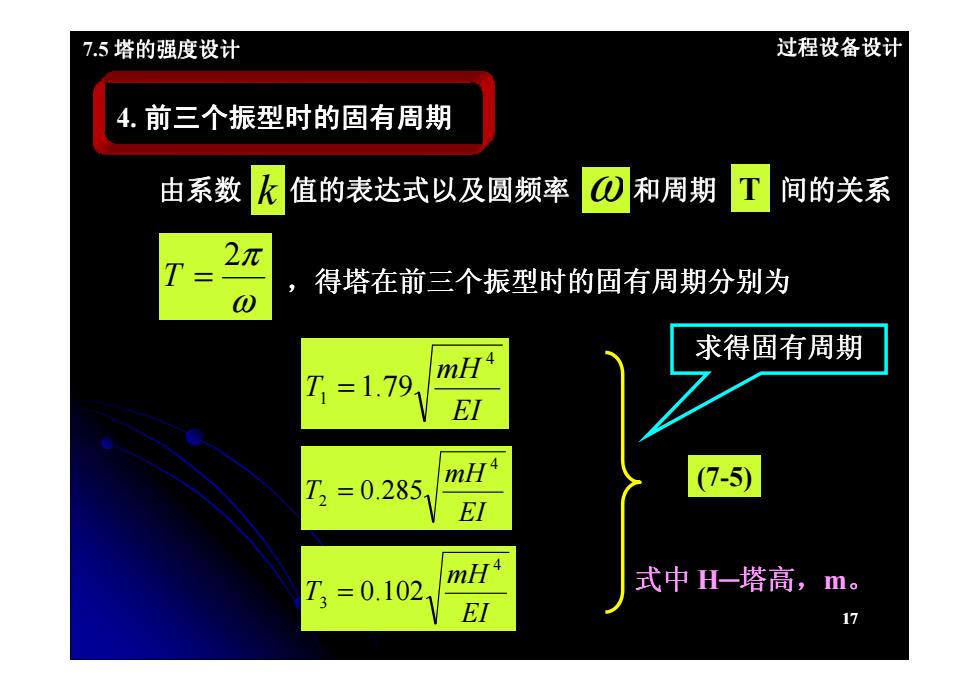
7.5塔的强度设计 过程设备设计 4.前三个振型时的固有周期 由系数 值的表达式以及圆频率 和周期 T 间的关系 2元 得塔在前三个振型时的固有周期分别为 求得固有周期 T=1.79 El T2=0.285 7-5) El T3=0.102 式中H-塔高,m。 17
7.5 塔的强度设计 过程设备设计 4. 前三个振型时的固有周期 ω 2π T = 由系数 值的表达式以及圆频率 和周期 间的关系 ,得塔在前三个振型时的固有周期分别为 ,得塔在前三个振型时的固有周期分别为 k ω 求得固有周期 T 17 EI mH T 4 1 = .1 79 EI mH T 4 2 = .0 285 EI mH T 4 3 = .0 102 (7-5) 式中 H─塔高,m。 求得固有周期