
.4 一上海证券综合指数收益率 .3 2 .1 .2 1996 1998 2000 2002 2004 2006 2008 2010 2012 2014
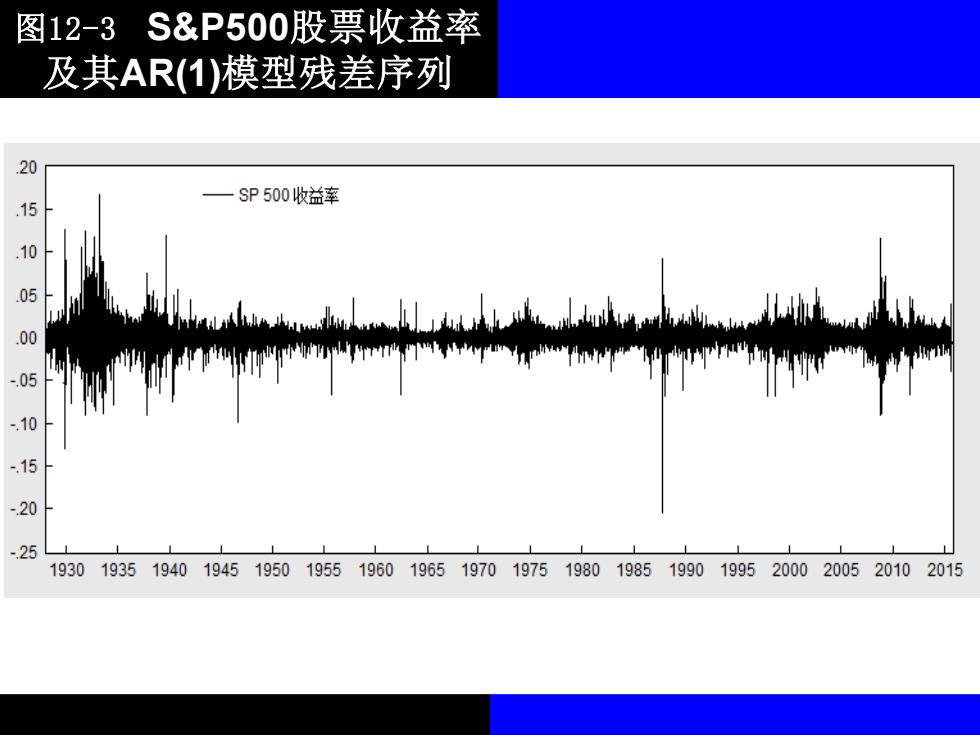
图12-3S&P500股票收益率 及其AR(1)模型残差序列 20 一SP500收益率 .10 .05 .00 -.05 -10 -15 -20 -25 193019351940194519501955196019651970197519801985199019952000200520102015
图12-3 S&P500股票收益率 及其AR(1)模型残差序列
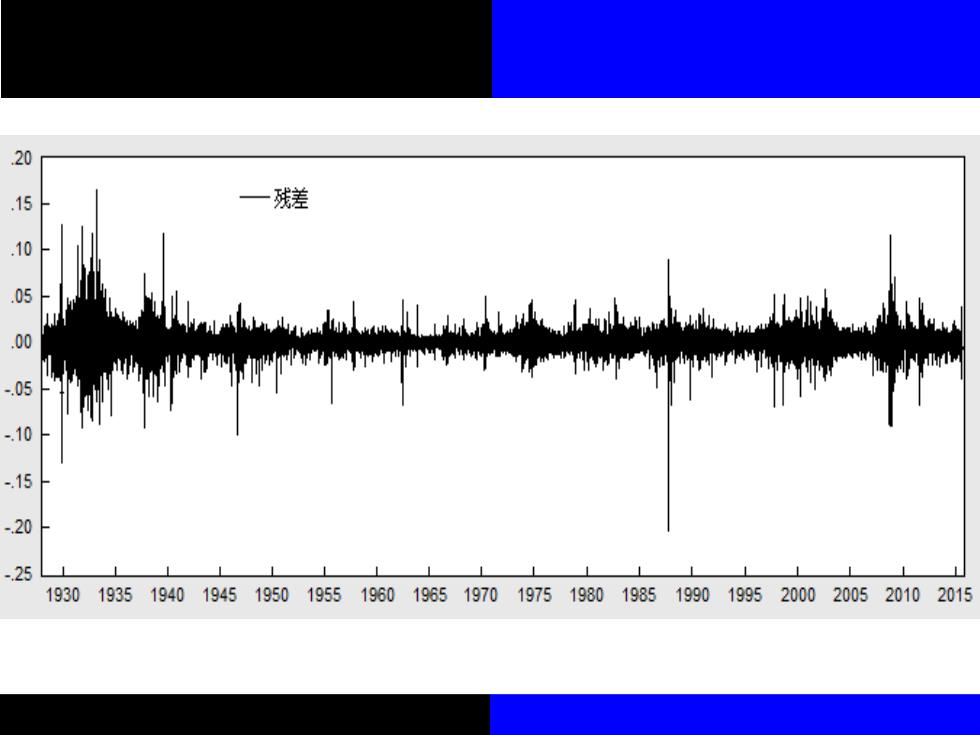
15 一残差 05 Ld .00 .05 .10 -20 25 193019351940194519501955196019651970197519801985199019952000200520102015

12.2 ARCH模型 12.2.1ARCH模型的定义 ARCH模型的核心思想是,误差项在 时刻t的方差依赖于时刻t-1的误差平方 的大小。因此,在ARCH建模的过程中, 要涉及到两个核心的模型回归过程,即 原始的回归模型(常被称为条件均值回 归模型)和方差的回归模型(条件异方 差回归模型)
12.2 ARCH模型 12.2.1 ARCH模型的定义 ARCH模型的核心思想是,误差项在 时刻t的方差依赖于时刻t−1的误差平方 的大小。因此,在ARCH建模的过程中, 要涉及到两个核心的模型回归过程,即 原始的回归模型(常被称为条件均值回 归模型)和方差的回归模型(条件异方 差回归模型)

ARCH(1)模型的基本组成形式: 4=x0+4,4~N0,G) (12.1) o =E(u) (12.2) =0%+c44 其中:y,和x,分别表示因变量和自变量,4 表示无序列相关性的随机扰动项。σ表示 在t时刻随机扰动项的方差,因为方差随 时间变化,并且以过去的扰动项的信息 为变化条件,所以称为“条件异方差
ARCH(1)模型的基本组成形式: (12.1) (12.2) 其中: 和 分别表示因变量和自变量, 表示无序列相关性的随机扰动项。 表示 在t时刻随机扰动项的方差,因为方差随 时间变化,并且以过去的扰动项的信息 为变化条件,所以称为“条件异方差”。 t y t x t u 2 t