《电磁场与电磁波》课程教学资源（PPT课件）第二章 电磁场的基本规律

2.电场强度 电场强度矢量卫一描述电场分布的基本物理量 空间某点的电场强度定义为置于该点的单位点电荷（又称试 验电荷)受到的作用力，即 E()=lim FF) 9o一试验正电荷 90→>0 90 根据上述定义，真空中静止点电 荷g激发的电场为 M E(T)= gR (R=r-) 4πe,R3 如果电荷是连续分布呢？ 2005-1-25 第一章电磁场的数学物理基础 21

2005-1-25 第一章 电磁场的数学物理基础 21 2. 电场强度 空间某点的电场强度定义为置于该点的单位点电荷（又称试 验电荷）受到的作用力，即 0 0 ( ) ( ) lim 0 q F r E r q     → = 3 0 4π ( ) R qR E r     = 如果电荷是连续分布呢？ 根据上述定义，真空中静止点电 荷q 激发的电场为 ( ) R r r = −  电场强度矢量 E—— 描述电场分布的基本物理量 0 q ——试验正电荷 y x z o r  q r R E M

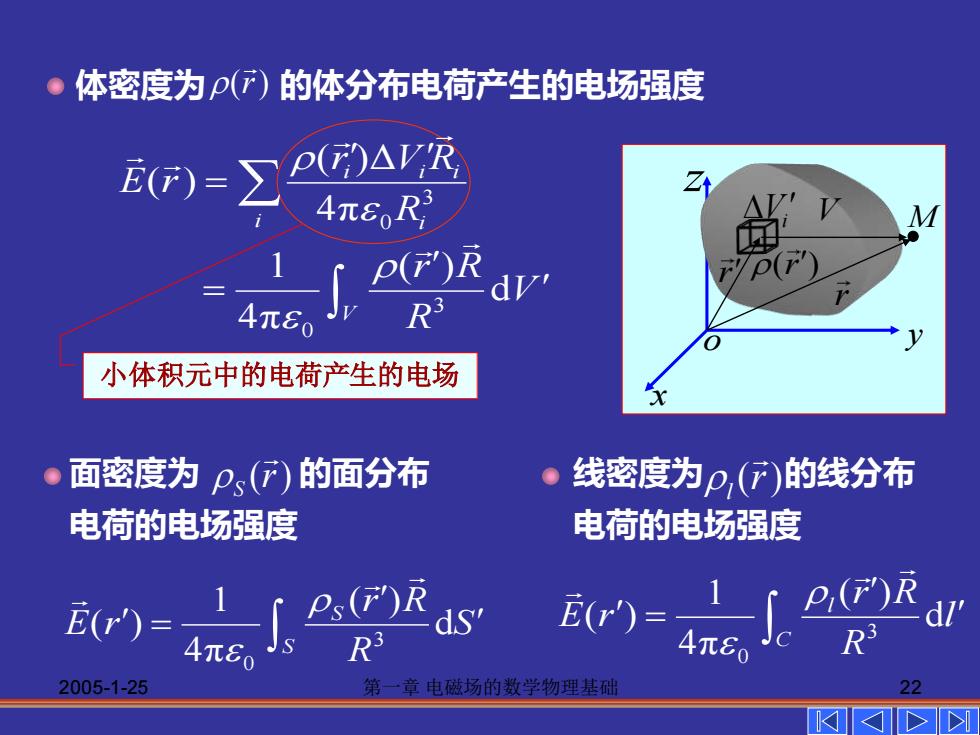
●体密度为ρ()的体分布电荷产生的电场强度 E)=∑ p(⑦)AR 4π8，R M P(F) -av' 4元80 R3 1) 小体积元中的电荷产生的电场 ·面密度为ps()的面分布 ·线密度为p,()的线分布 电荷的电场强度 电荷的电场强度 E(r)= Ps(F) ds E(r'）= -I 4元80 R3 R3 2005-1-25 第一章电磁场的数学物理基础 >>I

2005-1-25 第一章 电磁场的数学物理基础 22 小体积元中的电荷产生的电场 ( ) r  V y x z o r  Vi   r M (r) S  面密度为  的面分布 电荷的电场强度 (r) l  线密度为  的线分布 电荷的电场强度 体密度为 (r) 的体分布电荷产生的电场强度      = i i i i i R r V R E r 3 4π 0 ( )Δ ( )          = V V R r R d ( ) 4π 1 3 0         = S S S R r R E r d ( ) 4π 1 ( ) 3 0          = C l l R r R E r d ( ) 4π 1 ( ) 3 0     

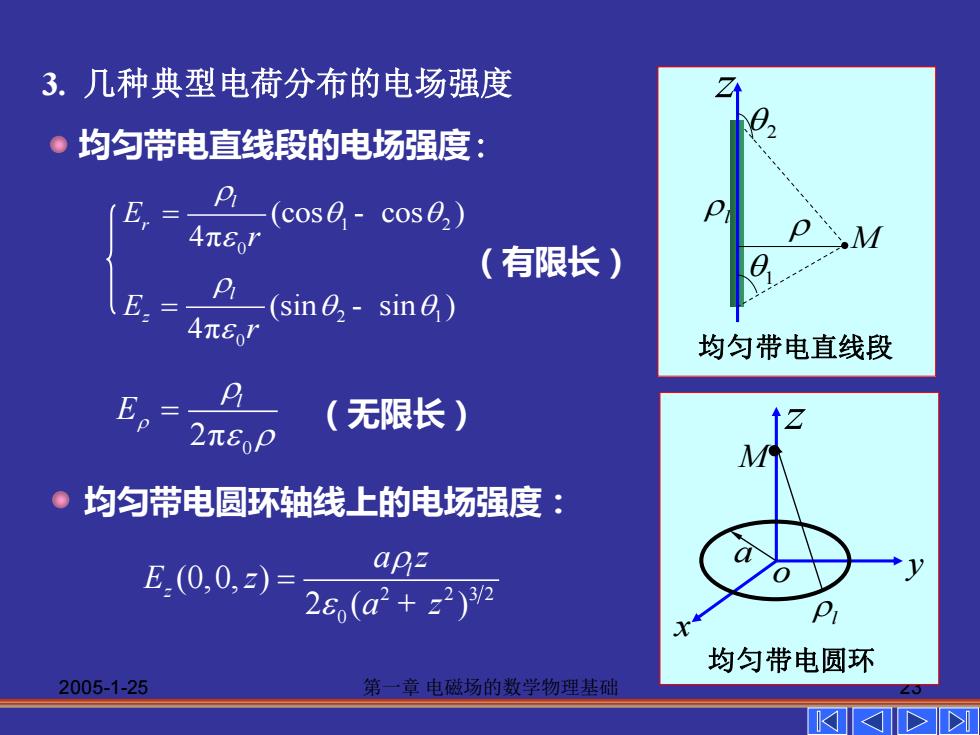
3.几种典型电荷分布的电场强度 。均匀带电直线段的电场强度： (E.= (cose-cose2) 4元8r (有限长) E,二 (sine-sin) 4元8I 均匀带电直线段 Ep (无限长) 2元8P 。均匀带电圆环轴线上的电场强度： E.(0,0,z)= apz 28(ad2+z22 均匀带电圆环 2005-1-25 第一章电磁场的数学物理基础

2005-1-25 第一章 电磁场的数学物理基础 23 3. 几种典型电荷分布的电场强度 0 2π l E    = 2 2 3 2 0 (0,0, ) 2 ( ) l z a z E z a z   = + （无限长） （有限长） l y x z o M a 均匀带电圆环 l 1  z M 2 均匀带电直线段 均匀带电直线段的电场强度： 均匀带电圆环轴线上的电场强度： 1 2 0 2 1 0 (cos cos ) 4π (sin sin ) 4π l l z E E         = = r r r - -

电偶极子的电场强度： 电偶极子是由相距很近、带等值异号的两个点电荷组成的电 荷系统，其远区电场强度为 B)=,L「 4π8r' p=gl —电偶极矩 电场线 等位线 电偶极子 2005 电磁场的数学物 电偶极子的场图

2005-1-25 第一章 电磁场的数学物理基础 24 ( ) 5 3 3 0 0 1 3( ) ( ) 2cos sin 4π 4π r p r r p P E r e e r r r         = − = +     p ql = ——电偶极矩  r E +q 电偶极子 z l o －q 电偶极子的场图 等位线 电场线 电偶极子是由相距很近、带等值异号的两个点电荷组成的电 荷系统，其远区电场强度为 电偶极子的电场强度：

例2.2.1计算均匀带电的环形薄圆盘轴线上任意点的电场强 度。 解：如图所示，环形薄圆盘的内半径为4、外半径为b,电荷 面密度为Ps。在环形薄圆盘上取面积元 de dS'=p'dp'dp,其位置矢量为产=eA P(0,0,2) 它所带的电量为dg=P,dS'=Psp'dp'd。 而薄圆盘轴线上的场点P(0,0,z)的位置 矢量为下=e:,因此有 ds =Iewaw 均匀带电的环形薄圆盘 由于 e,d="ecos+e,sin)d"=0 故 p'dp =e图 2005-1-25 (e2+a2)2 (22+b)0 M>☒

2005-1-25 第一章 电磁场的数学物理基础 25 例 2.2.1 计算均匀带电的环形薄圆盘轴线上任意点的电场强 度。 解：如图所示，环形薄圆盘的内半径为a 、外半径为b，电荷 面密度为 。在环形薄圆盘上取面积元 ，其位置矢量为 ， 它所带的电量为 。 而薄圆盘轴线上的场点 的位置 矢量为 ，因此有 S d ' 'd 'd ' S =  r e   =   d d ' 'd 'd ' S S q S = =      P z (0,0, ) z r e z = 2π 2 2 3/ 2 0 0 ( ) d d 4π ( ) b S z a e z e E r z       −  =    +    P(0,0,z) b r R y z x 均匀带电的环形薄圆盘 dS  a dE 2π 2π 0 0 d cos sin )d 0      x y     = + =   e (e e 故 2 2 3/ 2 2 2 1/ 2 2 2 1/ 2 0 0 d 1 1 ( ) 2 ( ) 2 ( ) ( ) b S S z z a z z z z a z b            = = −   + + +     E r e e 由于