《电磁场理论》课程电子教案（讲义）第六章 均匀平面波的反射和透射

第6章均匀平面波的反射与透射 现象：电磁波入射到不同媒质分界面上时，一部分波被分界面反射，一部分波透过分界面。 入射方式：垂直入射、斜入射： 媒质类型：理想导体、理想介质、导电媒质 分析方法： 边界条件 入射波（已知）+反射波（未知） 透射波（未知） 本章内容 6.1均匀平面波对分界面的垂直入射 介质分界面 6.2均匀平面波对多层介质分界平面的垂直入射 6.3均匀平面波对理想介质分界平面的斜入射 6.4均匀平面波对理想导体表面的斜入射 6.1 均匀平面波对分界平面的垂直入射 本节内容 6.1.1对导电媒质分界面的垂直入射 6.1.2对理想导体表面的垂直入射 6.13对理想介质分界面的垂直入射 媒质1 某质2 6.1.1对导电媒质分界面的垂直入射 z<0中，导电媒质1的参数为小外可 均匀平面波垂直入射到两种不 z>0中，导电媒质2的参数为凸620 沿x方向极化的均匀平面波从媒质1垂直入射到与导电媒质2的分界平面上。 媒质1中的入射波 E(=)=&Ee-n Y=jkie =jouSve ne)-e系e =jo√46(1-j)h 媒质 8,4,01 媒质1中的反射波： E,(=)=iEen 30) H0+ H0◆ =n0-c 媒质1中的合成波： E(=)=E,(=)+E(=)=,Eme-ni +,Emen 月e=月，(e)+,(e)=8, 媒质2中的透射波：

1 第6章 均匀平面波的反射与透射 现象：电磁波入射到不同媒质分界面上时，一部分波被分界面反射，一部分波透过分界面。 入射方式：垂直入射、斜入射； 媒质类型：理想导体、理想介质、导电媒质 分析方法： 入射波（已知）＋反射波（未知） 透射波（未知） 本章内容 6.1 均匀平面波对分界面的垂直入射 6.2 均匀平面波对多层介质分界平面的垂直入射 6.3 均匀平面波对理想介质分界平面的斜入射 6.4 均匀平面波对理想导体表面的斜入射 6.1 均匀平面波对分界平面的垂直入射 本节内容 6.1.1 对导电媒质分界面的垂直入射 6.1.2 对理想导体表面的垂直入射 6.1.3 对理想介质分界面的垂直入射 6.1.1 对导电媒质分界面的垂直入射 z < 0 中，导电媒质 1 的参数为 1 1 1 、 、 z > 0 中，导电媒质 2 的参数为 2 2  2  、 、 沿 x 方向极化的均匀平面波从媒质 1 垂直入射到与导电媒质 2 的分界平面上。 媒质 1 中的入射波 1 1 i im im i 1c ( ) e ( ) e z x z y E z e E E H z e    − − = = 1 1c 1 1c 1 1 2 1 1 1 j j j (1 j )     k      = = = − 媒质 1 中的反射波： 1 1 r rm rm r 1c ( ) e ( ) e z x z y E z e E E H z e    = = − 1 1 1 1 2 1c 1c 1 1 1 1 2 1 1 (1 j ) (1 j )           − − = = − = − 媒质 1 中的合成波： 1 1 1 1 1 i r im rm im rm 1 i r 1c 1c ( ) ( ) ( ) e e ( ) ( ) ( ) e e z z x x z z y y E z E z E z e E e E E E H z H z H z e e       − − = + = + = + = − 媒质 2 中的透射波： 边界条件 均匀平面波垂直入射到两种不 同媒质的分界平面 入射波 反射波 介质分界面 Ei i k Er Hi Hr r k o z y x 媒质 1 媒质 2 Et Ht t k 透射波 z x 媒 质 1： 媒 质 2： 1 1 1  , , 2 2 2  , , y Ei Hi i k Er Hr r k Et Ht t k

B.(=)=e,Eue-n H()=Eum e 为=k.=jo6=jog0-j 1-j%=m0-j0 V62 06, 在分界面z=0上，电场强度和磁场强度切向分量连续，即 E(0)=E,(0) 「Em+Em=Em H1(0)=H2(0) 定义分界面上的反射系数「为反射波电场的振幅与入射波电场振幅之比、透射系数π为透射 波电场的振幅与入射波电场振幅之比，则 I=Em=the-the Em+Em=Em Eim nc+me 1(E-E)= 72c Eim n2e+me 讨论： (1)1+Γ=x (2)「和π是复数，表明反射波和透射波的振幅和相位与入射波都不同。 (6)若媒质2为理想导体，即0，=0，则。=0，故有「=-小、t=0 =h-1 272 ,T三 ④若两种媒质均为理想介质，即=0，=0，则得到 2+ 2+7 6.1.2对理想导体表面的垂直入射 媒质1为理想介质，G,=0 在分界面上，反 馨题 射波电场与入射 媒质2为理想导体，02=0 被电场的相位差 为 则月=@4, Vs'n=0 =-1、t=0 Em=-E Z=0

2 2 2 tm t tm t 2c ( ) e , ( ) e z z x y E E z e E H z e    − − = = 2 1 2 2 2c 2 2c 2 2 2 j j j (1 j ) k          = = = − 2 2 2 2 1 2 1 2 2c 2 2c 2 2 2 (1 j ) (1 j )           − − = = − = − 在分界面 z = 0 上，电场强度和磁场强度切向分量连续，即 定义分界面上的反射系数  为反射波电场的振幅与入射波电场振幅之比、透射系数  为透射 波电场的振幅与入射波电场振幅之比，则 讨论： (1) 1+ = (2)  和  是复数，表明反射波和透射波的振幅和相位与入射波都不同。 (3) 若媒质 2 为理想导体，即  2 =  ，则 2c = 0 ，故有  = −1、 = 0 (4) 若两种媒质均为理想介质，即 1 = 2 = 0 ，则得到 2 1 2 2 1 2 1 2 ,          − = = + + 6.1.2 对理想导体表面的垂直入射 媒质 1 为理想介质， 1 = 0 媒质 2 为理想导体，  2 =  则 1 1 1     = , 1 1 1 ,    = 2 = 0 故  = −1、 = 0 E E rm im = − (0) (0) (0) (0) 1 2 1 2 H H E E =  =   im rm tm im rm tm 1c 2c 1 1 ( ) E E E E E E   + = − =    im rm tm im rm tm 1c 2c 1 1 ( ) E E E E E E   + = − =    tm 2c im 2c 1c E 2 E     = = + rm 2c 1c im 2c 1c E E      − = =  +   x 媒质 1： 媒质 2： 1 1 1  , ,  2 =  z z = 0 y Ei Hi i k Er Hr r k 在分界面上，反 射波电场与入射 波电场的相位差 为π

E(e)=eEe,月(e)=eem 媒质1中的入射波： 7 B.(=)-,Eein:,F,(=)=8 Eme 媒质1中的反射波： 媒质1中合成波的电磁场为 E(=)=E(-)=-e,j2Em sin(B=) 月，（）日=E,5(e4+e4)=E,2 Em cosB 瞬时值形式 E(,t)=Re[E ()ei]=e.2E sin(B)sin(ot) i(e.)=Re[i,(（ee]=e2 cosp=pcos(or）) 合成波的平均能流密度矢量 5.-Re[ExHJ:]-Re-i.p2E.sin(Bz)xi, 2E cos(B=) 理想导体表面上的感应电流 xF()-.xg,2E cosE 合成波的特点 (1)媒质1中的合成波是驻波。电场振幅的最大值为2B,最小值为0，磁场振幅的最大值 为2E/n,最小值也为0。 (2)电场波节点，（以的最小值的位置） E 8=m→m=20123 (3)电场波腹点(E(的最大值的位置) 月m=-2m+m2a-2m+2 4 (0=0,1,2,3,)

3 媒质 1 中的入射波： 1 1 j j im i im i 1 ( ) e , ( ) e z z x y E E z e E H z e    − − = = 媒质 1 中的反射波： 1 1 j j im r im r 1 ( ) e , ( ) e z z x y E E z e E H z e    = − = 媒质 1 中合成波的电磁场为 1 1 1 1 j j 1 im im 1 im im 1 j j 1 1 1 ( ) (e e ) j2 sin( ) 2 cos( ) ( ) (e e ) z z x x z z y y E z e E e E z E E z H z e e         − − = − = − = + = 瞬时值形式 j 1 1 im 1 j im 1 1 1 1 ( , ) Re[ ( )e ] 2 sin( )sin( ) 2 ( , ) Re[ ( )e ] cos( )cos( ) t x t y E z t E z e E z t E H z t H z e z t        = = = = 合成波的平均能流密度矢量 * * im 1 av 1 1 im 1 1 1 1 2 cos( ) Re[ ] Re j2 sin( ) 0 2 2 x y E z S E H e E z e        =  = −  =           理想导体表面上的感应电流 im 1 im n 1 0 0 1 1 2 cos( ) 2 ( ) | | S z z y z x E z E J e H z e e e    =  = −  = = = 合成波的特点 （1）媒质 1 中的合成波是驻波。电场振幅的最大值为 2Eim ，最小值为 0 ；磁场振幅的最大值 为 2Eim 1 ，最小值也为 0。 （2）电场波节点（ E (z) 1 的最小值的位置） 1 min  z n = − π 1 min 2 n z  = − (n = 0 ,1,2,3, .) (3) 电场波腹点（ E (z) 1 的最大值的位置） 1 min  z n = − + (2 1)π / 2 1 max (2 1) 4 n z +  = − (n = 0 ,1,2,3, .)

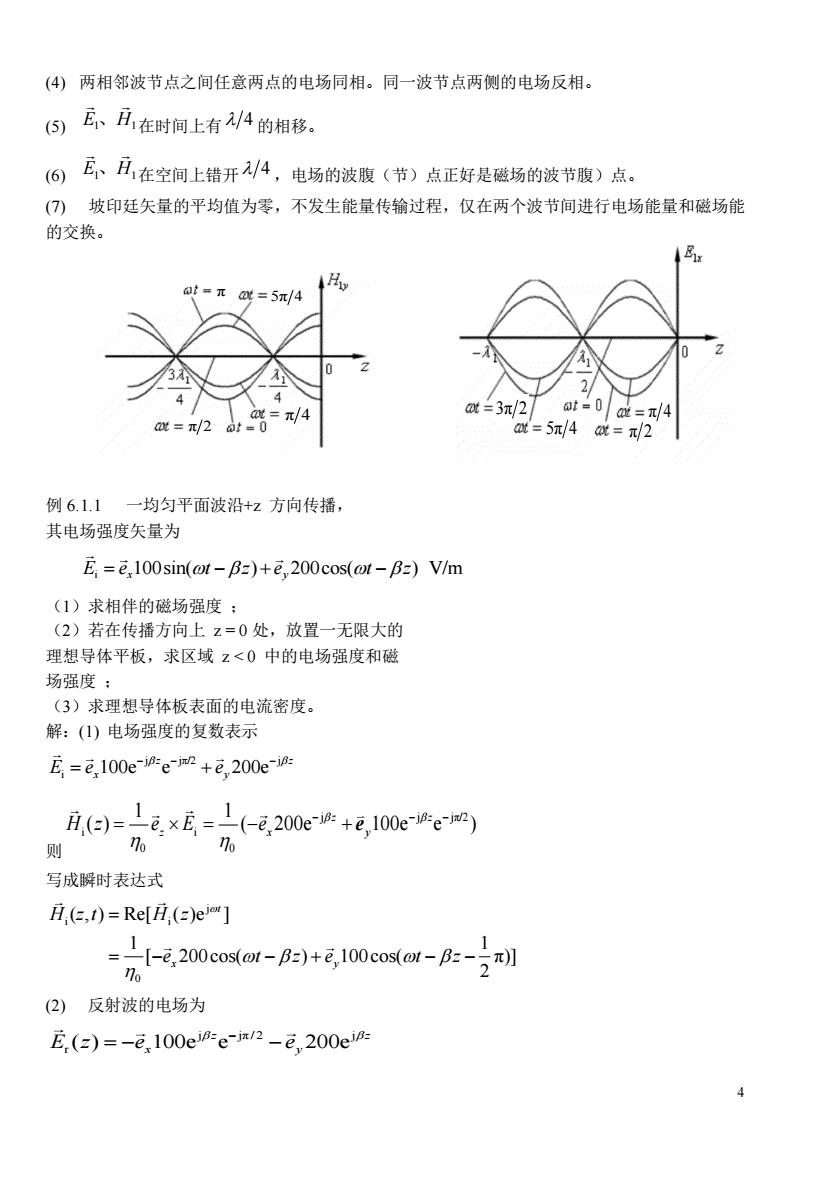
(4)两相邻波节点之间任意两点的电场同相。同一波节点两侧的电场反相。 (6)瓦月在时间上有4的相移。 6瓦月在空间上错开4，电场的波腹（节）点正好是磁场的波节腹)点。 ()坡印廷矢量的平均值为零，不发生能量传输过程，仅在两个波节间进行电场能量和磁场能 的交换。 =5π/4 =3元/27 a=5π/4=/2 例6.11一均匀平面波沿+z方向传播， 其电场强度矢量为 E=2,100sin(@t-B=)+e,200cos(@t-Bz)V/m (1)求相伴的磁场强度： (2)若在传播方向上z=0处，放置一无限大的 理想导体平板，求区域z<0中的电场强度和磁 场强度： (3)求理想导体板表面的电流密度。 解：()电场强度的复数表示 E =2,100e-i-e-+e200e-i- 月(e)=1e×E=1（←-e200e换+e,100eem) 则 %6 76 写成瞬时表达式 (,1)=Re[,(=)e] -2-e.20 Dcadot-B）时+e10eoom-8E-5 (2)反射波的电场为 E.(e)=-e,100e-e2-e,200er

4 (4) 两相邻波节点之间任意两点的电场同相。同一波节点两侧的电场反相。 (5) E1 H1   、 在时间上有  4 的相移。 (6) E1 H1   、 在空间上错开  4 ，电场的波腹（节）点正好是磁场的波节腹）点。 (7) 坡印廷矢量的平均值为零，不发生能量传输过程，仅在两个波节间进行电场能量和磁场能 的交换。 例 6.1.1 一均匀平面波沿+z 方向传播， 其电场强度矢量为 i E e t z e t z = − + − x y 100sin( ) 200cos( ) V/m     （1）求相伴的磁场强度 ； （2）若在传播方向上 z = 0 处，放置一无限大的 理想导体平板，求区域 z < 0 中的电场强度和磁 场强度 ； （3）求理想导体板表面的电流密度。 解：(1) 电场强度的复数表示 j jπ/2 j i 100e e 200e z z E e e x y − − −   = + 则 j j jπ/2 i i 0 0 1 1 ( ) ( 200e 100e e ) z z H z e E e z x y     − − − =  = − + e 写成瞬时表达式 j i i 0 ( , ) Re[ ( )e ] 1 1 [ 200cos( ) 100cos( π)] 2 t x y H z t H z e t z e t z       = = − − + − − (2) 反射波的电场为 j jπ/ 2 j r ( ) 100e e 200e z z E z e e x y   − = − − π2 5π 4 π π4 π 4 π 2 3π 2 5π 4 π 4 π 2 3π 2 5π 4

反射波的磁场为 i.(e)=1(-e.×E)=1（-e,200eie+e,100ee) 在区域z<0的合成波电场和磁场分别为 E=E+E=-&,j200e-/2 sin(B=)-&,j400sin(B=) 月，=月，+i=[-e,400cos(B=)+e,200 cs(B= (③)理想导体表面电流密度为 Js=-exHlm0 =e200e-:+ 400 =-ej0.53+e1.06 7% 6.1.3对理想介质分界面的垂直入射 设两种媒质均为理想介质，即01=02=0 Y=jB,=joyue 则为=j讽=j0W46 「=么-h 22 72+n 讨论 (1)当>1时，「>0，反射波电场与入射波电场同相。 (2)当h<几时，「<0，反射波电场与入射波电场反相。 E(=)=8,Ee 媒质1中的入射波： e-e会e

5 反射波的磁场为 j j jπ/ 2 r r 0 0 1 1 ( ) ( ) ( 200e 100e e ) z z H z e E e e z x y     − = −  = − + 在区域 z < 0 的合成波电场和磁场分别为 jπ/ 2 1 i r jπ/ 2 1 i r 0 j200e sin( ) j400sin( ) 1 [ 400cos( ) 200e cos( )] x y x y E E E e z e z H H H e z e z      − − = + = − − = + = − + (3) 理想导体表面电流密度为 S z z 1 0 J e H = −  = jπ/ 2 0 0 200 400 e j0.53 1.06 x y x y e e e e   − = + = − + 6.1.3 对理想介质分界面的垂直入射 设两种媒质均为理想介质，即 1 = 2 = 0 则 1 1 1 1 2 2 2 2 j j j j           = = = = 1 2 1c 1 2c 2 1 2 ,         = = = = 2 1 2 2 1 2 1 2 ,          − = = + + 讨论 （1）当 2 1 时，   0 ，反射波电场与入射波电场同相。 （2）当 2 1 时，   0 ，反射波电场与入射波电场反相。 媒质 1 中的入射波： 1 1 j i im j im i 1 ( ) e ( ) e z x z y E z e E E H z e    − − = = x 介 质 1： 介 质 1 1 2：  , 2 2  , z z= 0 y Ei Hi i k Er Hr r k Et Ht t k