
2.2.2静电场的散度与旋度 1.静电场散度与高斯定理 静电场的散度(微分形式) 静电场的高斯定理(积分形式) V.= fE()-ds=()dr C. 高斯定理表明:静电场是有源场,电力线起始于正电荷,终止 于负电荷。 2.静电场旋度与环路定理 静电场的旋度(微分形试) 静电场的环路定理(积分形试) V×E()=0 fE(F).d7=0 环路定理表明:静电场是无旋场,是保守场,电场力做功与路径 无关。 2005-1-25 第一章电磁场的数学物理基础 26
2005-1-25 第一章 电磁场的数学物理基础 26 2.2.2 静电场的散度与旋度 = S V E r S (r)dV 1 ( ) d 0 高斯定理表明:静电场是有源场,电力线起始于正电荷,终止 于负电荷。 静电场的散度(微分形式) 1. 静电场散度与高斯定理 静电场的高斯定理(积分形式) = E r( ) 0 环路定理表明:静电场是无旋场,是保守场,电场力做功与路径 无关。 静电场的旋度(微分形式) 2. 静电场旋度与环路定理 静电场的环路定理(积分形式) ( )d = 0 C E r l 0 ( ) ( ) r E r =

3.利用高斯定理计算电场强度 在电场分布具有一定对称性的情况下,可以利用高斯定理计 算电场强度。 具有以下几种对称性的场可用高斯定理求解: 球对称分布:包括均匀带电的球面,球体和多层同心球壳等。 R2 Po S2 带电球壳 多层同心球壳 均匀带电球体 2005-1-25 第一章电磁场的数学物理基础 21
2005-1-25 第一章 电磁场的数学物理基础 27 在电场分布具有一定对称性的情况下,可以利用高斯定理计 算电场强度。 3. 利用高斯定理计算电场强度 具有以下几种对称性的场可用高斯定理求解: • 球对称分布:包括均匀带电的球面,球体和多层同心球壳等。 带电球壳 多层同心球壳 均匀带电球体 a O ρ0
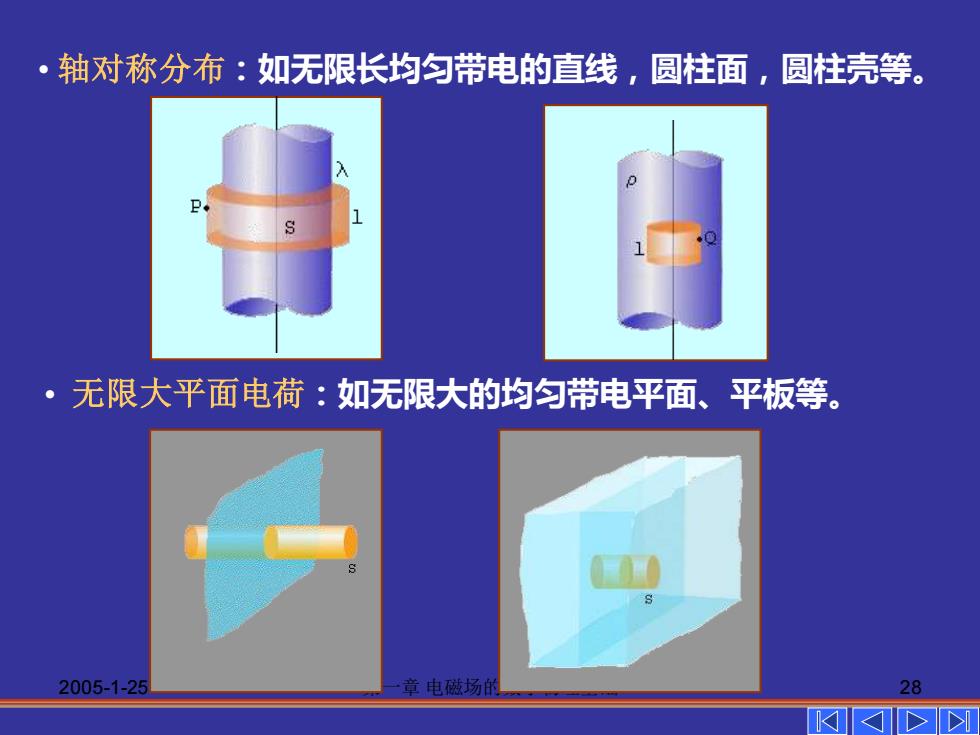
轴对称分布:如无限长均匀带电的直线,圆柱面,圆柱壳等。 ·无限大平面电荷:如无限大的均匀带电平面、平板等。 2005-1-25 章电磁场的 28
2005-1-25 第一章 电磁场的数学物理基础 28 • 无限大平面电荷:如无限大的均匀带电平面、平板等。 • 轴对称分布:如无限长均匀带电的直线,圆柱面,圆柱壳等

例2.2.2求真空中均匀带电球体的场强分布。已知球体半径 为a,电荷密度为po。 解:(1)球外某点的场强 由 fE.ds=9=14 元aPo 80 83 E= Poa 38, (r≥a) (2)求球体内一点的场强 由 fE-d5=,pdv 1 4π2E= 4 ,4ma33πr 9 E=Por 2005-1-25 360 (r<a) 第一章电磁场的数学物理基础 29 >
2005-1-25 第一章 电磁场的数学物理基础 29 例2.2.2 求真空中均匀带电球体的场强分布。已知球体半径 为a ,电 荷密度为 0 。 解:(1)球外某点的场强 0 3 0 0 π 3 1 4 d a q E S S = = (2)求球体内一点的场强 E S V S V = d 1 d 0 0 a r 0 r r E a 2 0 3 0 3 r a E = ( r ≥ a ) 3 3 0 2 π 3 4 4π 3 1 4 r a q r E = 0 0 3 r E = (r < a) 由 由

2.3真空中恒定磁场的基 本规律 本节内容 2.3.1安培力定律磁感应强度 2.3.2恒定磁场的散度与旋度 2005-1-25 第一章电磁场的数学物理基础 30
2005-1-25 第一章 电磁场的数学物理基础 30 2.3 真空中恒定磁场的基 本规律 本节内容 2.3.1 安培力定律 磁感应强度 2.3.2 恒定磁场的散度与旋度