
8协方差分析的模型和假定假定>协变量是非随机变量,没有度量误差>Y对协变量的回归是线性的,并且各处理内的回归系数是齐性的>随机误差服从正态分布N(O,α2),且互相独立6
6 协方差分析的模型和假定 ⚫假定 ➢协变量是非随机变量,没有度量误差 ➢Y 对协变量的回归是线性的,并且各处理内 的回归系数是齐性的 ➢随机误差服从正态分布 ,且互相 独立
BIES单向分类资料的协方差分析例12-1:3种饲料的增重效果比较试验饲料平均初始重(X)/日增重(Y)(kg)X151311121216141713.75A1Y0.910.820.850.830.650.760.800.840.902219X17161818211818.63A2Y0.980.970.901.000.951.031.060.990.94X222420232527303225.38A3Y0.890.910.830.951.100.971.001.021.05
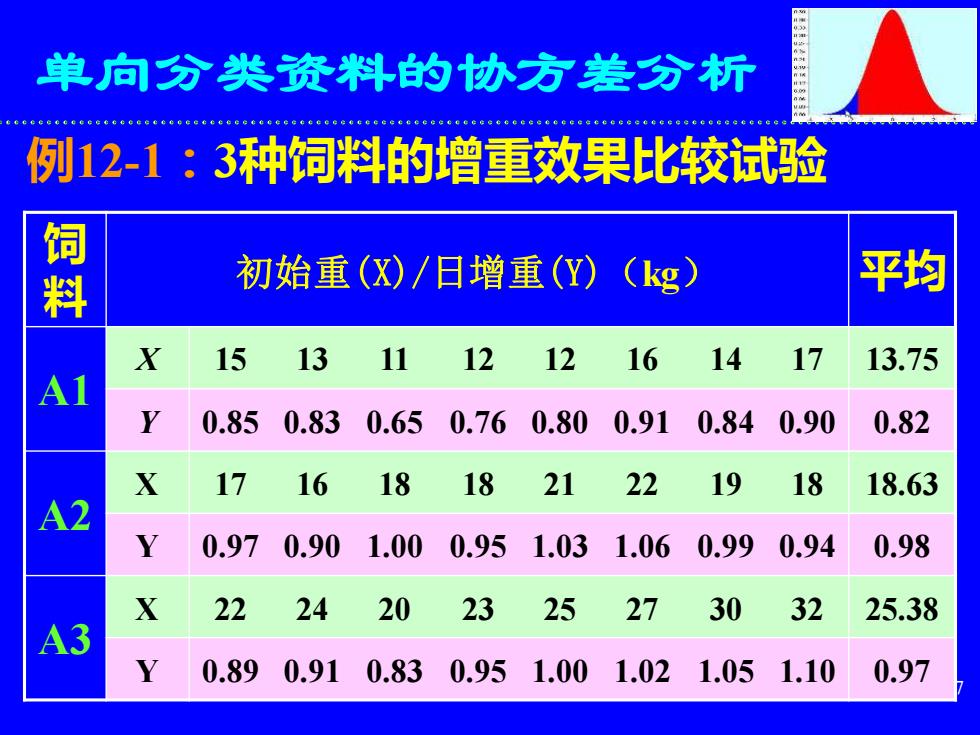
7 单向分类资料的协方差分析 例12-1:3种饲料的增重效果比较试验 饲 料 初始重(X)/日增重(Y)(kg) 平均 A1 X 15 13 11 12 12 16 14 17 13.75 Y 0.85 0.83 0.65 0.76 0.80 0.91 0.84 0.90 0.82 A2 X 17 16 18 18 21 22 19 18 18.63 Y 0.97 0.90 1.00 0.95 1.03 1.06 0.99 0.94 0.98 A3 X 22 24 20 23 25 27 30 32 25.38 Y 0.89 0.91 0.83 0.95 1.00 1.02 1.05 1.10 0.97
BS单向分类资料的协方差分析●不考虑初重,对日增重的方差分析变异均方平方和自由度F来源饲料211.17**0.13180.0659误差210.12380.0059总和230.2556F0.01(2, 21) = 5.788
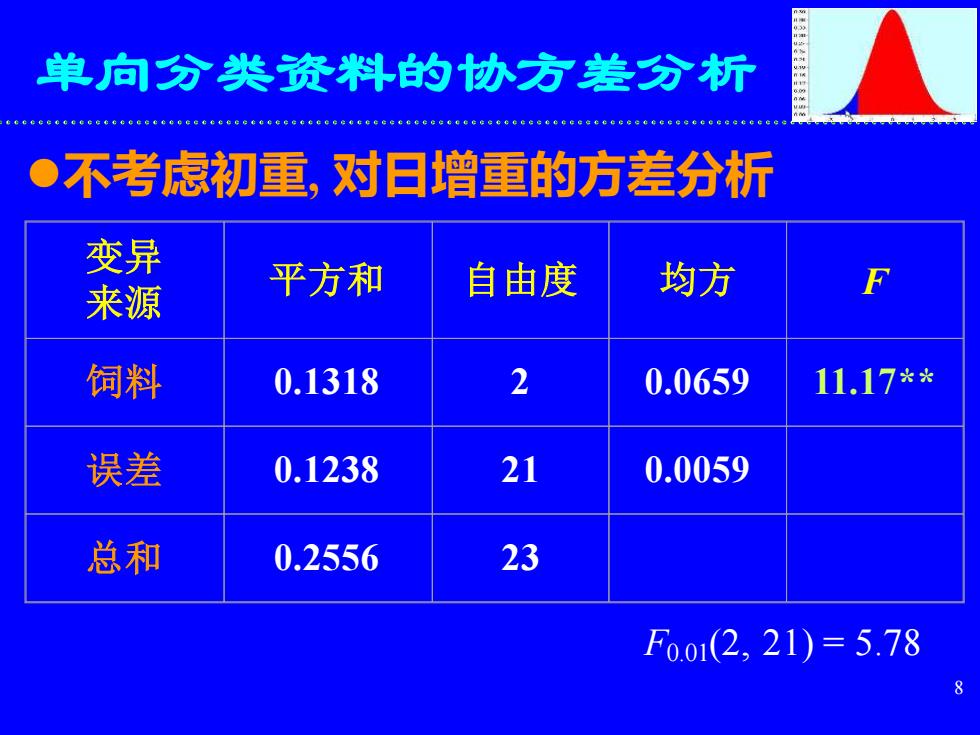
8 单向分类资料的协方差分析 ⚫不考虑初重, 对日增重的方差分析 变异 来源 平方和 自由度 均方 F 饲料 0.1318 2 0.0659 11.17** 误差 0.1238 21 0.0059 总和 0.2556 23 F0.01(2, 21) = 5.78