《畜牧生物统计与实验设计》课程授课教案（PPT讲稿）第十章 多元线性回归与相关

第十章多元线性回归与相关多元线性回归的数学模型多元线性回归的建立多元线性回归的检验复相关与偏相关

第十章 多元线性回归与相关 ⚫多元线性回归的数学模型 ⚫多元线性回归的建立 ⚫多元线性回归的检验 ⚫复相关与偏相关

1TE8多元回归分析的意义研究随机变量对多个自变量的回归关系主要自的：利用回归方程对依变量的取值进行估计和预测·例：>牛的体重与体长和胸围>猪的瘦肉率与背厚和眼肌面积

2 多元回归分析的意义 ⚫研究随机变量对多个自变量的回归关系 ⚫主要目的：利用回归方程对依变量的取值 进行估计和预测 ⚫例： ➢牛的体重与体长和胸围 ➢猪的瘦肉率与背膘厚和眼肌面积

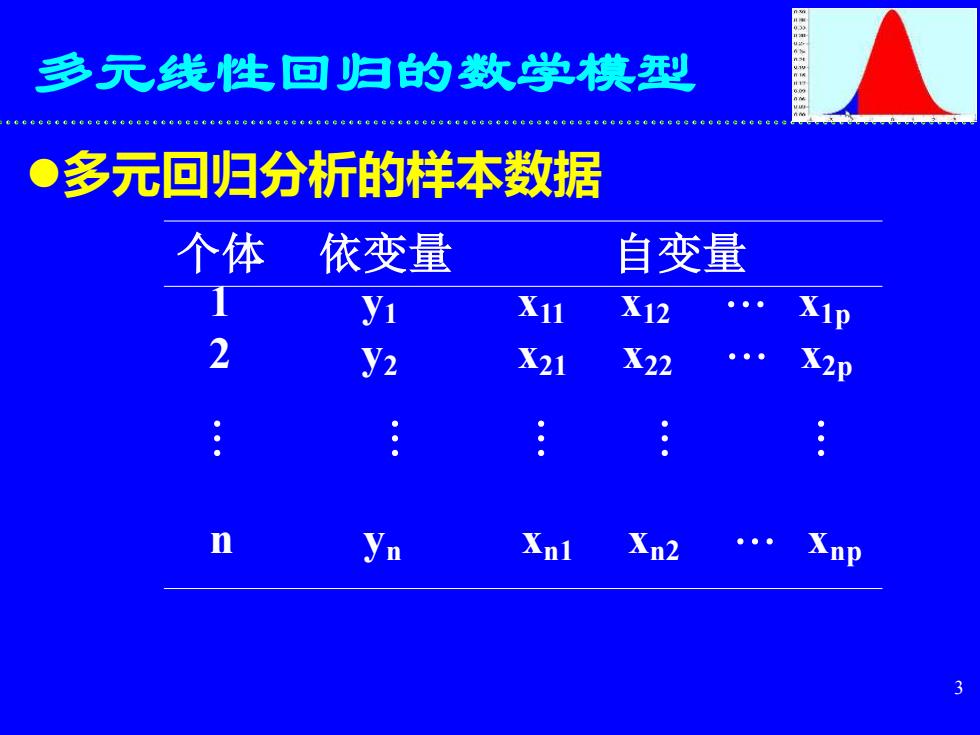
S多元线性回归的数学模型eeeeeeee●多元回归分析的样本数据个体依变量自变量1X1lY1X12Xip2Y2X21X22X2pnXnlynXn2Xnp?3

3 多元线性回归的数学模型 ⚫多元回归分析的样本数据 个体 依变量 自变量 1 y1 x11 x12  x1p 2 y2 x21 x22  x2p      n yn xn1 xn2  xnp

EARAATPEESE多元线性回归的数学模型Yi =βo +βiXi1 +β2Xi2 +...+βpXip +eii=1,2,, n回归参数βo:常数项β:偏回归系数(j=l,2,p)当其他自变量保持不变时，自变量x;每改变1个单位所造成的V的变化量ei：随机误差ei ~ N(0,α2)各个e彼此独立

4 多元线性回归的数学模型 i i i p ip i y =  + x + x ++ x +e 0 1 1 2 2 i = 1, 2, , n 0: 常数项 j : 偏回归系数（j = 1, 2, , p） 当其他自变量保持不变时，自变量 xj 每 改变1个单位所造成的 y 的变化量 ei : 随机误差 ~ (0, ) 2 ei N  各个ei彼此独立 回  归 参 数

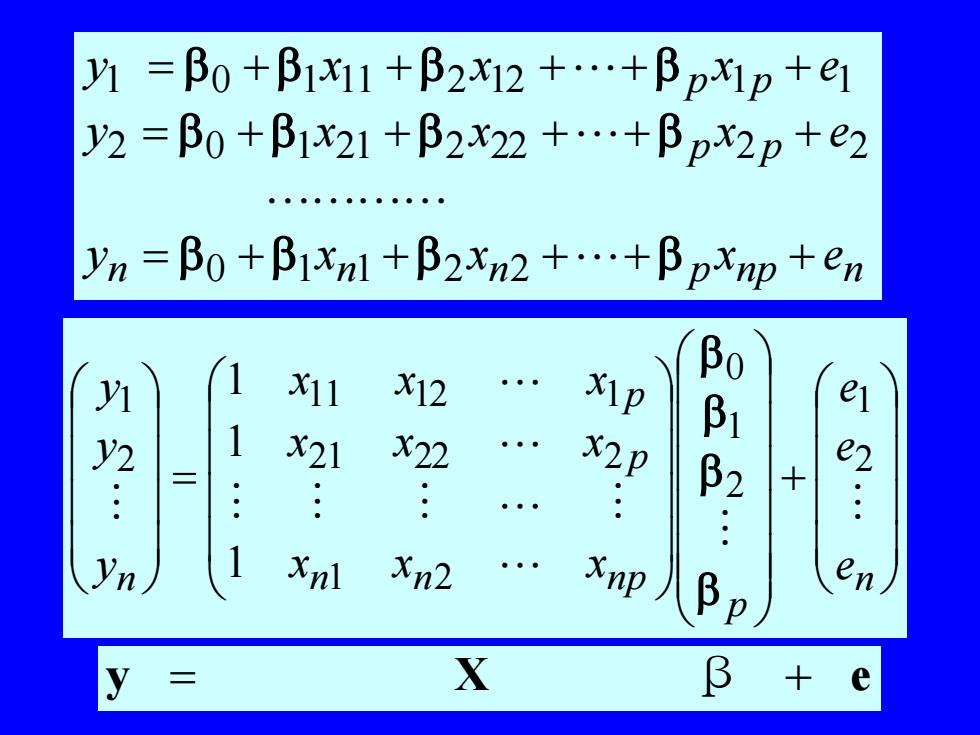
J1 =βo +βiX11 +β2X12 +...+βpX1p +eiy2 =βo +β1X21 +β2X22 +...+βpX2p +e2n =βo +βiXn1 +β2Xn2 +...+βpXnp +enβoX11X12X1eiy1BB1y22X21X22L十·..XnlenXn2XnpβpβX+e

n n n p n p n p p p p y x x x e y x x x e y x x x e = + + + + + = + + + + + = + + + + +                 0 1 1 2 2 2 0 1 21 2 22 2 2 1 0 1 11 2 12 1 1             +                             =             n p n n n p p p n e e e x x x x x x x x x y y y            2 1 2 1 0 1 2 21 22 2 11 12 1 2 1 1 1 1     y = X β + e