11-3 一边长为1=0.15m的立方体如图 放置,有一均匀磁场B=(6i+3j+1.5心T 通过立方体所在区域,计算 (1)通过立方体上阴影面积的磁通量; (2)通过立方体六面的总通量。 B 结束目录
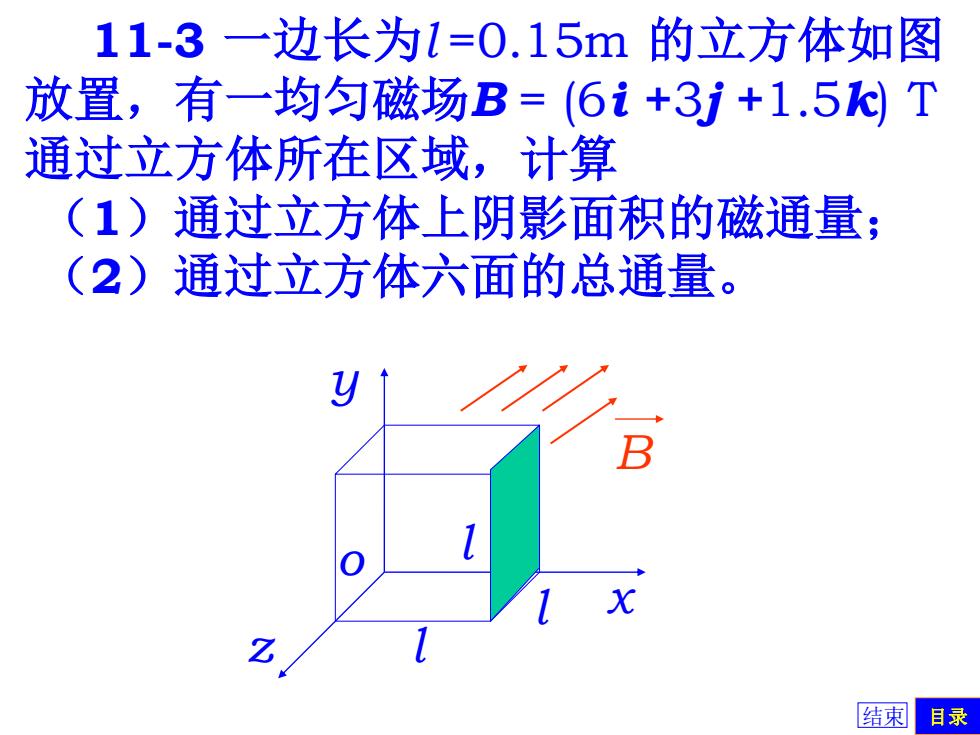
11-3 一边长为l =0.15m 的立方体如图 放置,有一均匀磁场B = (6i +3j +1.5k) T 通过立方体所在区域,计算 (1)通过立方体上阴影面积的磁通量; (2)通过立方体六面的总通量。 x y z B l o l l 结束 目录

己知:1=0.15mB=(6i+3j+1.5k)T 求:Φ 解:(1)B=(6i+3j+1.5) S=12i=0.152i Φ=B·S =(6i+3j+1.5k)-(0.152i) =0.135Wb (2)Φ'=0 结東阑 目录
= 0.135Wb 已知:l =0.15m B = ( 6i +3j +1.5k ) T Φ = B. S 解:(1) B = ( 6i +3j +1.5k ) 2 = 0.15 i 2 S = l i =( 6i +3j +1.5k ) .( ) 2 0.15 i (2) Φ´ = 0 求:Φ x y z B l o l l 结束 目录
11-4两根长直导线互相平行地放置在 真空中,如图所示,其中通以同向的电流 I1=2=10A。试求:P点的磁感应强度。 己知PI1=P2=0.5m,PI1垂直于P 2 ⊙ 结東目录
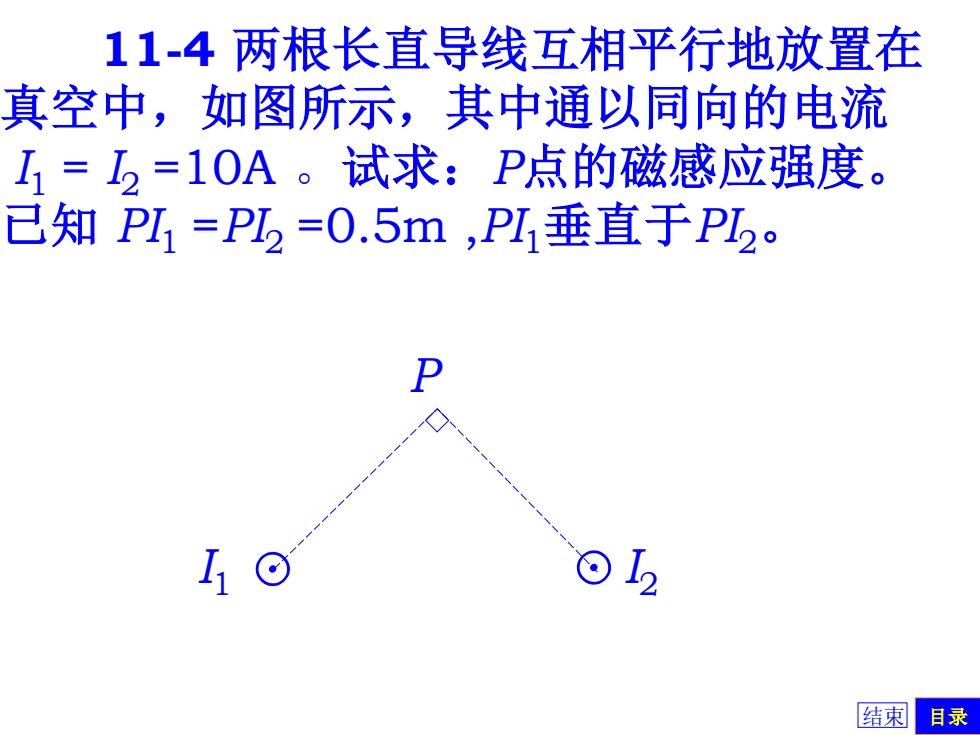
11-4 两根长直导线互相平行地放置在 真空中,如图所示,其中通以同向的电流 I1 = I2 =10A 。试求:P点的磁感应强度。 已知 PI1 =PI2 =0.5m ,PI1垂直于PI2。 I1 I2 P 结束 目录

已知:1=I2=10A PI1⊥PI2a=0.5m 求:B。 B2P 解: Bp BIP=B2P= 4o1 2元a Bp=NBip+B3p =2BIP N2×4×107×10 =5.66×106T 2元×0.50 0 arc tg B22=45° BiP 结東阑 目录
解: B1P =B2P 求:BP = m 2π 0 a 1 I BP = B1P +B2P 2 2 = 2B1P 10 = × 2×4π×10-7× 2π 0.50 = 5.66×10-6 T q = arc tg = B1P B2P 45 0 已知:I1 = I2 =10A PI1 PI2 a = 0.5m I1 I2 P a a B2P B2P BP 结束 目录
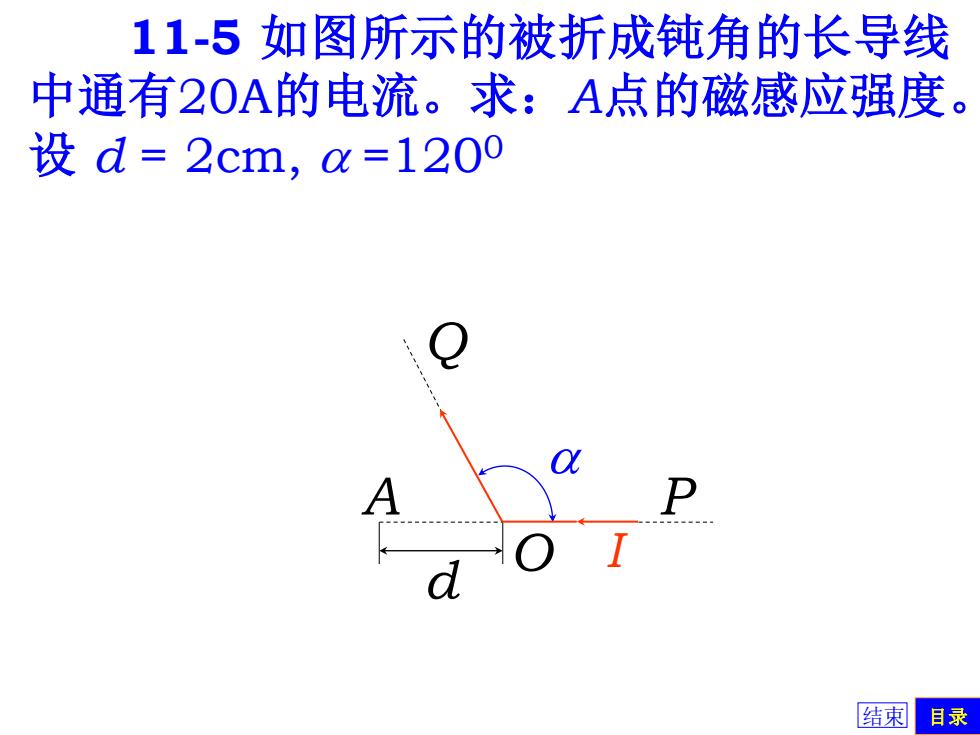
11-5如图所示的被折成钝角的长导线 中通有20A的电流。求:A点的磁感应强度。 设d=2cm,a=1200 结東目录
11-5 如图所示的被折成钝角的长导线 中通有20A的电流。求:A点的磁感应强度。 设 d = 2cm, a =1200 A P O d Q a I 结束 目录