
第三节晶体二极管电路 的分析方法
第三节 晶体二极管电路 ————的分析方法

1.3.1晶体二极管模型 在分析电路时,电路中的各个实际器件,都必须用相应的 模型来表示。力求采用最简单的模型,使电路分析简化,便 于从分析结果中直观地揭示电路的主要特性。 实际器件的模型,可以用各种形式构成: (1)、用数学表达式构成的数学模型; (2)、用曲线和表格形式构成的曲线和表格模型; (3)、用理想电路元件构成的电路模型: (4)、还可以用多种形式构成的混合模型;
1.3.1 晶体二极管模型 在分析电路时,电路中的各个实际器件,都必须用相应的 模型来表示。力求采用最简单的模型,使电路分析简化,便 于从分析结果中直观地揭示电路的主要特性。 实际器件的模型,可以用各种形式构成: (1)、用数学表达式构成的数学模型; (2)、用曲线和表格形式构成的曲线和表格模型; (3)、用理想电路元件构成的电路模型; (4)、还可以用多种形式构成的混合模型;

一、晶体二极管电路的数学模型: 在理想相条件下,推导出的数学表达式: ID =Is(e 此表达示称为晶体二极管的理想指数模型。 如果,为了反映实际器件的伏安特性,通常的做法是 将上式加以修正。 V-Irs I=Is(e nx-1) 或 =irs +nvr In(+
一、晶体二极管电路的数学模型: 在理想相条件下,推导出的数学表达式: = ( −1) VT V I D I S e 此表达示称为晶体二极管的理想指数模型。 如果,为了反映实际器件的伏安特性,通常的做法是 将上式加以修正。 = ( −1) − T S n V V Ir I I S e 或 ln(1 ) S S T I I V = Ir + nV +

V-Irs I=Is(e nv, -1) 式中n称为非理想化因子,其值与I有关。 当I为正常值时,n≈1。 当过小或过大,n≈2。 [s是与PN结相串联的电阻。(中性区的体电阻、接触 电阻、金属引线电阻) 如果,进一步考虑击穿特性和非线性电容特性,那么, 模型将会变得更为复杂
= ( −1) − T S n V V Ir I I S e 式中 n 称为非理想化因子,其值与I有关。 当I为正常值时,n ≈ 1 。 当I过小或过大, n ≈ 2 。 r S 是与PN结相串联的电阻。(中性区的体电阻、接触 电阻、金属引线电阻) 如果,进一步考虑击穿特性和非线性电容特性,那么, 模型将会变得更为复杂
二、伏安特性曲线(曲线和表格模型): 可以通过数学表达式描绘或通过实际测得到
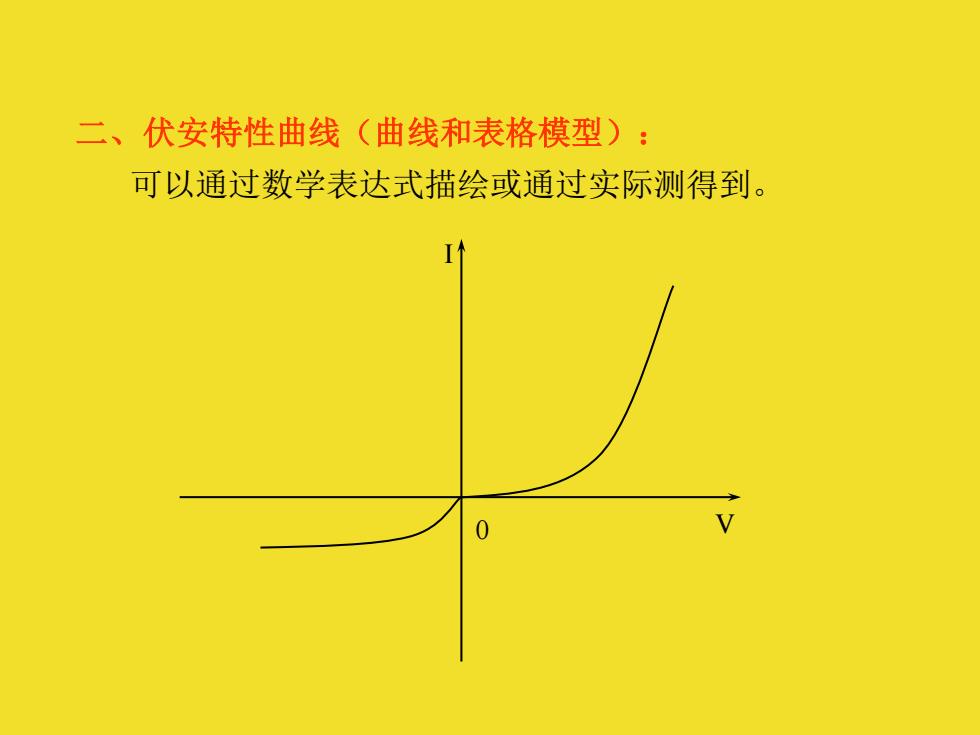
二、伏安特性曲线(曲线和表格模型): 可以通过数学表达式描绘或通过实际测得到。 0 I V