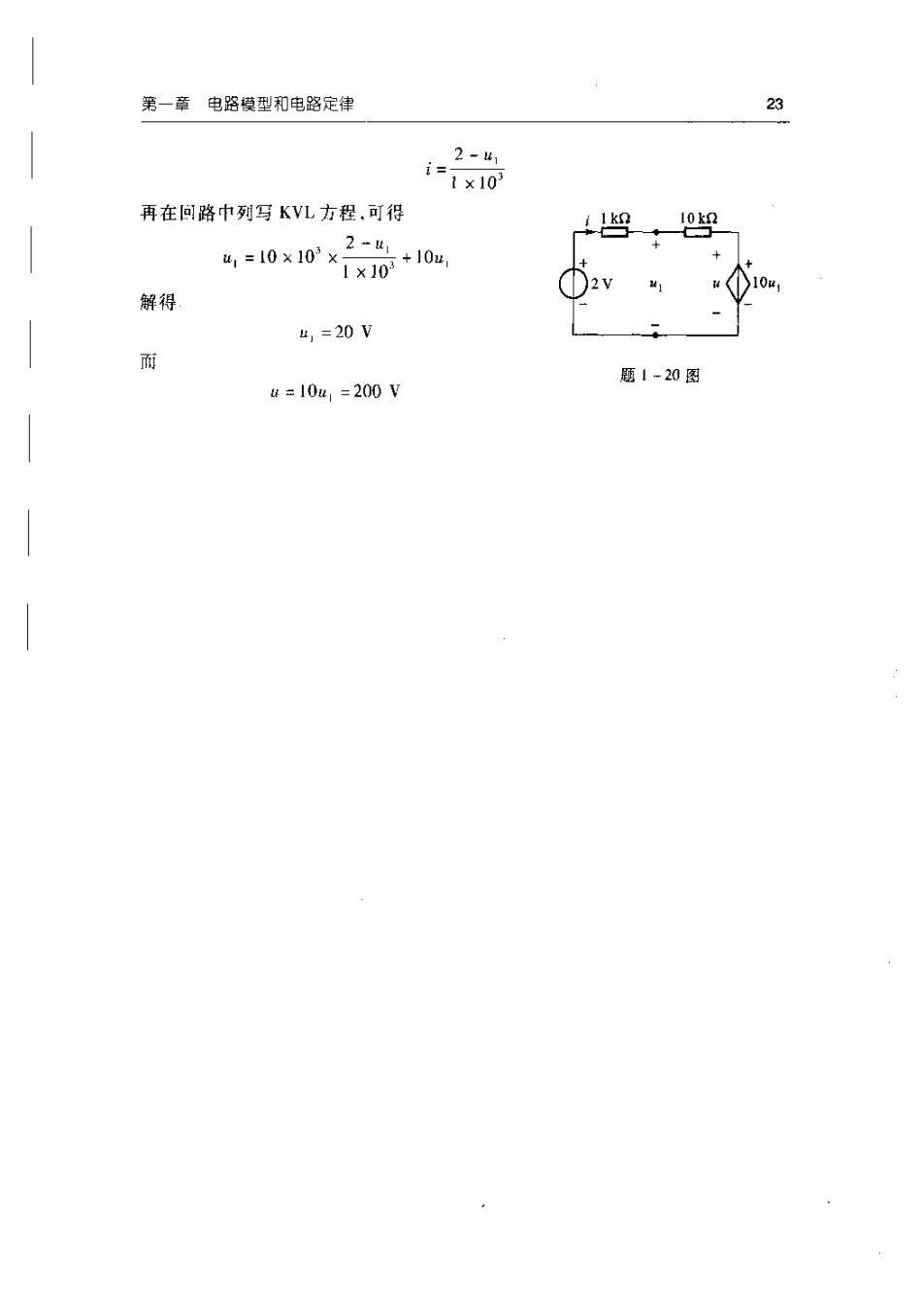
23第一章电路模型和电路定律2-ul1:1×103再在回路中列写KVL方程.可得10k2 -uu,=10×10°×+10u1 ×10解得u, =20 V而题1=20图u=10u,=200V

第二章电阻电路的等效变换一、重点和难点1.电路等效变换的概念电路等效变换的概念在电路理论中非常重要。电路等效变换的方法是电路分析中经常使用的方法,运用等效变换可以将复杂的电路化简为单回路或双结点的电路,因此,深刻理解等效变换的概念和熟练运用等效变换的方法化简电路是本章的重点。其中正确认识等效变换的条件和等效变换的目的是难点。2.电阻的串联、并联和串并联电阻的申联、并联和串并联是电阻之间主要的连接方式,一个由电阻组成的无源一端口网络,总是可以用一个等效电阻来等效替换,从而可简化电路的分析和计算,因此,熟练判别电阻的串联、并联和串并联并能运用电阻网络等效变换的方法化简电路是本章的重点。其中,判别电路中电阻的串并联关系是进行电阻网络等效变换的难点。3.实际电源的两种模型及其等效变换实际电压源的模型是理想电压源与电阻的串联组合,实际电流源的模型是理想电流源与电阻(电导)的并联组合。实际电源两种模型可以等效变换,应用实际电源两种模型的等效变换方法来化简电路也是本章的重点(注意这种等效是对外电性能等效)。受控电压源、电阻的串联组合和受控电流源、电阻(电导)的并联组合可以采用实际电源两种模型的等效变换方法来进行变换,此时,应把受控源当作独立源处理,但是注意在变换的过程中控制量必须保持完整而不被改变。在此,受控电压源、电阻的串联组合和受控电流源、电阻(电导)的并联组合之间的等效变换是电源等效变换中的难点

25第二章电阻电路的等效变换4.无源·端口网络的输入电阻无源一端口网络的输人电阻定义为此一端口的端电压与端电流之比值。理解输入电阻和等效电阻的关系,熟练掌握求解输入电阻的方法是本章重点。含受控源的一端口电阻网络输入电阻的求解是学习中的难点。二、学习方法指导1.电路等效变换的概念任何一个复杂的电路,向外引出两个端子,且从一个端子流人的电流等于从另一端子流出的电流,则称此电路为二端电路(或一端口电路)。若二端电路仅由无源元件组成,则称无源二端电路。若二端电路仅由电阻元件组成,则称纯电阻二端电路。结构和参数完全不相同的两个二端电路N,与N,,如图2-1(a)和(b)所示,当它们的端口具有相尚的电压、电流关系(VCR)时,称N,与N,是等效的电路。M++N,N21外电路u外电路1(a)(b)图2-1电路的等效变换电路等效变换的目的是化简电路,方便计算。进行等效变换时,注意电路等效变换的条件是两个电路对外具有相同的VCR,即“对外等效”的概念,也就是对外部特性等效,而两个电路的内部则是不同的。2.电阻的等效变换(1)电阻的电联串联电阻的等效电阻为各个串联电阻之和,且等效电阻大于任一个串联电阻。各个电阻上的电压值与电阻值成正比,电阻值大的分得的电压大,所以串联电阻电路可以用作分压电路。各电阻消耗(吸收)的功率与其电阻值成正比;等效电阻消耗(吸收)的功率

26(电路》(第5版)学习指导与习题分析等于各电阻消耗(吸收)的功率之和。(2)电阻的并联并联电阻的等效电阻的倒数等于各个并联电阻倒数之和,等效电阻小于任一个并联电阻。并联电导的等效电导为各个并联电导之和,且等效电导大于任一个并联电导。最常用的两个电阻并联时求等效电阻的公式如下:R,R2R.=R,+R2各并联电阻上的电流与它们各自的电导值成正比,电导值大者分得的电流大。因此,并联电阻电路可作分流电路各电阻消耗(吸收)的功率与其电导值成正比;等效电阻消耗(吸收)的功率等于各电阻消耗(吸收)的功率之和。(3)电阻的串并联电阻的串联和并联相结合的连接方式称为电阻的串并联,也称电阻的混联。(4)电阻的Y形联结和△形联结的等效变换Y-△电路的等效变换属于多端子电路的等效,在应用中,除了正确使用电阻变换公式计算各电阻值外,还必须正确连接各对应端子。其公式的简记方法为A形相邻电阻乘积 和 C. =Y 形相邻患导乘积R,=4ERZG.若三个电阻相等(对称),则有R=3Rx3.电源的等效变换(1)电压源的等效变换1)电压源的申联n个电压源串联,可以用一个等效电压源来替代,等效电压源的电压等于各个申联电压源电压的代数和。2)电压源的并联只有当电压源的电压相等且电压极性一致时,电压源才能并联。3)电压源与任意元件的并联电压源与任意元件的并联对外可等效为此电压源,如图2-2(a)所示为电压源和任意元件的并联,其等效电路如图2-2(b)所示。(2)电流源的等效变换

27第二章电阻电路的等效变换o+任意lus元件(a)(b)图2-2电压源与任意元件的并联及其等效电路1)电流源的申联只有当电流源的电流相等且电流方向一致时,电流源才能串联。2)电流源的并联n个电流源并联,可以用一个电流源等效替代,等效电流源的电流等于各个并联电流源电流的代数和。3)电流源与任意元件的串联电流源与任意元件的串联对外可等效为此电流源,如图2-3(a)所示为电流源和任意元件的串联,其等效电路如图2-3(b)所示。任意元件.(a)(b)图2-3电流源与任意元件的串联及其等效电路(3)实际电源的两种模型及其等效变换实际电源的电路模型可以是理想电压源与电阻的串联组合或者是理想电流源与电阻(电导)的并联组合,如图2-4(a)和(b)所示。实际电源两种模型可以等效变换,等效变换的条件为us1和G,=RsR.或者us=igRs禾和Rs=Gs