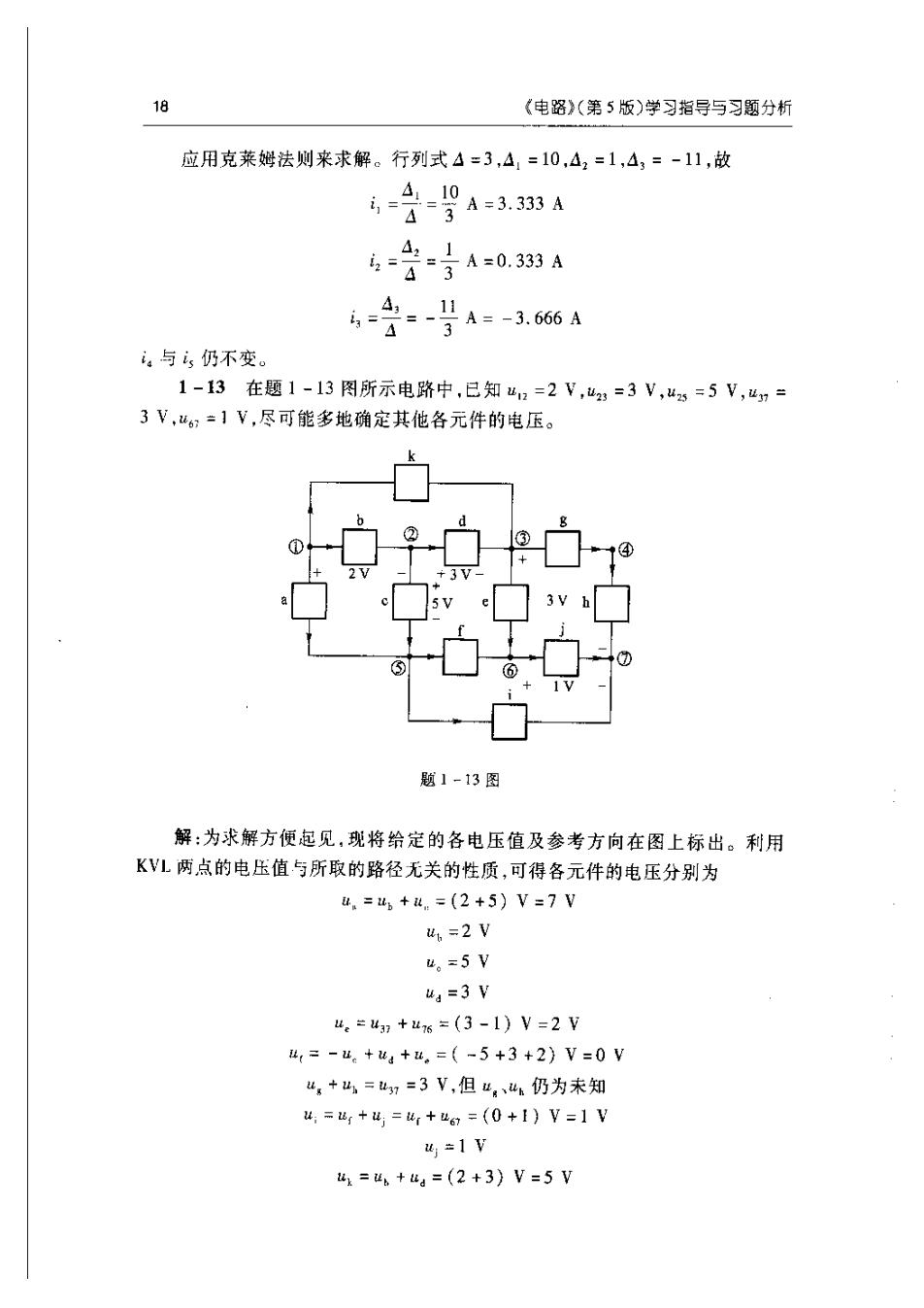
18《电路》(第5版)学习指导与习题分析应用克莱姆法则来求解。行列式4=3,4,=10,4,=1,4,=-11故A._10A=3.333 Ai, =43421A=0.333A12=434,-11A=-3.666Ai=43i与仍不变。1-13在题1-13图所示电路中,已知uiz=2V,u23=3V,u25=5V,y=3V,ug=1V,尽可能多地确定其他各元件的电压。k②3)0423VSL7?61V题1-13图解:为求解方便起见,现将给定的各电压值及参考方向在图上标出。利用KVL两点的电压值与所取的路径无关的性质,可得各元件的电压分别为u,=u,+u,=(2+5)V=7Vu, =2 Vu=5Vug=3 Vu,=ua+us=(3-1)V=2Vu,=-u+u+u,=(-5+3+2)V=0Vu,+ui==3V,但uun仍为未知u =u, +u=ur +w =(0+1)V=1 Vuj =1 Vu=u +ug=(2+3) V=5V
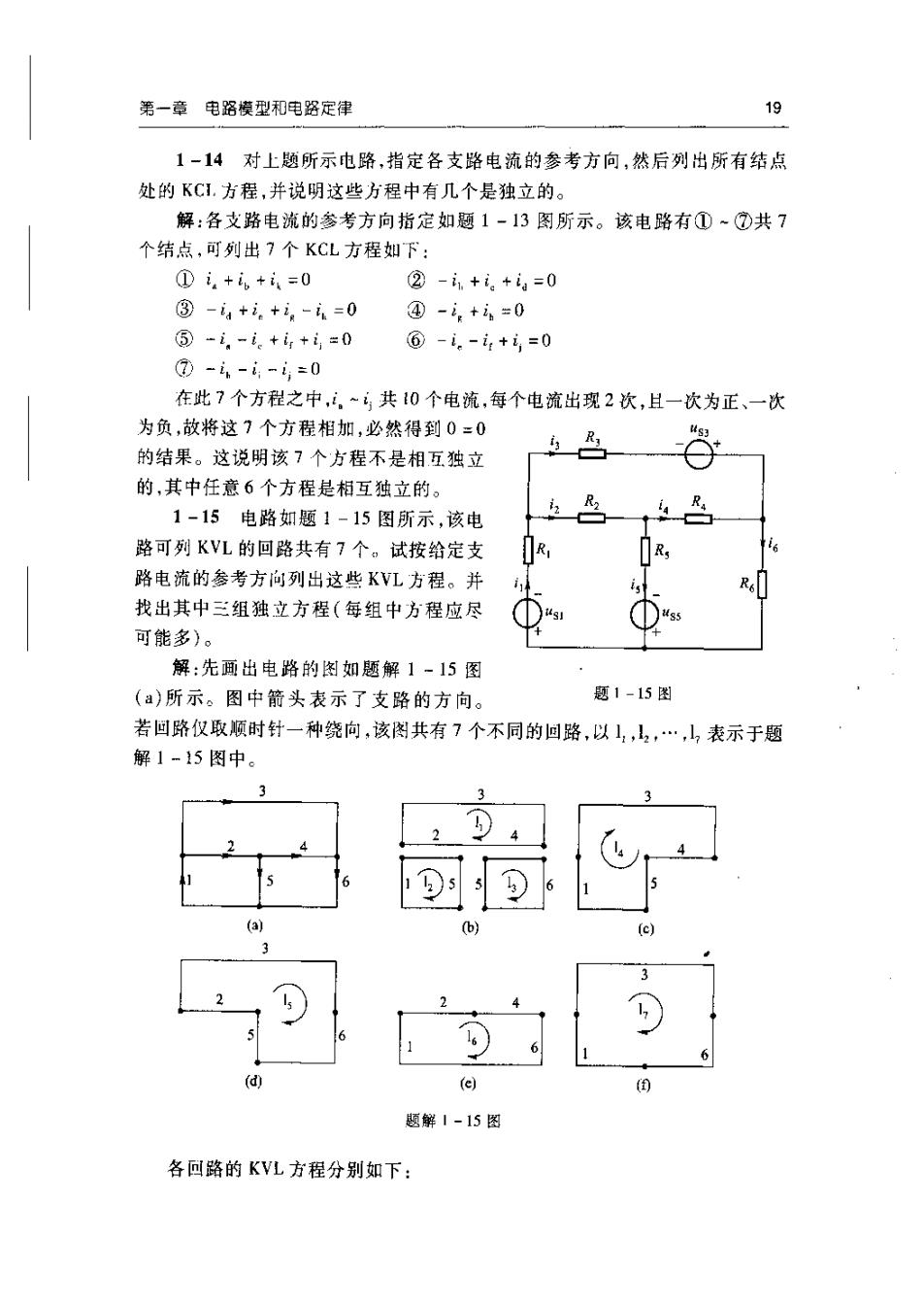
19第一章电路模型和电路定律1-14对上题所示电路,指定各支路电流的参考方向,然后列出所有结点处的KCI.方程,并说明这些方程中有几个是独立的。解:各支路电流的参考方向指定如题1-13图所示。该电路有①~①共7个结点,可列出7个KCL方程如下;Di+i+i=0② -i+i+i=0③-a+i+i-i=0①-iti=0?-i-i+i+i0@-i-i+i=0@ --t-i=0在此7个方程之中,,~;共10个电流,每个电流出现2次,且一次为正、一次为负,故将这7个方程相加,必然得到0=0s3R,i3的结果。这说明该7个方程不是相互独立的,其中任意6个方程是相互独立的。RR4it.1-15电路如题1-15图所示,该电路可列KVL的回路共有7个,试按给定支RR,路电流的参考方向列出这些KVL方程。并R找出其中三组独立方程(每组中方程应尽可能多)。解:先面出电路的图如题解1-15图题1 -15 图(a)所示。图中箭头表示了支路的方向。若回路仅取顺时针一种绕向,该图共有7个不同的回路,以1,,12,,山,表示于题解1=15图中。(a)(b)(c)(d)(e)()题解1-15图各回路的KVL方程分别如下:

20《电路》(第5版)学习指导与习题分析:Ryi,-usa -Ri,-Riz =0I,:Rzi, +R,is-uss +us, +R,i=0ly: Ris +Reis +us-Ris=0la:R,ig -ws -R,ix +R,ig -us +ugi +R,i,=0ls:Rig-us +Reig+uss-Rsis-R,iz=0I: R,i, +Ri +Reig +us +R,i, =0I,:Ryig-us +Reig +usi +R,i =0这些KVL方程不都是独立的,从方程中可看出,具有如下关系:1。=l,+1,14=1+1,1s=1,+1,以及1,=1,+1,+13。从题解1-15图也可得到此结果,例如1,和1,两个回路相加时,其中支路5就会抵消,面形成回路16,等等。因此7个回路中仅3个回路构成独立回路组。例如1,12,,;,1,,1;12,,。等都分别构成独立回路组。电路中,独立回路的数目由公式1=b-n+1决定,本题中,支路数b=6结点数n=4,故独立回路数1=6-4+1=3。1-16电路如题1-16图所示,试求每个元件发出或吸收的功率。解:(1)题1-16图(a)中,应用KVL可得到方程-U+2×0.5+2U=0解得U=-1V电流源电压U与激励电流方向非关联,因此电流源发出功率为P度=U×0.5=(-1)×0.5W=-0.5W(实际吸收0.5W)电阻功率为P,=0.52×2W±0.5WVCVS两端电压2U与流人电流方向关联,故吸收功率为Pu啦=2U×0.5=-1W(实际发出1W)显然,Pi=Puig+Pr(2)题1-16图(b)中,在结点A应用KCL,可得202020.5A12(a)(b)题1-16图

21第一章电路模型和电路定律1, = 1, +21, =31,再在左侧回路应用KVL,可得到21, +31, =2解得I =0.4A根据各电压电流方向的关联关系,可知,电压源发出功率为Pu岁 =21, =0.8 WCCCS发出功率为Pcs岁=3l,×2l,=3×0.4×2×0.4W=0.96W2Q电阻消耗功率为Pr =f, ×2 =0. 32 W10电阻消耗功率为PRz =(31,)*×1 =1.44 W显然Pus发+Pcs发=PR,+PR21-17利用KCL与KVL求题1-17图中I(提示:利用KVL将180V电源支路电流用1来表示,然后在结点①写KCL方程求解)。解:由KVL可得①2002151=20/,+180故152180, = 15/ - 1802At20在结点①列写KCL方程,有题1-17图2 +/+ 15/+1802=020可解得I=4A本题是一个双电源电路,要用KCL、KVL方程联立求解。本题中采用的方法是将列方程的过程与消去变量的过程相结合,使得解题过程较为简捷。这是一种很有用的解题技巧。1-18(1已知题1-18图(a)中,R=20,t,=1A求电流t;(2)已知题1-18图(b)中,us=10 V,i, =2A,R,=4.50,R, =10,求记。解:(1)在题1-18图(a)右方回路中,应用KVL,可得到-10-5i, +Ri=0即
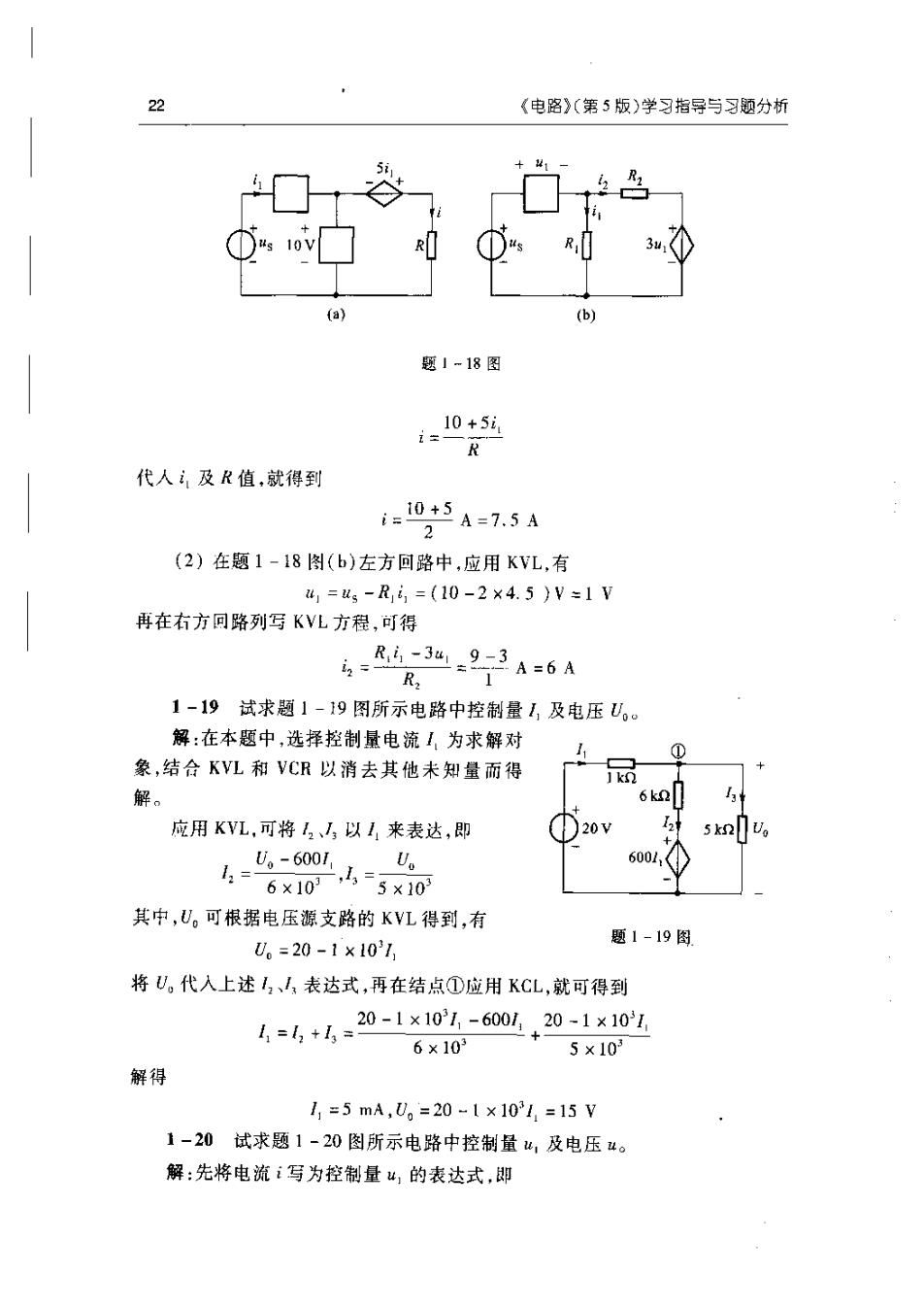
22《电路》(第5版)学习指导与习题分析TRI(a)(b)题1~18图10+5i,R代人及R值,就得到i=10 +5A=7.5A2(2)在题1-18图(b)左方回路中,应用KVL,有uj =us-Ri, =(10-2×4.5)V=1 V再在右方回路列写KVL方程,可得Ri-3ul_9-3i2=A=6AR,11-19试求题1-19图所示电路中控制量1及电压U。。解:在本题中,选择控制量电流I,为求解对11象,结合KVL和VCR以消去其他未知量而得1k解。6k应用KVL,可将、以1来表达,即U.U。-6001,60011=-5×106 ×10其中,U。可根据电压源支路的KVL得到,有题1 -19图U。 =20 -1 ×10'1将U。代入上述1,、,表达式,再在结点①应用KCL,就可得到20-1×10,-6001,201×1011 =, +I6 ×1035 ×10°解得I, =5 mA,U,=20 -1 ×10'1, =15 V1-20试求题1-20图所示电路中控制量u,及电压u。解:先将电流i写为控制量u,的表达式,即