
第一意电路模型和电路定律13题1-7图(d)中,U=-12-2I=-16V。(2)将电压方程两端均乘以1.就可得到功率方程。题1-7图(a)中功率方程为UI=121+2F,根据电压、电流方向的关联关系,UI为支路的吸收功率P支暖,121为电压源吸收的功率Pus吸,2F"为电阻吸收的功率PR。功率平衡关系为P支哦=Pus暖+Pr。这是一条用电支路:支路吸收32W,电压源吸收24W,电阻消耗8W。题1-7图(b)中功率方程为UI=121-2F。其中UI为支路发出功率,即P支发=UI=16W,12I为电压源发出功率,即Pes发=121=24W,P.为电阻消耗功率,PR=21=8W,现P发=Pus发-P#。这是一条放电支路。题1-7图(c)中功率方程为UI=-12I+2F。就功率表达式来说,UI是支路吸收功率P支吸,121为电压源发出功率Pus发,21为电阻消耗功率PR,功率平衡方程为P支=PP岁,电阻消耗功率一部分来自支路外,另一部分由支路中的电压源供给。这还应是一条用电支路。但是现在U<0,P支坚<0,考虑到P变吸=P支发,故上式应改为P支爱=Pns发-Pr,这与放电支路(b)的情况相同。题1-7图(d)中功率方程为UI=-2P-12I,意味着P支发=-P-Pu吸。从此代数式可看出:P支发、P,与Pus吸三者不可能同时为正,其中至少有一项功率为负(三项功率也不可能同时为负)。现在由于U<0,因此,P支发<0,上式可改写为P支要=Pus吸+P,这和图(a)的情况相同。支路的功率情况,仅为三种,第一种:支路吸收,电源吸收;第二种,支路发出,电源发出;第三种:支路吸收,电源发出。电阻总为耗能。1-8试求题1-8图中各电路的电压U,并分别讨论其功率平衡。解:图中各电路从电阻两端求支路电压。(1)题1-8图(a中,U=2×(2+6)V=16V。U、I方向关联、支路吸收功率P暖=UI=16×2W=32W;电流源两端电压与激励电流非关联,电流源发162出功率Pix=16×6W=96W;电阻功率P=号W=128W。可见P支吸=Pk-UPis发。功率方程也可从电流方程1=号-6两端乘以U后得到。2(2)题1-8图(b)中,U=(6-2)×2V=8V。P支度=UI=8×2W=16W,8°电流源发出功率Pl发=U×6=8×6W=48W,电阻功率P,W=32W。功=2率平衡为P支发=P发-PR。(3)题1-8图(c)中,U=(2-4)×3V==6V。支路吸收功率P支吸=UI=(-6)×2W=-12W,电流源吸收功率P发=U×4=-24W,电阻功率
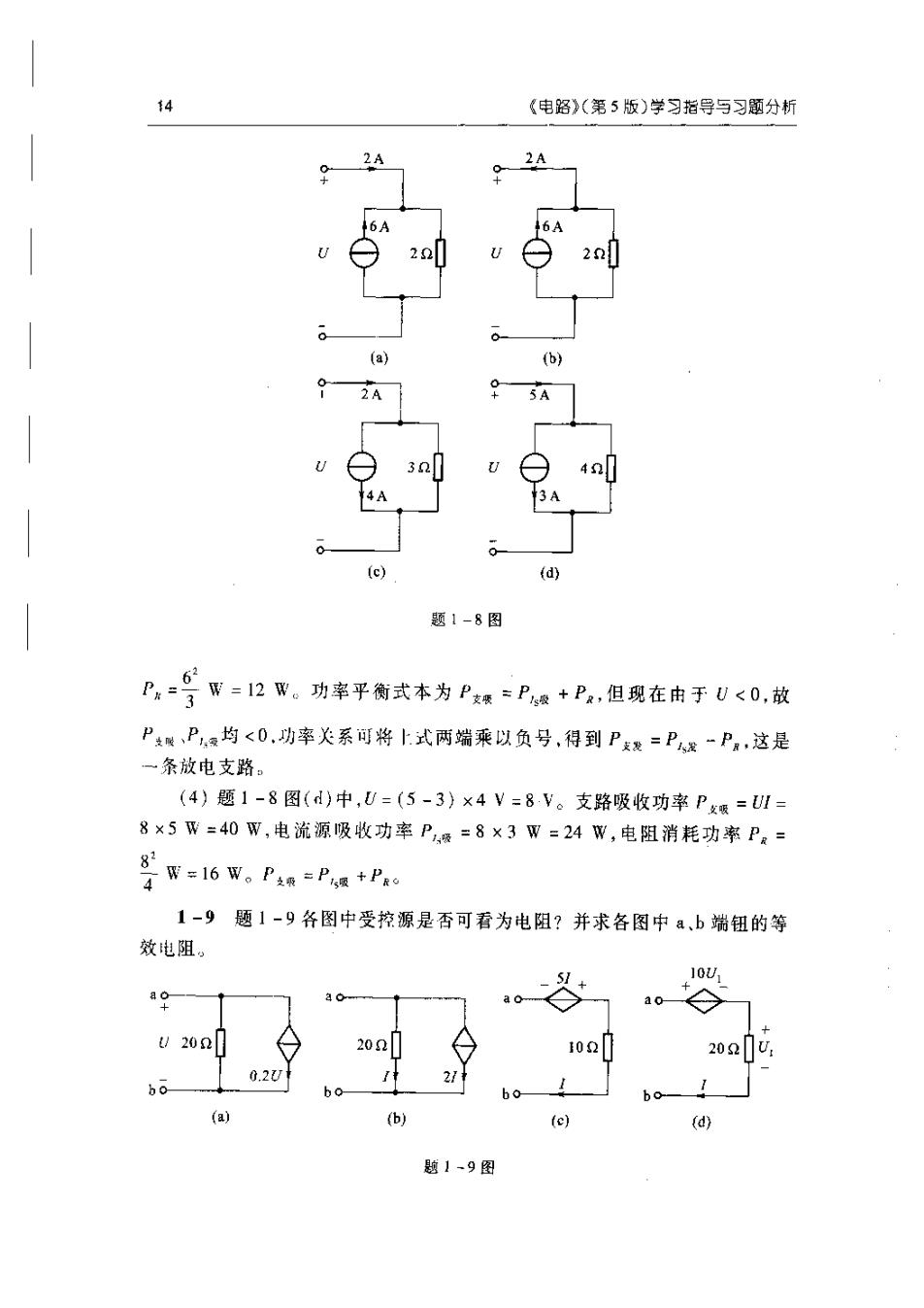
14《电路》(第5版)学习指导与习题分析2A2A6A20(a)(b)2.A5A04A3A(c)(d)题1-8图62PrW=12W。功率平衡式本为P支顺=Pi+PR,但现在由于U<0,故W3P麦度、P,均<0.功率关系可将上式两端乘以负号,得到Px=Pi一P,这是一条放电支路。(4)题1-8图(d)中U=(5-3)×4V=8V。支路吸收功率P文暖=UI=8×5W=40W,电流源吸收功率P吸=8×3W=24W,电阻消耗功率P=82W=16W。P±*=Ps+PRo41-9题1-9各图中受控源是否可看为电阻?并求各图中a、b端钮的等效电阻:CU2022022090.20121boho(a)(b)(c)(d)题1-9图

15第一章电路模型和电路定律解:如果一个受控源可求得其两端的电压与受控源的电流成正比,该受控源就可看为一个电阻,其阻值为受控源上电压与关联方向电流的比值。如果这个比值是一个正数,受控源就相当于二个正电阻;如果比值是负数,受控源就相当于一个负电阻。(1)题1-9图(a)中,受控源中的电流Ics=0.2U;U为受控源两端的电压,方向与电流方向关联。受控源相当于电阻URes=0.20=50而20 ×5Rab =0=4020+5(2)题1-9图(b)中,受控源两端电压为U,电流2与U方向关联,故U_201Res21=21=10010×20而Ra=10+20Q=6.667(3)题1-9图(c)中,受控电压源的电压为51.但与电压源中的电流方向非关联,因此CCVS相当于电阻51R..-50而R=10+R=(10-5)0=50(4)题1-9图(d)中,受控源两端电压为10U,其中的电流I方向与之关U.10U,10U,联,且有1=,因此,受控源相当于电阻R=2002201U/20而R=(200+20)0=220Q以上各题中求R,时,也可直接从U与输人电流的比值一次求出R。另一方面,也可通过观察来求出受控源相当的电阻。例如在题1-9图(b)中,处于同样电压下,20流过的电流为1,而CCCS元件电流为其2倍,其相当的电阻是20的一半,即1001-10电路如题1-10图所示,试求:(1)图(a)中,i与u;(2)图(b)中,uebo解:(1)如题1-10图(a)所示,CCCS中的电流根据题意有100.9i, =iA=2A5
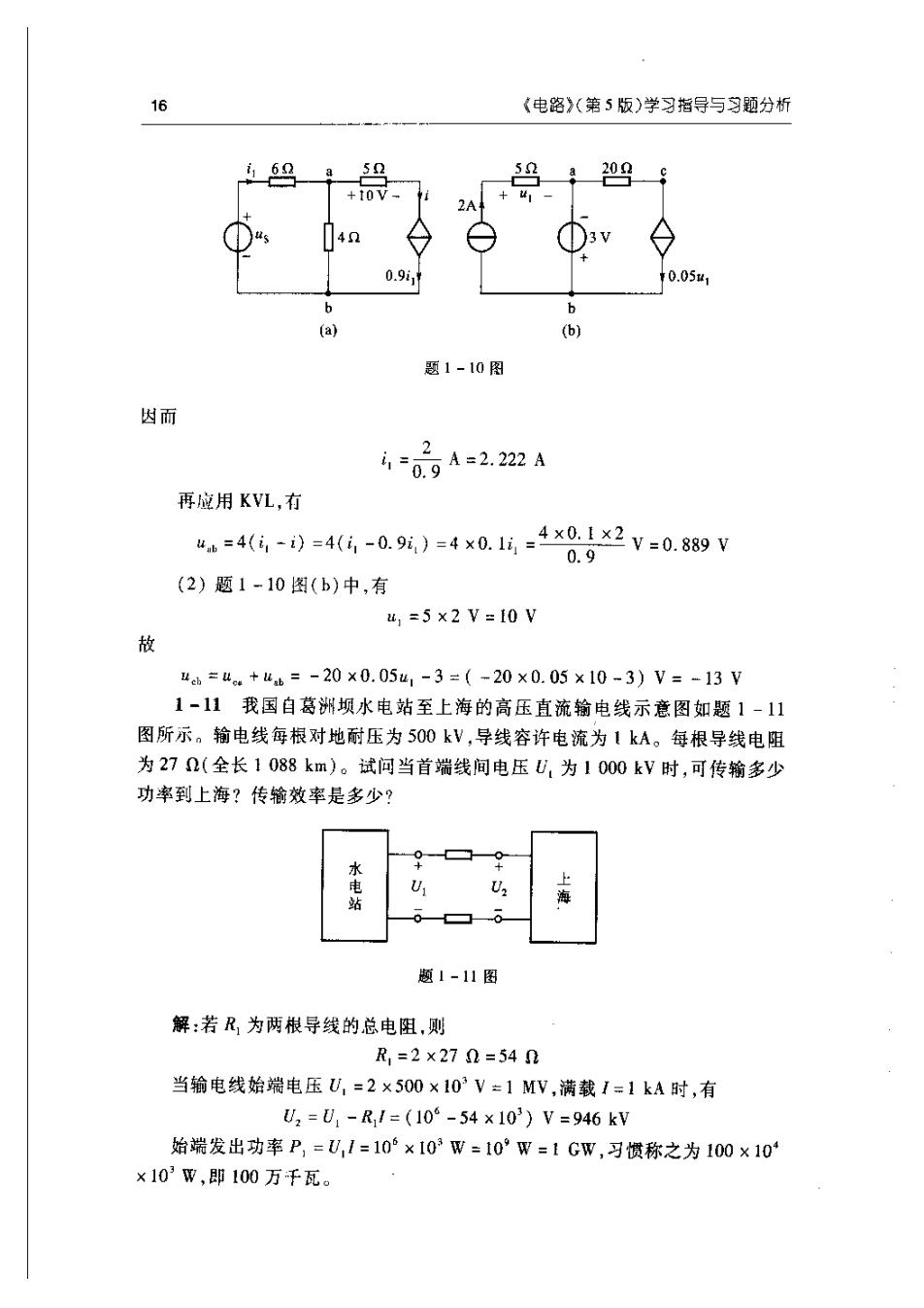
16《电路》(第5版)学习指导与习题分析000.9,0.05ubb(a)(b)题1-10图因而2A =2. 222 A0.9再应用KVL,有ua =4(i; -1i) =4(i -0. 9i.) =4 0. i, =4 0.↓ ×2 =0.889 0.9(2)题1-10图(b)中,有u, =5 ×2 V-10 V故ue=u+ua=-20×0.05u,-3=(~20×0.05×10-3)V=-13V1-11我国自葛洲坝水电站至上海的高压直流输电线示意图如题1-11图所示。输电线每根对地耐压为500kV,导线容许电流为1kA。每根导线电阻为272(全长1088km)。试问当首端线间电压U,为1000kV时,可传输多少功率到上海?传输效率是多少?水电站上UiU2海题1-11图解:若R,为两根导线的总电阻,则R,=2×27Q=540当输电线始端电压U,=2×500×10°V=1MV,满载I=1kA时,有U, =U, -R,/=(10°- 54 ×10°) V =946 kV始端发出功率P,=U,1=10°×10°W=10°W=1GW,习惯称之为100×10*×10°W,即100万千瓦

17第一章电路模型和电路定律终端接受功率P,=U1=946×10°×10°W=0.946GW,或94万6千千瓦。线路功率传输损失为△P=P-P=54MW(5万4于千瓦)传输效率为Pzn(%) :×100%=94.6%P,1-12对题1~12图所示电路,若:(1)R、Rz、R,不定;(2) R =R, =R,在以上两种情况下,尽可能多地确定各电阻中的未知电流。ZA10A/N6A题1=12图解:给定未知电流参考方向如图。(1)当R、R,、R,阻值不定时,对R,R2、R,三个电阻所构成的回路(网孔)无法列出KVL方程,因此i、i、i不定;但可根据封闭面S形成的广义结点(或超结点)写出KCL方程而得到i +6=3+4即i=(7-6)A=1A在N,结点列出KCL方程,有i, +(-10) =2+1即i,=13A(2)当R,=R,=R,时,对封闭面S所包含的电路,包含了三个结点、一个网孔,可写出两个KCL方程和一个KVL方程,它们分别为-iz=3iz-ij=4IRi, +Riz +Ri, =0