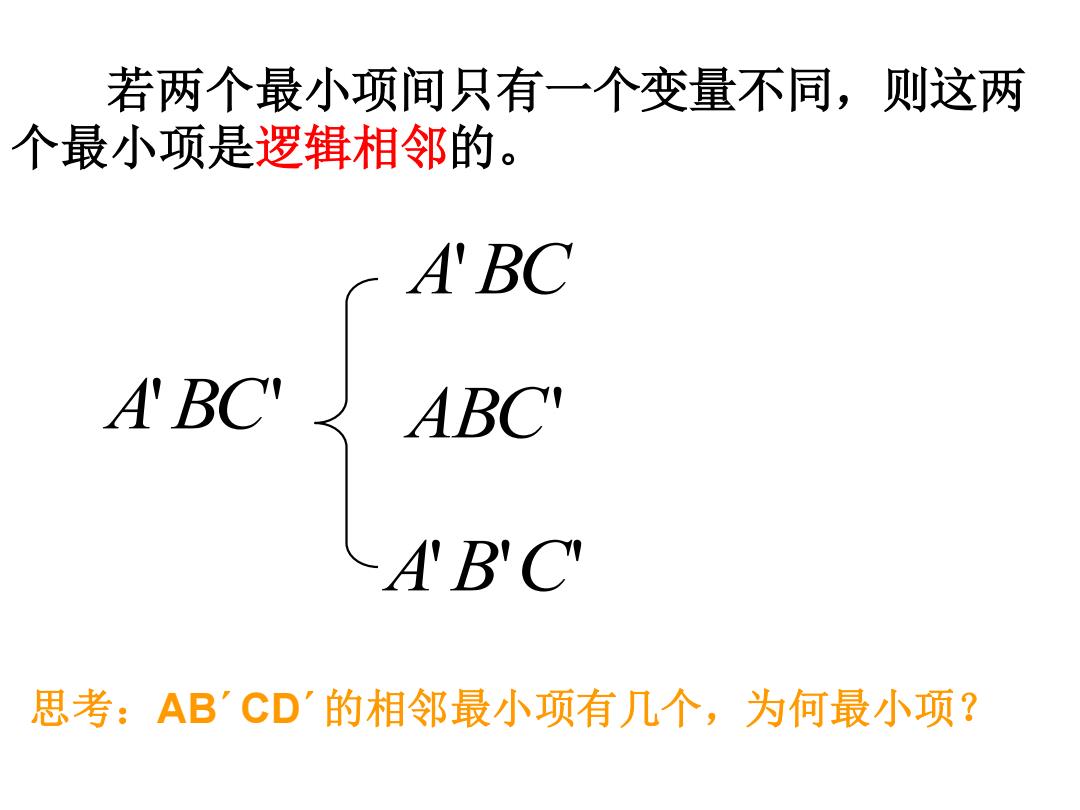
若两个最小项间只有一个变量不同,则这两 个最小项是逻辑相邻的。 ABC ABC 思考:AB'CD'的相邻最小项有几个,为何最小项?
若两个最小项间只有一个变量不同,则这两 个最小项是逻辑相邻的。 A'BC' A'BC ABC' A'B'C' 思考:AB´CD´的相邻最小项有几个,为何最小项?

2、逻辑函数式的最小项之和形式 利用基本公式A+A'=1可以把任何逻辑函数化为最小 项之和的标准形式。 例1:Y(A,B,C)=A'BC+AC'+B'C 解:Y(A,B,C)=A'BC+A(B+B)C'+(A+A')B'C =A'BC+ABC'+AB'C'+AB'C+A'B'C =m3+m6+m4+ms+m1 =2m(1,3,4,5,6)
例1:Y(A,B,C) = A´BC+AC´+B´C 解:Y(A,B,C) = A´BC+A(B+B´)C´+(A+A´)B´C = A´BC+ABC´+AB´C´+AB´C+A´B´C = m3 + m6 + m4 + m5 + m1 = m(1,3,4,5,6) 2、逻辑函数式的最小项之和形式 利用基本公式 A+A´=1 可以把任何逻辑函数化为最小 项之和的标准形式

例2:Y(A,B,C,D)=(AD+A'D'+B'D+C'D')' 解:Y(A,B,C,D)=(AD)'(A'D')'(B'D)'(C'D')' =(A'+D')A+D)(B+D')(C+D) =A'BD+ACD' =A'B(C+C)D+A(B+B)CD =A'BCD+A'BC'D+ABCD'+AB'CD =m7+m5+m14+m10 =2m(5,7,10,14)
例2:Y(A,B,C,D)=(AD+A´D´+B´D+C´D´) ´ 解:Y(A,B,C,D) = (AD) ´(A´D´) ´(B´D) ´(C´D´) ´ = (A´+D´)(A+D)(B+D´)(C+D) = A´BD+ACD´ = A´B(C+C´)D+A(B+B´)CD´ = A´BCD+A´BC´D+ABCD´+AB´CD´ = m7 + m5 + m14 + m10 = m(5,7,10,14)