
EX.2.1 Non-Periodic Sequences x2[n]=cos(n) Suppose it is periodic sequence with period N x2[n]=x2[n+N门 cos(n)=cos(n+N) forn+2πk=n+N, k:integer, there is no integer N 27 10/18/2022 Zhongguo Liu_Biomedical Engineering_Shandong Univ
27 10/18/2022 Zhongguo Liu_Biomedical Engineering_Shandong Univ. EX. 2.1 Non-Periodic Sequences ◆Suppose it is periodic sequence with period N [ ] [ ] x2 n = x2 n + N x n n 2 [ ] cos = ( ) cos( n) = cos(n+ N) 2 , : integer, integer for n k n N k there is no N + = +
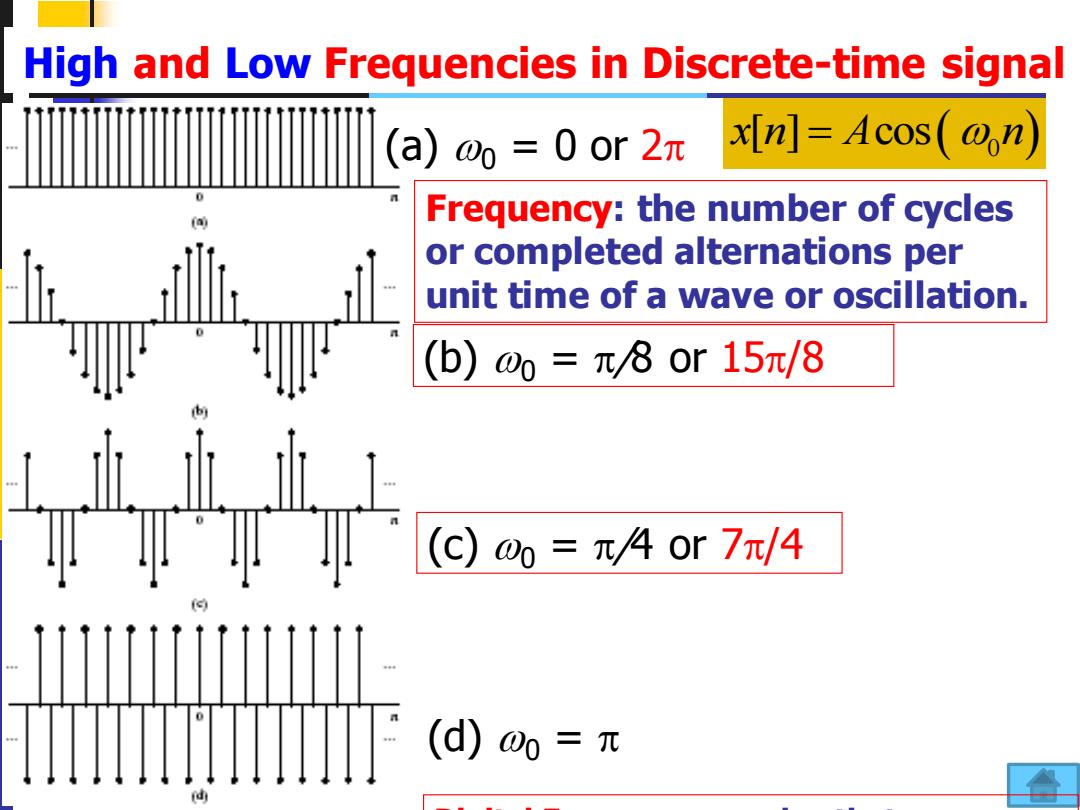
High and Low Frequencies in Discrete-time signal (a)o=0or2π xIn]=Acos(@on) Frequency:the number of cycles or completed alternations per unit time of a wave or oscillation. (b)0=元/80r15π/8 (C)=π/40r7/4 (d) 00 二元 d
28 10/18/2022 High and Low Frequencies in Discrete-time signal x n A n [ ] cos = ( 0 ) (d) 0 = Frequency: the number of cycles or completed alternations per unit time of a wave or oscillation. (a) 0 = 0 or 2 Digital Frequency: a value that expresses (b) 0 = /8 or 15/8 (c) 0 = /4 or 7/4
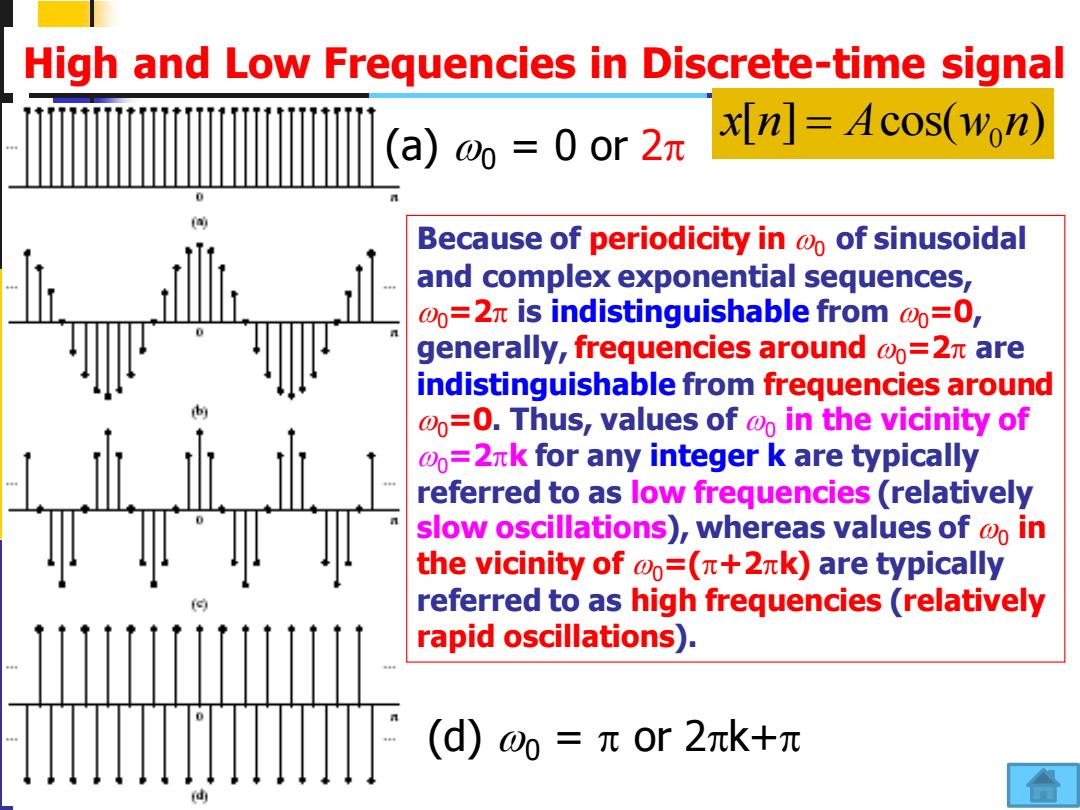
High and Low Frequencies in Discrete-time signal (a)0=0or2元 x[n]=Acos(won) 0 Because of periodicity in @o of sinusoidal and complex exponential sequences, @0=2 is indistinguishable from @0=0, generally,frequencies around @o=2n are indistinguishable from frequencies around @0=0.Thus,values of @o in the vicinity of @0=2xk for any integer k are typically referred to as low frequencies (relatively slow oscillations),whereas values of @o in the vicinity of @o=(n+2k)are typically referred to as high frequencies (relatively rapid oscillations). (d)o0=元or2πk+元
29 10/18/2022 High and Low Frequencies in Discrete-time signal 0 x n A w n [ ] cos( ) = (d) 0 = or 2k+ Because of periodicity in 0 of sinusoidal and complex exponential sequences, 0=2 is indistinguishable from 0=0, generally, frequencies around 0=2 are indistinguishable from frequencies around 0=0. Thus, values of 0 in the vicinity of 0=2k for any integer k are typically referred to as low frequencies (relatively slow oscillations), whereas values of 0 in the vicinity of 0=(+2k) are typically referred to as high frequencies (relatively rapid oscillations). (a) 0 = 0 or 2

2.2 Discrete-Time System Discrete-Time System is a trasformation or operator that maps input sequence x[n]into an output sequence y[n]. ◆y[n]=Tx[n]; x[n],y[n]:discrete-time signal x[n] T yin] Discrete-Time System 30 10/18/2022 Zhongguo Liu_Biomedical Engineering_Shandong Univ
30 10/18/2022 Zhongguo Liu_Biomedical Engineering_Shandong Univ. 2.2 Discrete-Time System ◆Discrete-Time System is a trasformation or operator that maps input sequence x[n] into an output sequence y[n]. ◆y[n]=T{x[n]}; x[n], y[n]: discrete-time signal T{‧} x[n] y[n] Discrete-Time System

EX.2.2 The Ideal Delay System y(n]=xIn-nal, -0<n<0 If n,is a positive integer:the delay of the system,Shift the input sequence to the right by nsamples to form the output If n,is a negative integer:the system will shift the input to the left byns samples, corresponding to a time advance. 31 10/18/2022 Zhongguo Liu_Biomedical Engineering_Shandong Univ
31 10/18/2022 Zhongguo Liu_Biomedical Engineering_Shandong Univ. EX. 2.2 The Ideal Delay System y[n] = x[n − nd ], − n ◆If is a positive integer: the delay of the system, Shift the input sequence to the right by samples to form the output . d n d n ◆If is a negative integer: the system will shift the input to the left by samples, corresponding to a time advance. d n d n