
12.1力的功 12.1.3常见力的功 1)重力的功 M M 设质点的质量为m,在重力 作用下从M1运动到M2。建立如 21 mg 图坐标,则 22 F=0,F=0,F=-ng 代入功的解析表达式得 W2=∫(-mg)dz=mg(,-2)
1) 重力的功 设质点的质量为m,在重力 作用下从M1运动到M2。建立如 图坐标,则 0, 0, F F F mg x y z = = = − 代入功的解析表达式得 2 1 12 1 2 ( )d ( ) z z W mg z mg z z = − = − 12.1.3 常见力的功 12.1 力的功 M1 M2 M mg z1 z2 O x y z

常见力的功 对于质点系,其重力所作的功为 W2=∑m,8(21-22) =(∑m,1-∑m,22)g =(MEcI-MEc2)g =Mg(2c1-2c2) 由此可见,重力的功仅与重心的始末位置有关,而与 重心走过的路径无关
对于质点系,其重力所作的功为 12 1 2 1 2 1 2 1 2 ( ) ( ) ( ) ( ) i i i i i i i C C C C W m g z z m z m z g Mz Mz g Mg z z = − = − = − = − 由此可见,重力的功仅与重心的始末位置有关,而与 重心走过的路径无关。 常见力的功

常见力的功 2)弹力的功 0 物体受到弹性力 的作用,作用点的轨 迹为图示曲线A1A2, 在弹簧的弹性极限内, 弹性力的大小与其变 形量6成正比。设弹 簧原长为,则弹性 力为 F=-k(r-lo)to W2=∫Fdr=∫-k(r-6)dr
2 ) 弹力的功 物体受到弹性力 的作用 , 作用点的轨 迹 为图 示曲线 A 1 A 2 , 在弹簧的弹性极限内 , 弹性力的大小与其变 形量 d 成正比 。设弹 簧原长为 l0 , 则弹性 力为 0 0 F r = − − k r l ( ) 2 2 1 1 12 0 0 d ( ) d A A A A W k r l = − − F r = r r A 1 A 2 r2 r 1 l 0 Or0r A d F A 0 d r 常见力的功

常见力的功 因为 _L.dr =2r 于是 =-6d=[G-4-4门 或 W,=号(82-) 2 弹性力作的功只与弹簧在初始和末了位置的变形量有 关,与力的作用点A的轨迹形状无关
于是 2 1 2 2 12 0 1 0 2 0 1 ( )d ( ) ( ) 2 r r W k r l r k r l r l = − − = − − − 或 ( ) 2 1 2 2 2 W12 = k d 1 −d 因为 2 0 1 1 d d d( ) d d 2 2 r r r r r = = = = r r r r r r 弹性力作的功只与弹簧在初始和末了位置的变形量有 关,与力的作用点A的轨迹形状无关。 常见力的功
常见力的功 3)定轴转动刚体上作用力的功 设作用在定轴转动则体上A点的力为F, 将该力分解为F、Fn和Fb, F=Fcose 当则体转动时,转角p与孤长5的关系为 ds Rdo R为力作用点A到轴的垂距。力F的元 功为 W=F.dr=Fds=FRdo=M.do 力F在则体从角四转到2所作的功为 m。=M.do M,可视为作用在刚体上的力偶
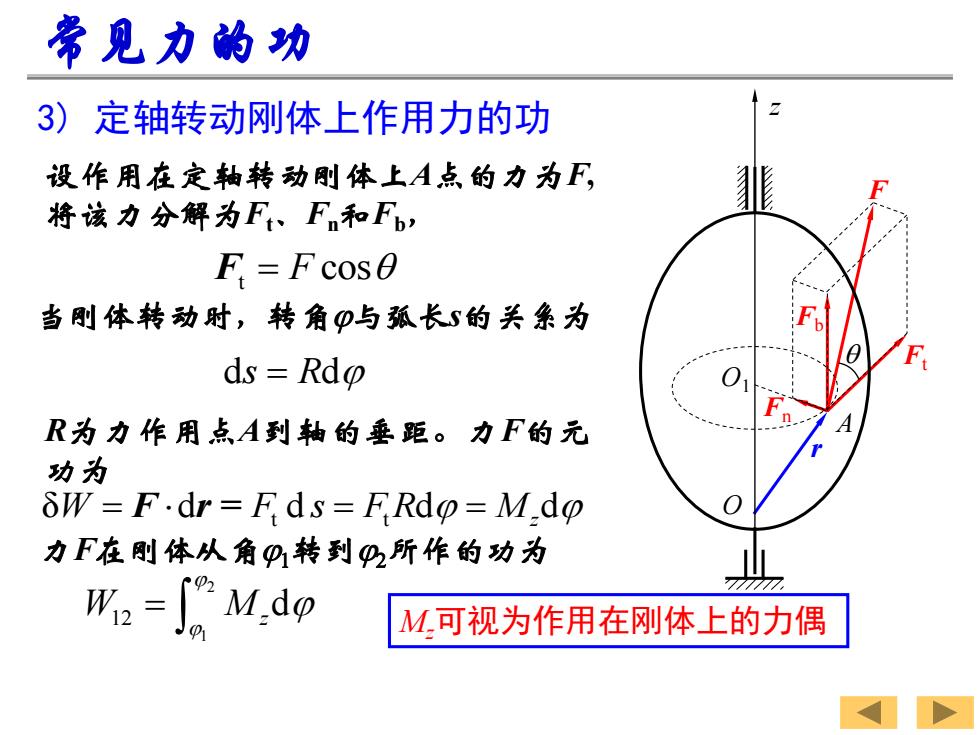
3) 定轴转动刚体上作用力的功 设作用在定轴转动刚体上A点的力为F, 将该力分解为Ft、Fn和Fb, 常见力的功 当刚体转动时,转角j与弧长s的关系为 t F = F cos d d s R = j R为力作用点A到轴的垂距。力F的元 功为 t t δ d d d d W F s F R M = = = F r = j jz Ft F r Fb Fn O z O1 A 力F在刚体从角j1转到j2所作的功为 2 1 12 d W Mz j j = j Mz可视为作用在刚体上的力偶