对数模率特性(BodB圆)】 典型环节的B0da国 典型环节的Bode图 网积分环节c0)={=0 20大Uw)dB 当c)=(白°{ L(w)=-20algw 0 (w)=-a*90° -20 (4惯性环节Gw)=中 ∫L(w)=-20lgV1+w2T ↑(w) 90 (w)=-arctanwT -90° ↑(o) ↑L(w)dB 0° -90° -20 -180° -40 第五章线性系统的过分折 自动控制膜理 电子信息学院161118
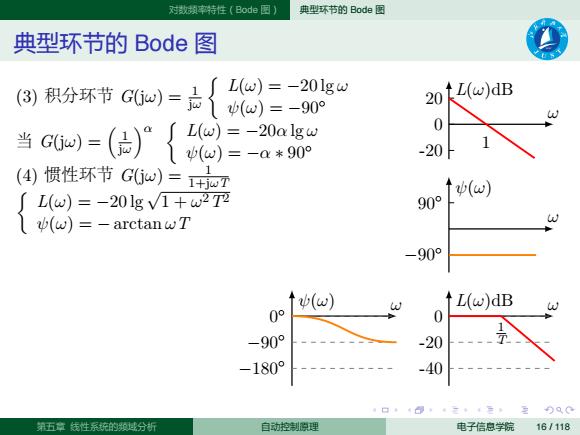
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 对数频率特性(Bode 图) 典型环节的 Bode 图 典型环节的 Bode 图 ω L(ω)dB -20 0 20 1 ω ψ(ω) −90◦ 90◦ L(ω)dB ω -40 -20 0 1 T ψ(ω) ω −180◦ −90◦ 0 ◦ (3) 积分环节 G(jω) = 1 jω { L(ω) = −20 lg ω ψ(ω) = −90◦ 当 G(jω) = ( 1 jω )α { L(ω) = −20α lg ω ψ(ω) = −α ∗ 90◦ (4) 惯性环节 G(jω) = 1 { 1+jωT L(ω) = −20 lg √ 1 + ω2T2 ψ(ω) = − arctan ωT 第五章 线性系统的频域分析 自动控制原理 电子信息学院 16 / 118

对数率特性(Bode园】 典型环节的B0de因 典型环节的Bode图 (⑤)一阶微分 40 L(w)dB G(s)=Ts+1 G(jw)=1+jwT 了L(w)=20lgV1+w2T 20 20dB/dec (w)=arctanwT 0.01 0.1 10 100 180° (w) 135° 90° 45° 0 0.01 0.1 10 100 第五章线性系统的域分析 自动控制膜理 电子信息学院171118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 对数频率特性(Bode 图) 典型环节的 Bode 图 典型环节的 Bode 图 ω 0.01 0.1 1 10 100 L(ω)dB 0 20 40 20dB/dec ω 0.01 0.1 1 10 100 ψ(ω) 0 ◦ 45◦ 90◦ 135◦ 180◦ (5) 一阶微分 G(s) = Ts + 1 G(jω) = 1 + jωT { L(ω) = 20 lg √ 1 + ω2T2 ψ(ω) = arctan ωT 第五章 线性系统的频域分析 自动控制原理 电子信息学院 17 / 118
对数湖率特推(Bode圆) 典型环节的B0da国 典型环节的Bode图 (6)震荡环节 L(w)dB 0.3 5 好 1 0 G(s)= 0.7 2+2Ewns+w + 2+1 0.85 -20 1 G(0jw)= 1- 器等+2兴 -40 L(w)=-20lg V1-+2兰卫 (w)dB (w)=arctan (2“)/(1-)] 品<1 L(w)≈0 (w)≈0 >1 L(w)≈-40lg(w/wn) (w)≈-180° -180° 里0只0 第五章线性系统的过分折 自动控制膜理 电子信息学院181118
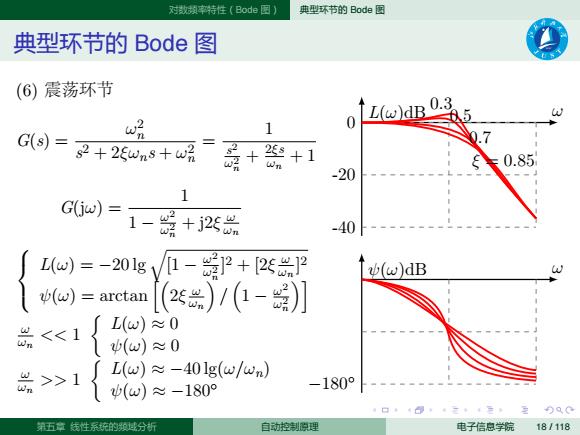
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 对数频率特性(Bode 图) 典型环节的 Bode 图 典型环节的 Bode 图 L(ω)dB ω 0 -20 -40 0.3 0.5 0.7 ξ = 0.85 ψ(ω)dB ω −180◦ (6) 震荡环节 G(s) = ω 2 n s 2 + 2ξωns + ω2 n = 1 s 2 ω2 n + 2ξs ωn + 1 G(jω) = 1 1 − ω2 ω2 n + j2ξ ω ωn L(ω) = −20 lg√ [1 − ω2 ω2 n ] 2 + [2ξ ω ωn ] 2 ψ(ω) = arctan [(2ξ ω ωn ) / ( 1 − ω 2 ω2 n )] ω ωn << 1 { L(ω) ≈ 0 ψ(ω) ≈ 0 ω ωn >> 1 { L(ω) ≈ −40 lg(ω/ωn) ψ(ω) ≈ −180◦ 第五章 线性系统的频域分析 自动控制原理 电子信息学院 18 / 118

对数率特性(Bode园】 典型环节的Bode国 典型环节的Bode图 谐振频率w,和谐振峰值M, L()-201g1G1=201g1/[ 是q-0是{-+r}-0 21--2÷1+2g兰)=0 的-1+3+29=0 Wr WnV1-282 =1-22 4,=201g1G0i=201g2G√1-e 第五章线性系统的域分析 自动控制膜理 电子信息学院 191118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 对数频率特性(Bode 图) 典型环节的 Bode 图 典型环节的 Bode 图 谐振频率 ωr 和谐振峰值 Mr L(ω) = 20 lg |G| = 20 lg 1/√ [1 − ω2 ω2 n ] 2 + [2ξ ω ωn ] 2 d dω |G| = 0 d dω { [1 − ω 2 ω2 n ] 2 + [2ξ ω ωn ] 2 } = 0 2[1 − ω 2 ω2 n ][−2( ω ωn )] + 2[2ξ ω ωn ]( 2ξ ωn ) = 0 4ω ω2 n [−1 + ω2 ω2 n + 2ξ 2 ] = 0 ω 2 ω2 n = 1 − 2ξ 2 { ωr = ωn √ 1 − 2ξ 2 Mr = 20 lg |G(jωr)| = 20 lg 1 2ξ √ 1−ξ 2 第五章 线性系统的频域分析 自动控制原理 电子信息学院 19 / 118

对数损率特性(BodB国) 开环系统对数频率特性(Bode) 接下来. 频率特性的基本概念 。场率特性()的定义 ▣频率特性G(w)的图解表示 对数频率特性(Bode图) 。典型环节的Boe图 ·开环系统对数频率特性(Bode) 幅相频率特性(Nyquist图) 。典型环节的幅相频率特性 系统开环幅相曲线 频域稳定判据 。帽角原理 。奈奎斯特稳定判据 对数稳定判据 稳定裕度 。稳定裕度的定义 。稳定裕度的计算 1口。t,花1三至分0C 第五章线性系统的过分折 自动控制原理 电子信息学院201118
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 对数频率特性(Bode 图) 开环系统对数频率特性 ( Bode) 接下来... 1 频率特性的基本概念 频率特性 G(jω) 的定义 频率特性 G(jω) 的图解表示 2 对数频率特性(Bode 图) 典型环节的 Bode 图 开环系统对数频率特性 ( Bode) 3 幅相频率特性(Nyquist 图) 典型环节的幅相频率特性 系统开环幅相曲线 4 频域稳定判据 幅角原理 奈奎斯特稳定判据 对数稳定判据 5 稳定裕度 稳定裕度的定义 稳定裕度的计算 6 利用开环频率特性分析系统的性能 7 利用闭环频率特性分析系统的性能 用向量法求闭环频率特性 闭环频率特性的几个特征量 第五章 线性系统的频域分析 自动控制原理 电子信息学院 20 / 118