
最优控制理论与系统 第三章极小值原理及其应用 张永韡 江苏科技大学 电子信息学院 yongwzhang@gmail.com November 9,2016 4口+44在4使定)0G
最优控制理论与系统 第三章 极小值原理及其应用 张永韡 江苏科技大学 电子信息学院 yongwzhang@gmail.com November 9, 2016 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

本章主要内容 。经典变分法的局限性 。连续系统的极小值原理 。最短时间控制问题 。最少燃料控制问题 。离散系统的极小值原理 。小结 1口。1,4之1三,至分只C 三章极小位卓建及其应用 最优控制理论与系统 November 9.2016 2/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 本章主要内容 经典变分法的局限性 连续系统的极小值原理 最短时间控制问题 最少燃料控制问题 离散系统的极小值原理 小结 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 2 / 67

经典变分法的园限性 经典变分法的局限性 上面我们用经典变分法解最优控制问题时,得出了最优性的必要条件 ∂H aU =0 在得出这个条件时,作了下面的假定: ●6U是任意的,即不受限制,它遍及整个向量空间,是一个开集; 。號是存在的。 口·40,工1三型分00 三章极小值原理及其应用 最优控制理论与系统 November 9,2016 3/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 经典变分法的局限性 经典变分法的局限性 上面我们用经典变分法解最优控制问题时,得出了最优性的必要条件 ∂H ∂U = 0 在得出这个条件时,作了下面的假定: 1 δU 是任意的,即不受限制,它遍及整个向量空间,是一个开集; 2 ∂H ∂U 是存在的。 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 3 / 67

经典变分法的局限性 在实际工程问题中,控制作用常常是有界的。如飞机舵面的偏角有限制, 火箭的推力有限制,生产过程中的生产能力有限制等等。一般,我们可 用下面的不等式来表示 lu(t≤M:i=1,…,m 这时U()=[山(t),(),…,u(t]T属于一个有界的闭集,写成 ()∈2,2为闭集。更一般的情况可用下面的不等式约束来表示。 gUt),≥0 当U(t)属于有界闭集,()在边界上取值时,6U就不是任意的了,因 为无法向边界外取值,这时盟就不一定是最优解的必要条件。 1口。t,花1三:至)只C 三章极小拉原速及其应用 最优控制理论与系统 November 9.2016 4/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 经典变分法的局限性 在实际工程问题中,控制作用常常是有界的。如飞机舵面的偏角有限制, 火箭的推力有限制,生产过程中的生产能力有限制等等。一般,我们可 用下面的不等式来表示 |ui(t)| ≤ Mi i = 1, · · · , m 这时 U(t) = [u1(t), u2(t), · · · , um(t)]T 属于一个有界的闭集,写成 U(t) ∈ Ω,Ω 为闭集。更一般的情况可用下面的不等式约束来表示。 g[U(t), t] ≥ 0 当 U(t) 属于有界闭集,U(t) 在边界上取值时,δU 就不是任意的了,因 为无法向边界外取值,这时 ∂H ∂U 就不一定是最优解的必要条件。 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 4 / 67
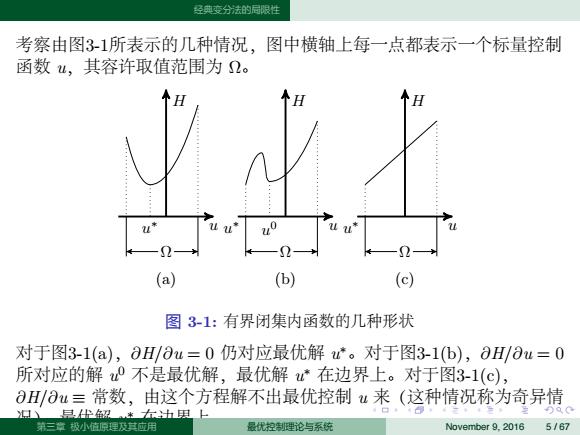
经典变分法的局限性 考察由图3-1所表示的几种情况,图中横轴上每一点都表示一个标量控制 函数山,其容许取值范围为2。 (a) (b) (c) 图3-1:有界闭集内函数的几种形状 对于图3-1(a),aH/au=0仍对应最优解产。对于图3-1(b),aH/au=0 所对应的解0不是最优解,最优解在边界上。对于图3-1(c), 0H/日u=常数,由这个方程解不出最优控制u来(这种情况称为奇异情 ▣小三尘*大h里上 第三章极小值原理及其应用 最优控制理论与系统 November 9,2016 5/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 经典变分法的局限性 考察由图3-1所表示的几种情况,图中横轴上每一点都表示一个标量控制 函数 u,其容许取值范围为 Ω。 u H Ω (a) u H Ω (b) u H Ω (c) u ∗ u ∗ u 0 u ∗ 图 3-1: 有界闭集内函数的几种形状 对于图3-1(a),∂H/∂u = 0 仍对应最优解 u ∗。对于图3-1(b),∂H/∂u = 0 所对应的解 u 0 不是最优解,最优解 u ∗ 在边界上。对于图3-1(c), ∂H/∂u ≡ 常数,由这个方程解不出最优控制 u 来(这种情况称为奇异情 况),最优解 u 第三章 极小值原理及其应用 ∗ 在边界上。 最优控制理论与系统 November 9, 2016 5 / 67