
LSS算法框架 LSS(Neigh)-Local Search Scheme according to a neighborhood Neigh Input:An input instance z of an optimization problem U. Step 1: Eind 2 foasiblo solution) 我们有可能写出 Step 2: while ag LocOPTu(a,Neigh)do begin find a B E Neigh(a)such that 个LocOPTui函数吗? cost(B)<cost(a)if U is a minimization problem and cost(B)>cost(a)if U is a maximization problem;a:=B end Output:output(a)
LSS算法框架 我们有可能写出一 个LocOPTU函数吗?
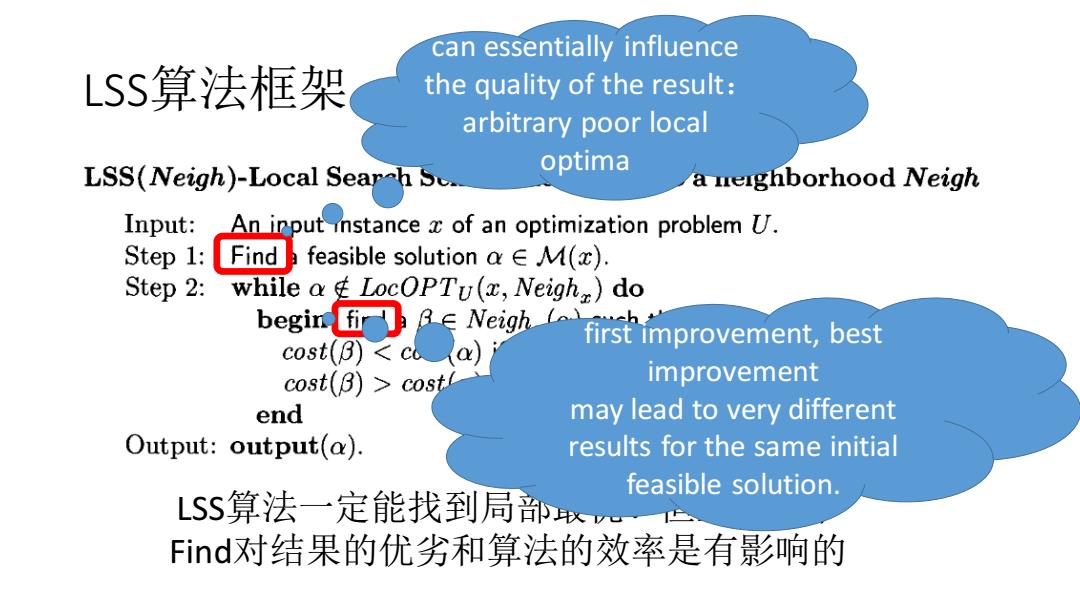
can essentially influence LSS算法框架 the quality of the result: arbitrary poor local LSS(Neigh)-Local Sear h Sc. optima a neighborhood Neigh Input:An input instance x of an optimization problem U. Step 1:Finda feasible solution a E M(x) Step 2:while ag LocOPTu(x,Neigh)do begin fir∈Neigh cost(B)<cla)j first improvement,best cost(B)>cost improvement end may lead to very different Output:output(a). results for the same initial feasible solution. LSS算法一定能找到局部取 Find对结果的优劣和算法的效率是有影响的
LSS算法框架 LSS算法一定能找到局部最优!但上述两个 Find对结果的优劣和算法的效率是有影响的 can essentially influence the quality of the result: arbitrary poor local optima first improvement, best improvement may lead to very different results for the same initial feasible solution

LSS算法的典型示例:爬山算法 E A点、E点出发,结果大相径庭 任何一点出发,我们得到的近邻最优,只保证是极值! 近邻最优,往往是个“陷阱
LSS算法的典型示例:爬山算法 A B C D E F A点、E点出发,结果大相径庭 任何一点出发,我们得到的近邻最优,只保证是极值! 近邻最优,往往是个“陷阱

必须解决局部搜索方法中的 poor local optima”问题 The basic idea of simulated annealing is to add the possibility of leaving a local optimum (i.e.,to move to a weaker solution than the current one)by some kind of coin tossing (random decision)
必须解决局部搜索方法中的 “poor local optima”问题

物理学中的“退火”是什么? (1)The temperature of the heat bath is increased to a maximum value at which the solid melts.This causes all the particles to arrange themselves randomly. (2)The temperature of the heat bath is slowly decreased according to a given cooling schedule until a low-energy state of the solid (a perfect crystal structure)is achieved
物理学中的“退火”是什么?