山东大学：《生物医学信号处理 Biomedical Signal Processing》精品课程教学资源（PPT课件讲稿）Chapter 07 Filter Design Techniques

7.2.1 Filter Design by Impulse Invariance The impulse response of discrete-time system is defined by sampling the impulse response of a continuous-time system. h n =The (nTa) Relationship of two systems in frequency domain: ue)22+2w=n7 fH(2)=0,22π/Ta, then H-I号》b$x i.e.the continuous-time filter in one period is bandlimited,and 2s=22mx 0号 2 29

29 7.2.1 Filter Design by Impulse Invariance ◆The impulse response of discrete-time system is defined by sampling the impulse response of a continuous-time system. ( ) 0, , c d if H j T  =  ( ) ( ), j c d then H e H jT   =    Relationship of two systems in frequency domain: i.e. the continuous-time filter is bandlimited, and Ωs ≥2Ωmax in one period ( ) ( ) 2 , j c k d d H e H j j k T T     =− = +  . Td  = h n T h nT   = d c d ( )  = Td 2 , s Td   =

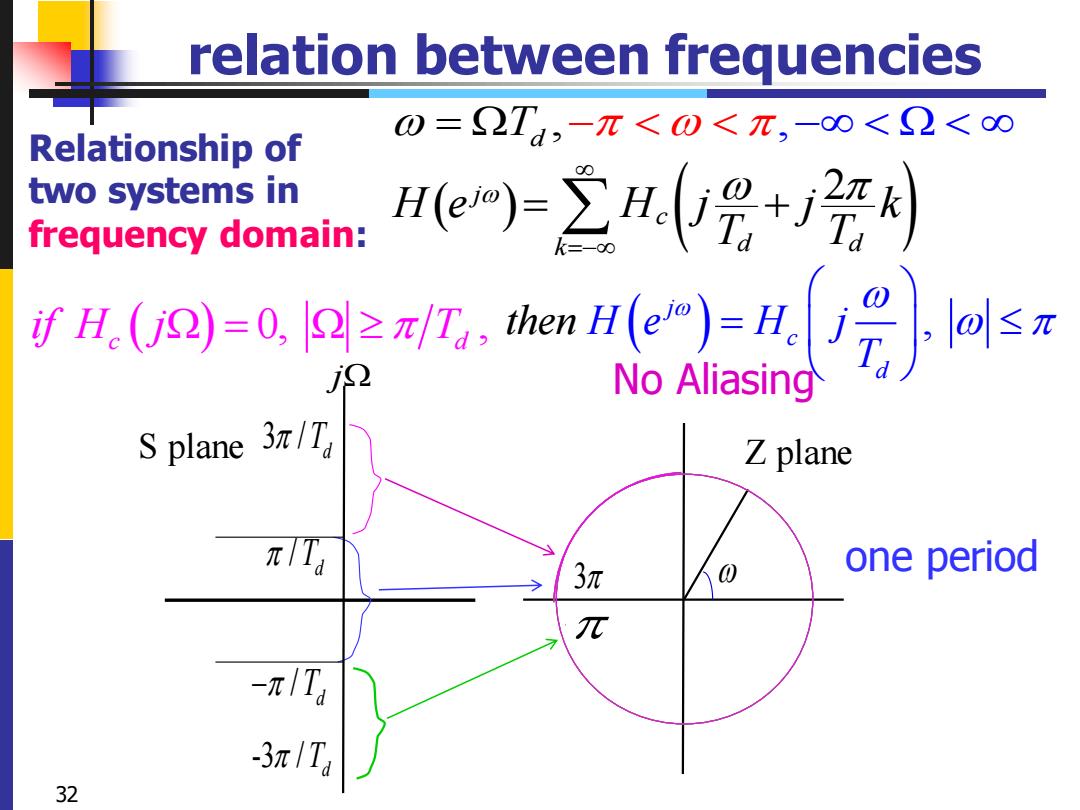
relation between frequencies Relationship of 0=2T,-π<0<π，-∞<2<∞ two systems in frequency domain: e）立V号+ H.(Um=x7,e)号sx No Aliasing S plane 3z/T Z plane πTa 3π 0 one period π -π/Ta -3πT 32

relation between frequencies 32 , ,  = Td −      −     S plane Z plane - 3 / d  T j / d  T / d − T -3 / d  T −   ( ) ( ) j 2 c k d d H e H j j k T T     =− = +  ( ) 0, , c d if H j T  =   ( ) , j c d th T en H H e j       =      one period No Aliasing Relationship of two systems in frequency domain: −3 3- 

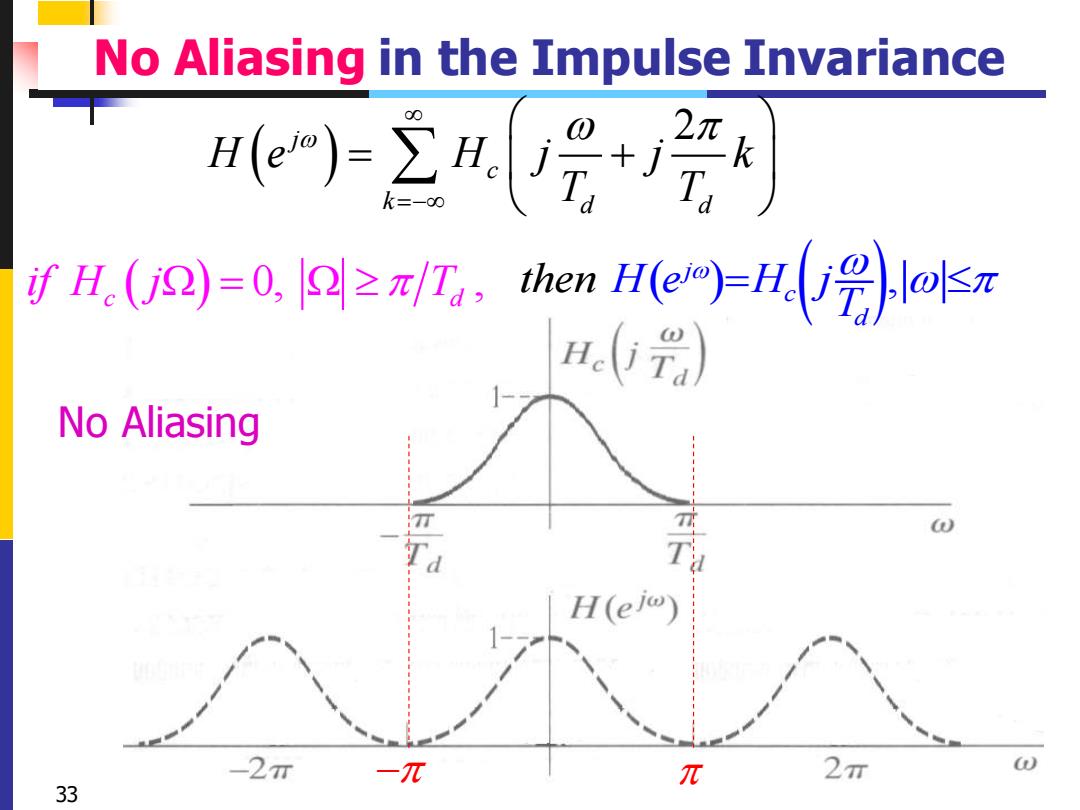
No Aliasing in the Impulse Invariance e个三号+ 2π ifH(2)=0,2≥π/T, then A.0) No Aliasing H(ej) -2π -π π 2n 33

33 No Aliasing in the Impulse Invariance −  ( ) 0, , c d if H j T  =   ( ) ( ), j c d H e H jT then   =    No Aliasing ( ) j 2 c k d d H e H j j k T T     =−   = +     

Aliasing in the Impulse Invariance He)立叱号+受 fH.(2)≠0,2≥π/T, then HH2)体r号 Aliasing -2π/T,/Ta πTa2π/Ta H(e) -2m π 2n 34

34 − Td  Td −  Aliasing in the Impulse Invariance ( ) 0, , c d if H j T     ( ) ( ), j c d H e H jT then       −  2−  Td 2 Td Aliasing ( ) ( ) 2 , j c k d d H e H j j k T T     =− = + 

Aliasing in the Impulse Invariance He)立叱号+受 fH.(2)≠0,2≥π/T, then HH2)体r号 Aliasing -2π/T,/T πT,2π/Ta H(e) -2m 2n

35 −  Aliasing in the Impulse Invariance − Td  Td −  2−  Td 2 Td Aliasing ( ) 0, , c d if H j T     ( ) ( ), j c d H e H jT then       ( ) ( ) 2 , j c k d d H e H j j k T T     =− = +  Aliasing may be ignored in application Design lowpass Filter