
第二章原子的结构和性质 2.2量子数的物理意义 Yzp. n=2,1=1,m=0 Y2p.n=2,1=1,m=0 Y2p,n=2,1=1,m=+1 3d-y=3,1=2 3d 1n=3, 1=2 11
11 x Y2p n = 2, l = 1, m = +1 第二章 原子的结构和性质 2.2 量子数的物理意义 z Y2p n = 2, l = 1, m = 0 2 2pz Y n = 2, l = 1, m = 0 3d 2 2 x − y n=3, l=2 n=3, l=2 xz 3d

第二章原子的结构和性质 2.3波函数和电子云图 径向分布函数 为了计算在半径为r的球面到半径为+d的球面之间薄壳层内 电子出现的概率,引入径向分布函数(①)。 (,0,φ)表示在(,0,φ)处电子的概率密度,因而在 点r,0,p)附近的小体积元dτ中,电子出现的概率为 2(c,0,p)dt。 反映了电子云的分布随半径的变化情况。 D的物理意义是:Ddr代表在半径 为r到r+dr两个球壳夹层内找到电子 的几率,它反映了电子云的分布随半 径r的变化情况。 12
12 D的物理意义是:Ddr代表在半径 为r到r+dr两个球壳夹层内找到电子 的几率,它反映了电子云的分布随半 径r的变化情况。 第二章 原子的结构和性质 2.3 波函数和电子云图 径向分布函数 为了计算在半径为r的球面到半径为r+dr的球面之间薄壳层内 电子出现的概率,引入径向分布函数(D)。 Ψ2 (r,θ,φ)表示在(r,θ,φ)处电子的概率密度,因而在 点(r,θ,φ)附近的小体积元dτ中,电子出现的概率为 Ψ2 (r,θ,φ) dτ。 反映了电子云的分布随半径r的变化情况

第二章原子的结构和性质 2.3波函数和电子云图 ψ(r,B,中)=R(r)⊙(B)Φ(中) 的 d =r2 sin Odrdedp Dah=。2(r,0,)dT -[()(rsin atrdad 的 =r2R2dr0o2 sin ad80ΦcdΦ =r2R2dr D=r2R2 对于s态,ψ只是的 D=r2R2=4ww. 函数,与0、φ无关 13
13 2 2 2 2 2 20 2 0 2 2 2 2 2 0 0 2 2 0 0 2 sin [ ( ) ( ) ( )] sin , , ) sin , , ) ( ) ( ) ( ) D r R r R dr r R dr d d R r r drd d Ddr r d d r drd d r R r = == = == = = = = = π φ πθ π φ πθ ψ ( τ τ ψ( 对于 s态, ψ只是 r 的 函数,与 θ 、 φ无关 第二章 原子的结构和性质 2.3 波函数和电子云图 D 的公式的推导
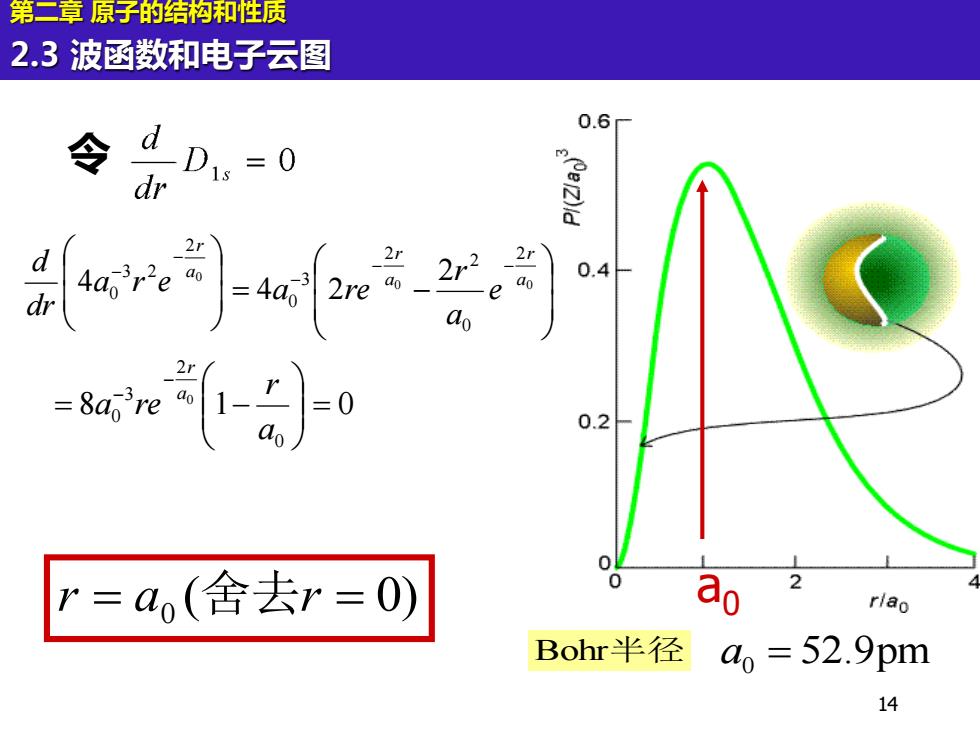
第二章原子的结构和性质 2.3波函数和电子云图 0.6 令 dr 21 2r22 0.4 a -e ao a 0.2 r=a(舍去r=0) 0 ao rlao Bohr半径 a=52.9pm 14
14 第二章 原子的结构和性质 2.3 波函数和电子云图 令 ( 0) r = a0 舍去r = a0 − − 0 2 3 2 4 0 a r a r e dr d = − − − − 0 0 2 0 2 2 3 0 2 4 2 a r a r e a r a re 8 1 0 0 2 3 0 0 = = − − − a r a re a r Bohr半径 a0 = 52.9pm
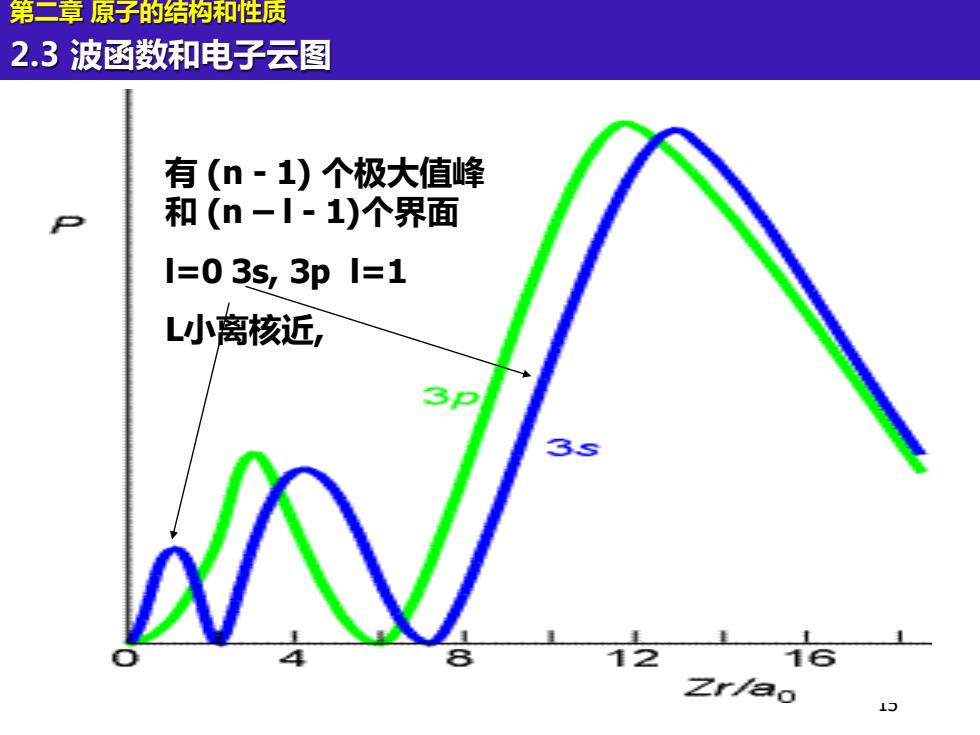
第二章原子的结构和性质 2.3波函数和电子云图 有(n·1)个极大值峰 和(n-I-1)个界面 1=035,3p1=1 L小离核近, 3P 3s 16 Zr/ao
15 第二章 原子的结构和性质 2.3 波函数和电子云图 有 (n - 1) 个极大值峰 和 (n – l - 1)个界面 l=0 3s, 3p l=1 L小离核近