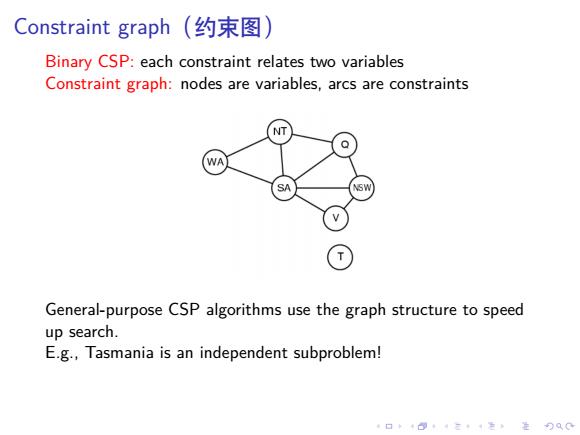
Constraint graph(约束图) Binary CSP:each constraint relates two variables Constraint graph:nodes are variables,arcs are constraints SA General-purpose CSP algorithms use the graph structure to speed up search. E.g.,Tasmania is an independent subproblem! 4口◆4⊙t4三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Constraint graph(约束图) Binary CSP: each constraint relates two variables Constraint graph: nodes are variables, arcs are constraints General-purpose CSP algorithms use the graph structure to speed up search. E.g., Tasmania is an independent subproblem!

Varieties of CSPs Discrete variables ,finite domains有限区域: n variables,domain size dO(d)complete assignments e.g.,Boolean CSPs,incl.Boolean satisfiability (NP-complete) ~infinite domains无限值域(integers,strings,etc.) e.g.,job scheduling,variables are start/end days for each job need a constraint language(约束语言) linear constraints solvable,nonlinear undecidable Continuous variables e.g.,start/end times for Hubble Space Telescope observations linear constraints solvable in polynomial time by linear programming(LP)methods 口卡4三,4色,进分QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Varieties of CSPs ▶ Discrete variables ▶ finite domains 有限区域: ▶ n variables, domain size d → O(d n ) complete assignments ▶ e.g., Boolean CSPs, incl. Boolean satisfiability (NP-complete) ▶ infinite domains 无限值域 (integers, strings, etc.) ▶ e.g., job scheduling, variables are start/end days for each job ▶ need a constraint language(约束语言) ▶ linear constraints solvable, nonlinear undecidable ▶ Continuous variables ▶ e.g., start/end times for Hubble Space Telescope observations ▶ linear constraints solvable in polynomial time by linear programming (LP) methods

Varieties of constraints Unary (constraints involve a single variable, e.g,SA≠green -Binary(二元) constraints involve pairs of variables, eg,SA≠WA Higher-order constraints involve 3 or more variables, e.g,cryptarithmetic(密码算数)column constraints Preferences (soft constraints),e.g.,red is better than green often representable by a cost for each variable assignment 体变量赋值的耗散) constrained optimization problems 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Varieties of constraints ▶ Unary(一元) constraints involve a single variable, e.g., SA ̸= green ▶ Binary(二元) constraints involve pairs of variables, e.g., SA ̸= WA ▶ Higher-order constraints involve 3 or more variables, e.g., cryptarithmetic(密码算数)column constraints ▶ Preferences (soft constraints), e.g., red is better than green often representable by a cost for each variable assignment(个 体变量赋值的耗散) → constrained optimization problems

Example:Cryptarithmetic TWO +T WO FOUR Variables:F T U WR O XX,X3 Domains:{0,1,2,34,5,6,7,8,} Constraints: alldiff (F.T,U,W,R,O) 0+0=R+10·X X1+W+W=U+10·X2 X2+T+T=0+10+X: X3=F,T≠0,F≠0 where X1,X2,and X3 are auxiliary variables representing the digit carried over into the tens,hundreds,or thousands column. 口卡回t·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Example: Cryptarithmetic where X1, X2, and X3 are auxiliary variables representing the digit carried over into the tens, hundreds, or thousands column

Real-world CSPs Assignment problems e.g.,who teaches what class who reviews which papers Timetabling problems e.g.,which class is offered when and where? Hardware configuration Transportation scheduling Factory scheduling Floorplanning(平面布置) Notice that many real-world problems involve real-valued variables 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Real-world CSPs Assignment problems e.g., who teaches what class who reviews which papers Timetabling problems e.g., which class is offered when and where? Hardware configuration Transportation scheduling Factory scheduling Floorplanning(平面布置) Notice that many real-world problems involve real-valued variables