
Constraint satisfaction problems(CSPs) Standard search problem: state is a "black box"-any old data structure that supports goal test,eval,successor 任何可以由目标测试、评价函数、后继函数访问的数据结构 CSP: state is defined by Xi with values from domain (Di goal test is a set of constraints specifying allowable combinations of values for subsets of variables 每个约束包括一些变量的子集,并指定这些子集的值之间允 许进行的合并 Simple example of a formal representation language(形式化 表示方法) ~Allows useful general-purpose(通用的,而不是问题特定 algorithms with more power than standard search algorithms 口卡回t·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Constraint satisfaction problems (CSPs) ▶ Standard search problem: ▶ state is a “black box” –– any old data structure that supports goal test, eval, successor 任何可以由目标测试、评价函数、后继函数访问的数据结构 ▶ CSP: ▶ state is defined by Xi with values from domain(值域) Di ▶ goal test is a set of constraints specifying allowable combinations of values for subsets of variables 每个约束包括一些变量的子集,并指定这些子集的值之间允 许进行的合并 ▶ Simple example of a formal representation language (形式化 表示方法) ▶ Allows useful general-purpose (通用的,而不是问题特定 的) algorithms with more power than standard search algorithms

Constraint satisfaction problems(CSPs) A constraint satisfaction problem(CSP)consists of three components,&D,and C: is a set of variables,{X1,...,Xn} D is a set of domains,[D1,...,Dn},one for each variable Each domain D;consists of a set of allowable values, [v1,...,vk}for variable Xi. C is a set of constraints that specify allowable combinations of values Each constraint Ci consists of a pair(scope,rel,where scope is a tuple of variables that participate in the constraint and rel is a relation that defines the values that those variables can take on A relation can be represented as an explicit list of all tuples of values that satisfy the constraint,or as an abstract relation that supports two operations:testing if a tuple is a member of the relation and enumerating the members of the relation 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Constraint satisfaction problems (CSPs) A constraint satisfaction problem (CSP) consists of three components, X , D, and C: ▶ X is a set of variables, {X1, . . . , Xn} ▶ D is a set of domains, {D1, . . . , Dn}, one for each variable ▶ Each domain Di consists of a set of allowable values, {v1, . . . , vk} for variable Xi . ▶ C is a set of constraints that specify allowable combinations of values ▶ Each constraint Ci consists of a pair ⟨scope,rel⟩, where scope is a tuple of variables that participate in the constraint and rel is a relation that defines the values that those variables can take on ▶ A relation can be represented as an explicit list of all tuples of values that satisfy the constraint, or as an abstract relation that supports two operations: testing if a tuple is a member of the relation and enumerating the members of the relation

Constraint satisfaction problems(CSPs) To solve a CSP,we need to define a state space and the notion of a solution Each state in a CSP is defined by an assignment of values to some or all of the variables,Xi=vi,Xj=vj,... An assignment that does not violate any constraints is called a consistent or legal assignment A complete assignment is one in which every variable is assigned A partial assignment is one that assigns values to only some of the variables A solution to a CSP is a consistent,complete assignment 口卡回t·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Constraint satisfaction problems (CSPs) To solve a CSP, we need to define a state space and the notion of a solution ▶ Each state in a CSP is defined by an assignment of values to some or all of the variables, {Xi = vi , Xj = vj , . . .} ▶ An assignment that does not violate any constraints is called a consistent or legal assignment ▶ A complete assignment is one in which every variable is assigned ▶ A partial assignment is one that assigns values to only some of the variables ▶ A solution to a CSP is a consistent, complete assignment
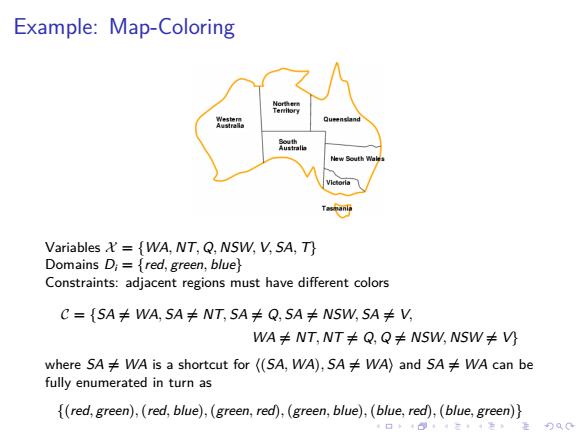
Example:Map-Coloring unne Variables={WA,NT,Q,NSW,V,SA,T} Domains D;=red,green,blue Constraints:adjacent regions must have different colors C={SA≠WA,5A≠NT,SA≠Q,5A≠NSW,SA≠V, WA≠NT,NT≠Q,Q≠NSw,NSW≠ where SA≠WA is a shortcut for(SA,WA),SA≠WA)and SA≠WA can be fully enumerated in turn as (red,green),(red,blue),(green,red),(green,blue),(blue,red),(blue,green)) 2ac
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Example: Map-Coloring Variables X = {WA, NT, Q, NSW, V, SA, T} Domains Di = {red, green, blue} Constraints: adjacent regions must have different colors C = {SA ̸= WA, SA ̸= NT, SA ̸= Q, SA ̸= NSW, SA ̸= V, WA ̸= NT, NT ̸= Q, Q ̸= NSW, NSW ̸= V} where SA ̸= WA is a shortcut for ⟨(SA, WA), SA ̸= WA⟩ and SA ̸= WA can be fully enumerated in turn as {(red, green),(red, blue),(green,red),(green, blue),(blue,red),(blue, green)}

Example:Map-Coloring Ta呼 Solutions are assignments satisfying all constraints,e.g., {WA=red,NT=green,Q=red,NSW=green,V=red, SA=blue,T=green} 口·三色,进分双0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Example: Map-Coloring Solutions are assignments satisfying all constraints, e.g., {WA = red, NT = green, Q = red, NSW = green, V = red, SA = blue,T = green}