
3.求球面x2+y2+z2=a2与圆柱面x2+y2=x(a>0)所围成的体积 (指含在柱体内部分) 所围立体是曲顶柱体 :1z=Va2-r2 先选系 柱面坐标 下底:z=-√a2-r2 1 r≤ac0sB r =a cose V=4∬Va2-r2rdrd0 D D 4 do fm rdr ia x -a(-sin'onao 怎么计算? 用瓦里斯公式■ =2肾 合
Dxy: 。 。 a 2 2 z a r r =a cos 0 y x 2 0 3 3 (1 sin )d 3 4 π a θ θ a ) 9 4 3 2 ( 3 4 d d 2 0 cos 0 2 2 π a θ θ a r r r r acos 。 所围立体是曲顶柱体 V (指含在柱体内部分) 求球面 与圆柱面 ) 所围成的体积 ( x y z a x y ax a : 上顶 下底: 2 2 z a r D 怎么计算? 用瓦里斯公式 先选系 柱面坐标 a r rdrd D . 3
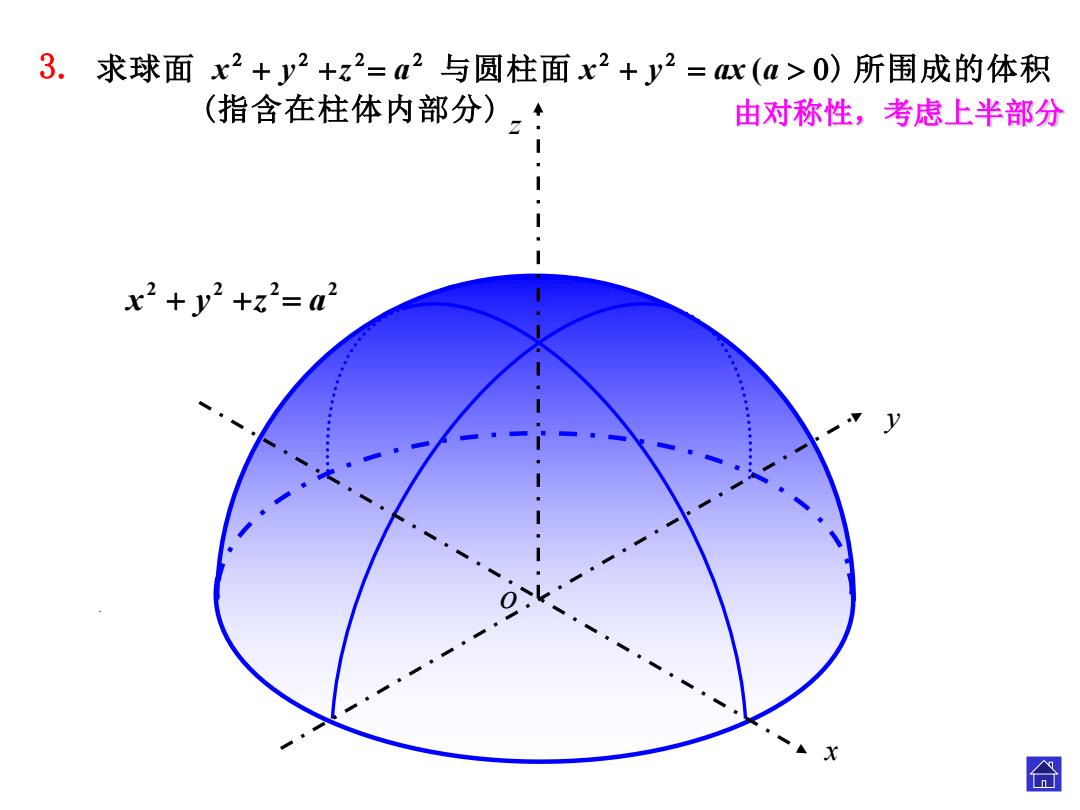
3.求球面x2+y2+z2=a2与圆柱面x2+y2=心(a>0)所围成的体积 (指含在柱体内部分)。· 由对称性,考虑上半部分 x2+y2+z2=a2 X 合
(指含在柱体内部分) 求球面 与圆柱面 ) 所围成的体积 ( x y z a x y ax a 2 2 2 2 x y z a z 由对称性,考虑上半部分 x y . o 3
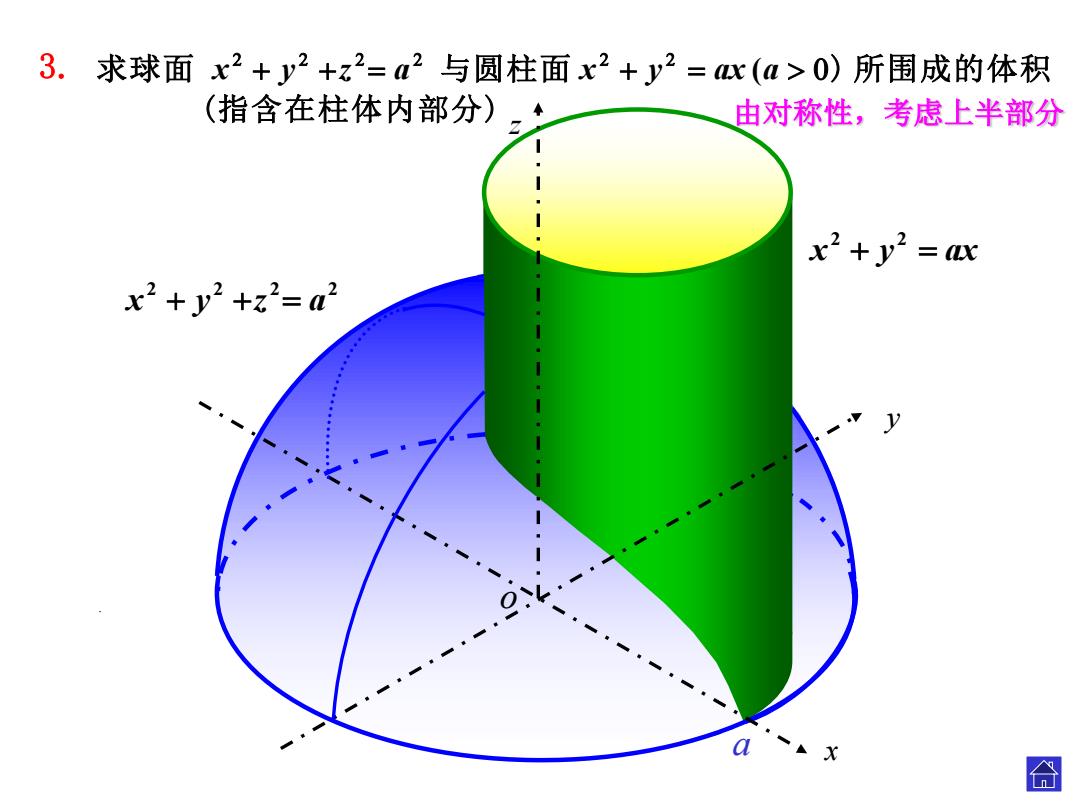
3.求球面x2+y2+z2=a2与圆柱面x2+y2=(a>0)所围成的体积 (指含在柱体内部分)。◆ 由对称性,考虑上半部分 x2+y2= x2+y2+z2=a2 合
(指含在柱体内部分) 求球面 与圆柱面 ) 所围成的体积 ( x y z a x y ax a a 2 2 2 2 x y z a 2 2 x y ax 由对称性,考虑上半部分 . 3. x y o z
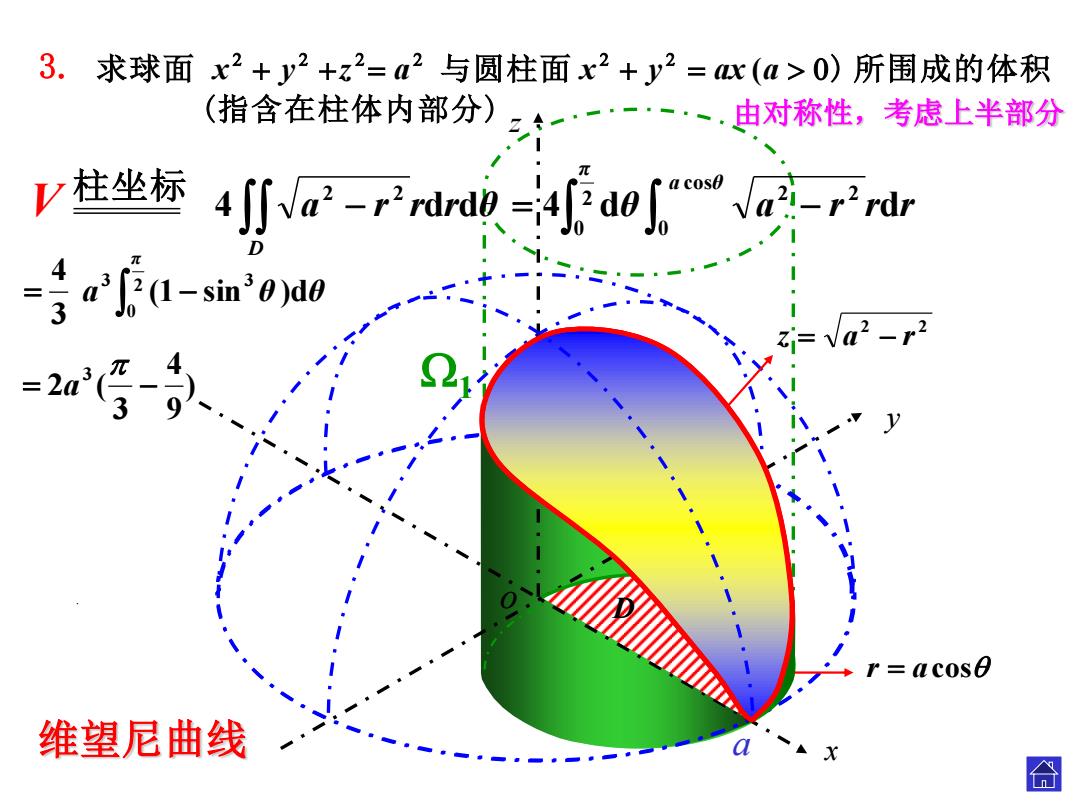
3.求球面x2+y2+z2=a2与圆柱面x2+y2=心(a>0)所围成的体积 (指含在柱体内部分) 一·一·一·一·、.由对称性,考虑上半部分 V柱坐标 4∬a2-rtbd0a2-rPir D 有ou-smoa0 zi=va2-r2 2 20 =acose 维望尼曲线
(指含在柱体内部分) 求球面 与圆柱面 ) 所围成的体积 ( x y z a x y ax a z = 0 a x y z o 柱坐标 。 V 2 0 3 3 (1 sin )d 3 4 π a θ θ a ) 9 4 3 2 ( 3 a r r r θ D 4 d d 2 2 2 2 z a r 。 r acos 。 。 维望尼曲线 4 d d。 2 0 cos 0 2 2 π a θ θ a r r r 。 由对称性,考虑上半部分 D 1 . 3
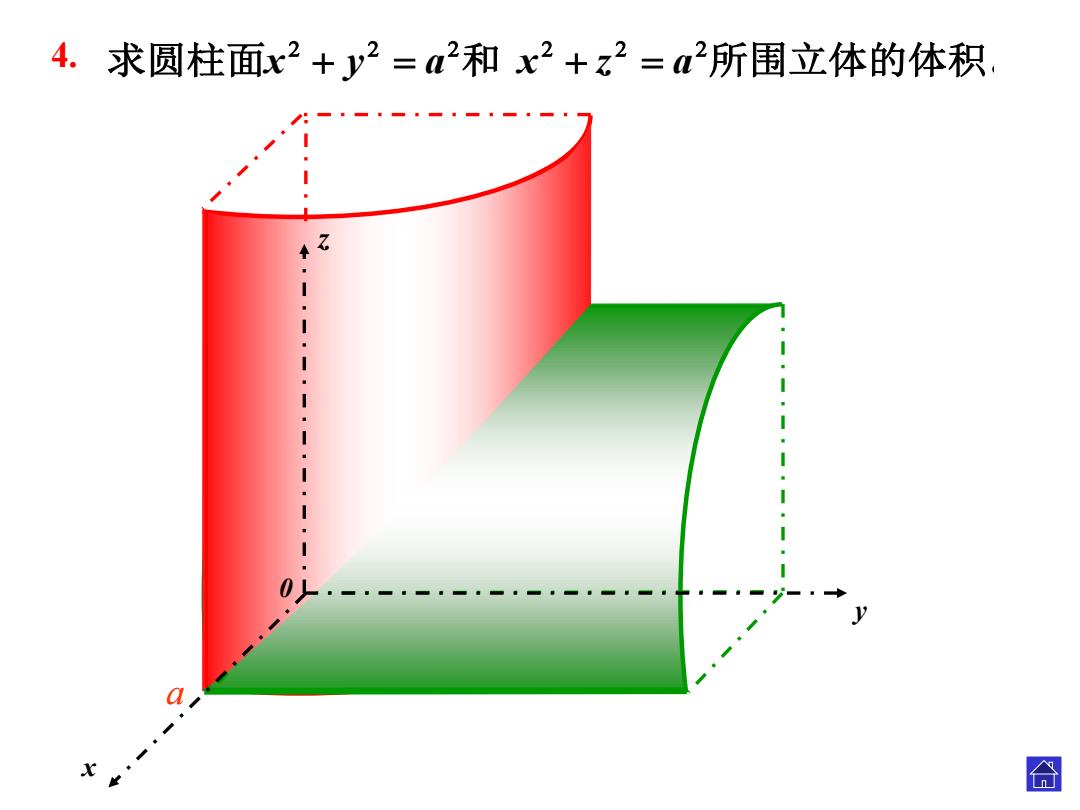
4.求圆柱面x2+y2=2和x2+z2=a2所围立体的体积. y X-、 合
a a x z y 0 4. 求圆柱面x y a 和 x z a 所围立体的体积