
山东理工大客$ 11.3化学反应的速率方程SHANDONGUNIVERSITYOFTECHNOLOGY基元反应和非基元反应的反应历程为(3) H, +Br, = 2HBr(10) Br, + M →2Br·+M+(11) Br+H, →HBr +H(12) H+Br, → HBr + Br(13) H+HBr → H, + Br:(14) Br·+Br·+M → Br, + M
22 基元反应和非基元反应 的反应历程为 2 (10) Br M 2Br M + → + 2 (11) Br H HBr H + → + 2 (12) H Br HBr Br + → +2 (14) Br Br M Br M + + → + 2 (13) H HBr H Br + → + 2 2 (3) H Br 2HBr + = §11.3 化学反应的速率方程

山东理工大客S 11.3化学反应的速率方程SHANDONGUNIVERSITYOFTECHNOLOGY基元反应和非基元反应基元反应简称元反应。如果一个化学反应,反应物分子在碰撞中相互作用,在一次化学行为中就能转化为生成物分子,这种反应称为基元反应,例如上述反应历程中,(4)-(14)的反应都是基元反应。如果一个化学计量式代表了若于个基元反应的总结果,那这种反应称为总包反应或总反应,是非基元反应
23 基元反应和非基元反应 基元反应简称元反应。如果一个化学反应,反应 物分子在碰撞中相互作用,在一次化学行为中就能 转化为生成物分子,这种反应称为基元反应。 例如上述反应历程中,(4)-(14)的反应都是基 元反应。 如果一个化学计量式代表了若干个基元反应的 总结果,那这种反应称为总包反应或总反应,是 非基元反应。 §11.3 化学反应的速率方程

山东理工大客$ 11.3化学反应的速率方程SHANDONGUNIVERSITYOFTECHNOLOGY反应机理(reaction mechanism)反应机理又称为反应历程。在总反应中,连续或同时发生的所有基元反应称为反应机理,在有些情况下,反应机理还要给出所经历的每一步的立体化学结构图。同一反应在不同的条件下,可有不同的反应机理。了解反应机理可以掌握反应的内在规律,从而更好的驾驭反应
24 反应机理(reaction mechanism) 反应机理又称为反应历程。在总反应中,连续 或同时发生的所有基元反应称为反应机理,在有些 情况下,反应机理还要给出所经历的每一步的立体 化学结构图。 同一反应在不同的条件下,可有不同的反应机 理。了解反应机理可以掌握反应的内在规律,从而 更好的驾驭反应。 §11.3 化学反应的速率方程
山东理工大客$ 11.3化学反应的速率方程SHANDONGUNIVERSITYOFTECHNOLOGY质量作用定律(law of mass action)基元反应的速率与反应物浓度(含有相应的指数)的乘积成正比。浓度的指数就是基元反应方程中各反应物的计量系数。这就是质量作用定律,它只适用于基元反应。例如:基元反应反应速率r(1) Cl, +M= 2Cl+ Mk,[C1, J[M](2) Cl + H2 =HCl+Hk,[C]][H, ](3) H+Cl2 = HCl+CIk,[H][C12 ](4) 2k4[C]?[M]2Cl+M = Cl, + M
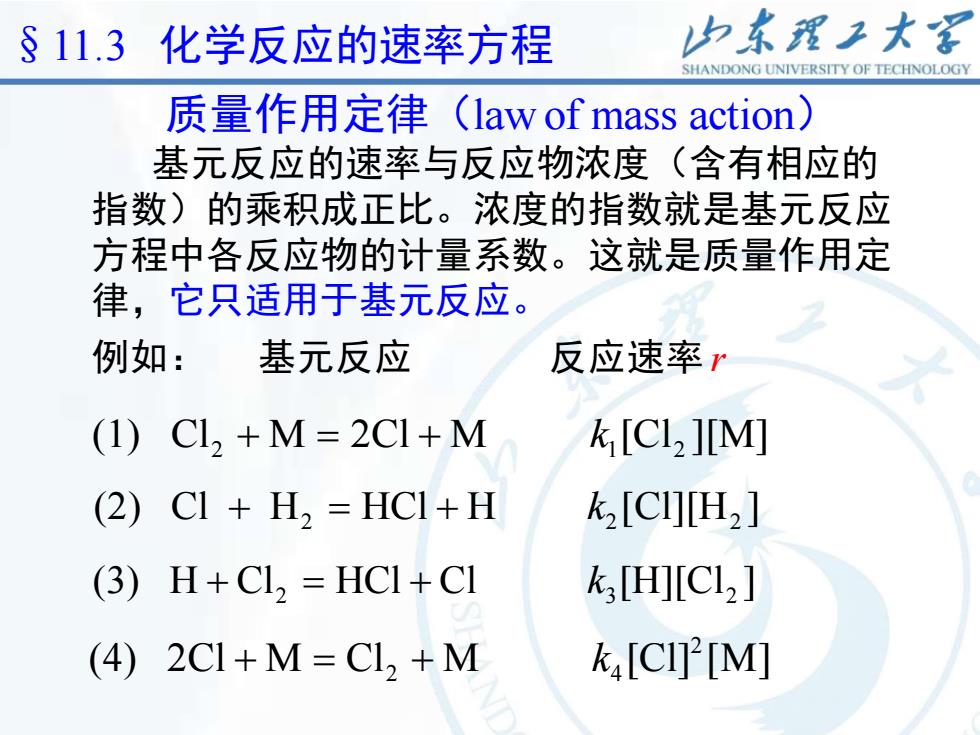
25 质量作用定律(law of mass action) 基元反应的速率与反应物浓度(含有相应的 指数)的乘积成正比。浓度的指数就是基元反应 方程中各反应物的计量系数。这就是质量作用定 律,它只适用于基元反应。 2 1 2 (1) Cl M 2Cl M [Cl ][M] + = + k 例如: 基元反应 反应速率 r 2 2 2 (2) Cl H HCl H [Cl][H ] + = + k 2 3 2 (3) H Cl HCl Cl [H][Cl ] + = + k 2 2 4 (4) 2Cl M Cl M [Cl] [M] + = + k §11.3 化学反应的速率方程

山东理工大客S 11.3化学反应的速率方程SHANDONGUNIVERSITYOFTECHNOLOGY反应的级数、反应分子数和反应的速率常数速率方程中,各反应物浓度项上的指数称为该反应物的级数;所有浓度项指数的代数和称为该反应的总级数通常用n表示。n的大小表明浓度对反应速率影响的大小。反应级数可以是正数、负数、整数、分数或零有的反应无法用简单的数字来表示级数反应级数是由实验测定的
26 反应的级数、反应分子数和反应的速率常数 速率方程中,各反应物浓度项上的指数称为该 反应物的级数; 所有浓度项指数的代数和称为该反应的总级数, 通常用n 表示。 反应级数可以是正数、负数、整数、分数或零, 有的反应无法用简单的数字来表示级数。 反应级数是由实验测定的。 n 的大小表明浓度对反应速率影响的大小。 §11.3 化学反应的速率方程