
(⑤)解题过程 ·定义状态描述,定义一组算符 ·问题的求解过程是一个不断把算符作用于 状态的过程 ·算符的一次使用,就使问题由一种状态转 变为另一种状态,使用算符最少的解称为 最优解 ·对任何一个状态,可使用的算符不止一个, 生成的后继状态可能有多个,涉及搜索策 略
(5)解题过程 • 定义状态描述,定义一组算符 • 问题的求解过程是一个不断把算符作用于 状态的过程 • 算符的一次使用,就使问题由一种状态转 变为另一种状态,使用算符最少的解称为 最优解 • 对任何一个状态,可使用的算符不止一个, 生成的后继状态可能有多个,涉及搜索策 略

3与/或树表示法:用于比校复杂的问题 (1)分解:问题分解为子问题,子问题分解为子问题 例P分解成P1,P2,P3三个子问题,只有当这三个 子问题都可以解时,问题P才可解。P1,P2,P3之 间存在“与”关系,节点P为与节点,用一条弧连 接。 (2)等价变换:对于复杂的问题,还可利用同构或 同态的等价变换,把它变换为若干个较容易求 解的新问题。若新问题中有一个可求解,则原 问题可解。 例P被等价变换为三个新问题P1,P2,P3,任何 一个P1可解,P可解,则P1,P2,P3之间存在或关 系,节点P称为或节点。 将上迷两种方法结合使用,称为“与/或
3 与/或树表示法:用于比较复杂的问题 (1)分解:问题分解为子问题,子问题分解为子问题。 例 P分解成P1,P2,P3三个子问题,只有当这三个 子问题都可以解时,问题P才可解。P1,P2,P3之 间存在“与”关系,节点P为与节点,用一条弧连 接。 (2)等价变换:对于复杂的问题,还可利用同构或 同态的等价变换,把它变换为若干个较容易求 解的新问题。若新问题中有一个可求解,则原 问题可解。 例 P被等价变换为三个新问题P1,P2,P3 ,任何 一个Pi可解,P可解,则P1,P2,P3之间存在或关 系,节点P称为或节点。 将上述两种方法结合使用,称为“与/或” 树
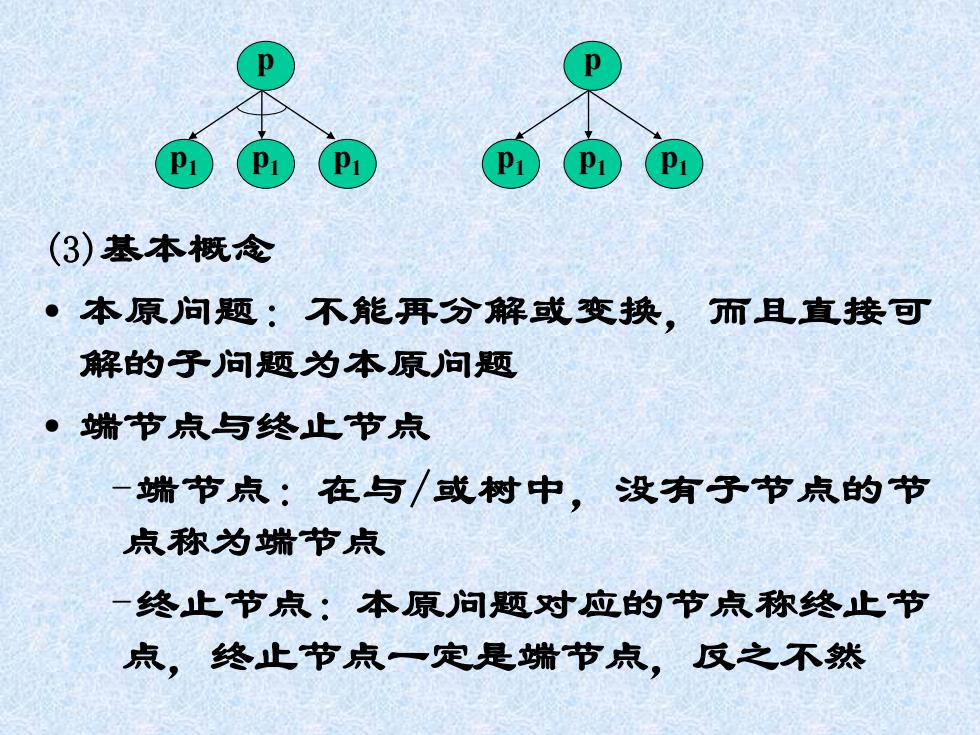
(3)基本概念 ·本原问题:不能再分解或变换,而且直接可 解的子问题为本原问题 ·端节点与终止节点 一端节点:在与或树中,没有子节点的节 点称为端节点 一终止节点:本原问题对应的节点称终止节 点,终止节点一定是蜡节点,反之不然
(3)基本概念 • 本原问题:不能再分解或变换,而且直接可 解的子问题为本原问题 • 端节点与终止节点 –端节点:在与/或树中,没有子节点的节 点称为端节点 –终止节点:本原问题对应的节点称终止节 点,终止节点一定是端节点,反之不然 p p1 p1 p1 p p1 p1 p1

·可解节点:满足下列条件之一 它是一个终止节点 它是一个“或”节点,且子 节点中至少有一个可解节点 -它是一个“与”节点,且子 节点全部是可解节点 ·不可解节点:关于可解节点的 三个条件全部不满足的节点称 为不可解节点 ·解树:由可解节点构成,并且 由这些可解节点推出初始节点 (原始问题)为可解节点的子 树称为解树,解树中一定包含 初始节点
• 可解节点:满足下列条件之一 –它是一个终止节点 –它是一个“或”节点,且子 节点中至少有一个可解节点 –它是一个“与”节点,且子 节点全部是可解节点 • 不可解节点:关于可解节点的 三个条件全部不满足的节点称 为不可解节点 • 解树:由可解节点构成,并且 由这些可解节点推出初始节点 (原始问题)为可解节点的子 树称为解树,解树中一定包含 初始节点。 p t t t t t t t

例三阶梵塔问题 初始状态:三片金片都在1号针上 目标状态:三片金片都在3号针上 要求:小片在大片之上 分析:原问题由三个子问题 1把金片A及B移到2号针的双金片问题一分解3个子 问题 2把金片C移到3号针的单金片问题 3把金片A及B移到3号针的双金片问题一分解3个子 问题 设三元组(i,j,k) 金片C针号 金片B针号 金片A针号
例 三阶梵塔问题 初始状态:三片金片都在1号针上 目标状态:三片金片都在3号针上 要求:小片在大片之上 分析:原问题由三个子问题 1 把金片A及B移到2号针的双金片问题—分解3个子 问题 2 把金片C移到3号针的单金片问题 3 把金片A及B移到3号针的双金片问题—分解3个子 问题 设 三元组(i,j,k) 金片C针号 金片B针号 金片A针号