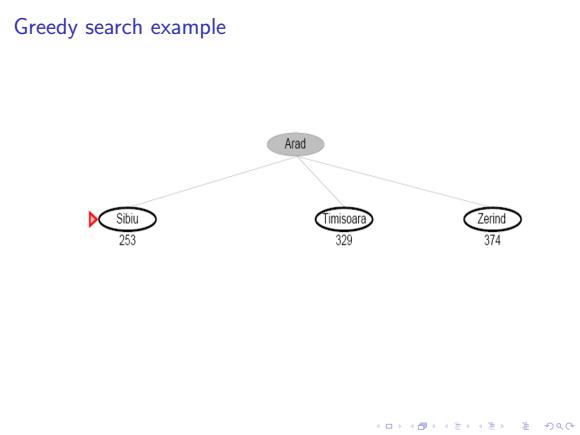
Greedy search example Arad ( Sibiu Timisoara Zerind 253 329 374 口卡B·三4色进分双0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Greedy search example
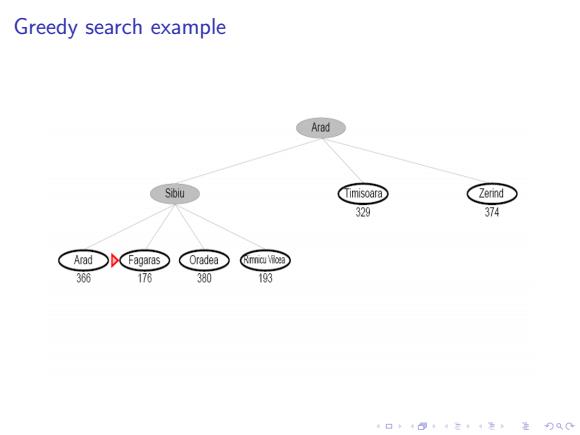
Greedy search example Arad Sibiu Timisoara Zerind 329 374 Arad Fagaras Oradea RmnicuVBoea 36 176 380 193 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Greedy search example
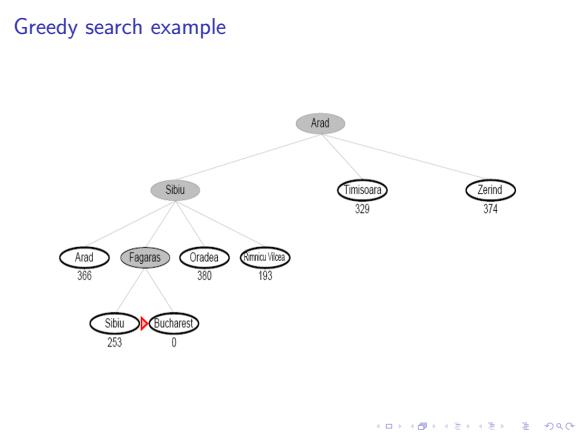
Greedy search example ad● Sibiu limisoara Zerind 329 374 Arad Fagaras 0r809a Rmncu Vicea 386 380 193 Sibiu Bucharest 253 口卡回t·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Greedy search example

Properties of greedy search complete?No-can get stuck in loops,e.g.from lasi to Fagaras, lasi→Neamt-→lasi-→Neamt→ Complete in finite space with repeated-state checking Time?O(bm),but a good heuristic can give dramatic improvement Space?O(bm)-keeps all nodes in memory b:Branch factor,d:Solution depth,m:Maximum depth Optimal?No 0 G u464三+1声,量QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Properties of greedy search complete? No — can get stuck in loops, e.g. from Iasi to Fagaras, Iasi→ Neamt→Iasi→ Neamt → Complete in finite space with repeated-state checking Time? O(b m), but a good heuristic can give dramatic improvement Space? O(b m) — keeps all nodes in memory b: Branch factor, d: Solution depth, m: Maximum depth Optimal? No
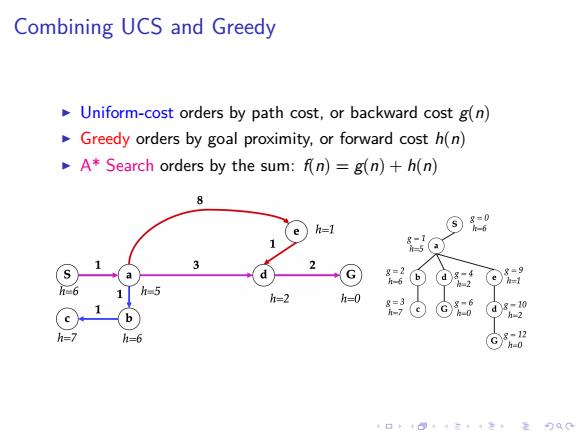
Combining UCS and Greedy Uniform-cost orders by path cost,or backward cost g(n) Greedy orders by goal proximity,or forward cost h(n) A*Search orders by the sum:f(n)=g(n)+h(n) 8 =1 ⊙品 '0 3 ⊙@ ⊙9 t=6 h5 h=2 h=0 ⊙⊙6 ⊙9 h=7 h=6 ⊙ 口卡回t·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Combining UCS and Greedy ▶ Uniform-cost orders by path cost, or backward cost g(n) ▶ Greedy orders by goal proximity, or forward cost h(n) ▶ A* Search orders by the sum: f(n) = g(n) + h(n)