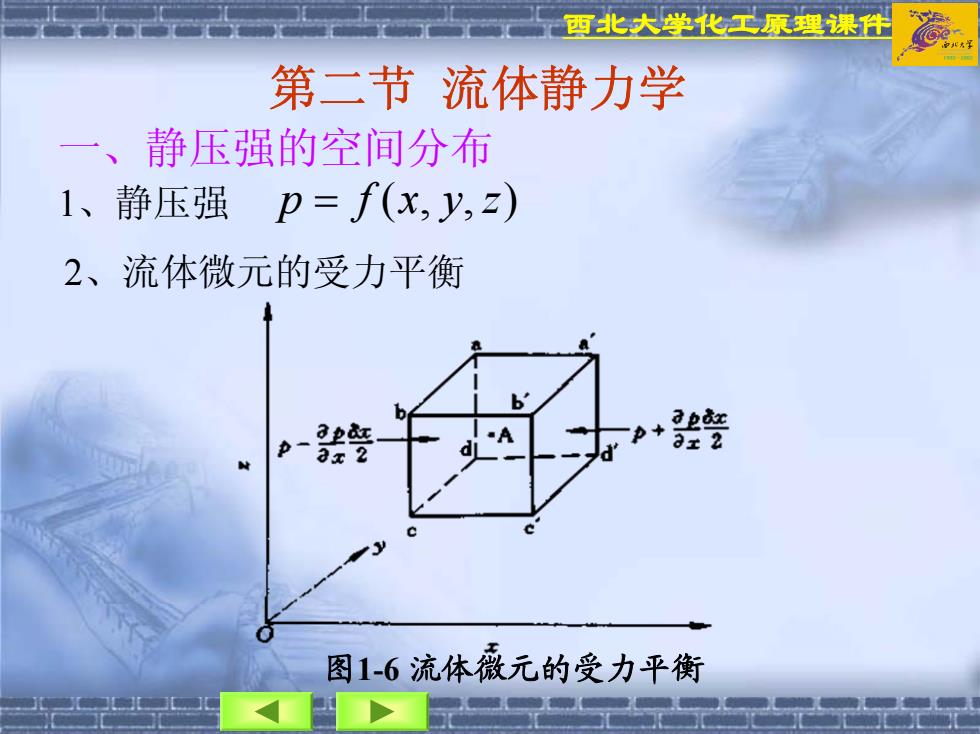
西北大学化工原理课件 第二节 流体静力学 一、静压强的空间分布 1、静压强 = zyxfp ),( 2、流体微元的受力平衡 图1-6 流体微元的受力平衡
西北大学化工原理课件 第二节 流体静力学 一、静压强的空间分布 1、静压强 = zyxfp ),( 2、流体微元的受力平衡 图1-6 流体微元的受力平衡

西北大学化工原理课件 1)表面力 六面体中心点A处的静压强为P,沿x方向作用于 abcd和a'b'c'd'面上的压力分别是 dzdydx x P Pdzdydx x P P ) 21 () 21 ( ∂∂ + ∂∂ − 和 2)体积力 设作用于单位质量流体上的体积力在 x、y、z 方向的分量分别为X、Y、Z
西北大学化工原理课件 1)表面力 六面体中心点A处的静压强为P,沿x方向作用于 abcd和a'b'c'd'面上的压力分别是 dzdydx x P Pdzdydx x P P ) 21 () 21 ( ∂∂ + ∂∂ − 和 2)体积力 设作用于单位质量流体上的体积力在 x、y、z 方向的分量分别为X、Y、Z

西北大学化工原理课件 对于静止流体,外力之和必等于零,如对x方向有: 1 1 ( )( ) 0 2 2 P P P dx dzdy P dx dzdy X dxdydz x x ρ ∂ ∂ − −+ + = ∂ ∂ 微元所受的体积力在x, y, z方向的分量分别为: ( ) X ρdxdydz ( ) Y dxdydz ρ ( ) Z dxdydz ρ
西北大学化工原理课件 对于静止流体,外力之和必等于零,如对x方向有: 1 1 ( )( ) 0 2 2 P P P dx dzdy P dx dzdy X dxdydz x x ρ ∂ ∂ − −+ + = ∂ ∂ 微元所受的体积力在x, y, z方向的分量分别为: ( ) X ρdxdydz ( ) Y dxdydz ρ ( ) Z dxdydz ρ

西北大学化工原理课件 简化得: 同理得: 1 0 p X ρ x ∂ − = ∂ 1 0 p Y ρ y ∂ − = ∂ 1 0 p Z ρ z ∂ − = ∂ 对上列方程组作适当处理得: dz ( ) ZdzYdyXdx z p dy y p dx x p ++= ∂ ∂ + ∂ ∂ + ∂ ∂ ρ 从而得流体平衡方程的一般表达式: dp Xdx Ydy Zdz ρ = ++ 欧拉平衡方程 流体平衡的一般表达式
西北大学化工原理课件 简化得: 同理得: 1 0 p X ρ x ∂ − = ∂ 1 0 p Y ρ y ∂ − = ∂ 1 0 p Z ρ z ∂ − = ∂ 对上列方程组作适当处理得: dz ( ) ZdzYdyXdx z p dy y p dx x p ++= ∂ ∂ + ∂ ∂ + ∂ ∂ ρ 从而得流体平衡方程的一般表达式: dp Xdx Ydy Zdz ρ = ++ 欧拉平衡方程 流体平衡的一般表达式

西北大学化工原理课件 流体平衡方程在重力场的应用 X=0, Y=0, Z=-g 将此代入平衡方程式.得: 设流体不可压缩,即密度ρ与压力无关,可将上式 积分得: 流体静力学基本方程式 p gz ρ + =常数 0 0 dp gdz dp g dz ρ ρ + = + = ∫ ∫
西北大学化工原理课件 流体平衡方程在重力场的应用 X=0, Y=0, Z=-g 将此代入平衡方程式.得: 设流体不可压缩,即密度ρ与压力无关,可将上式 积分得: 流体静力学基本方程式 p gz ρ + =常数 0 0 dp gdz dp g dz ρ ρ + = + = ∫ ∫