在脉冲下结构的响应 9<七) C×(C> ×(C+七)
在脉冲下结构的响应

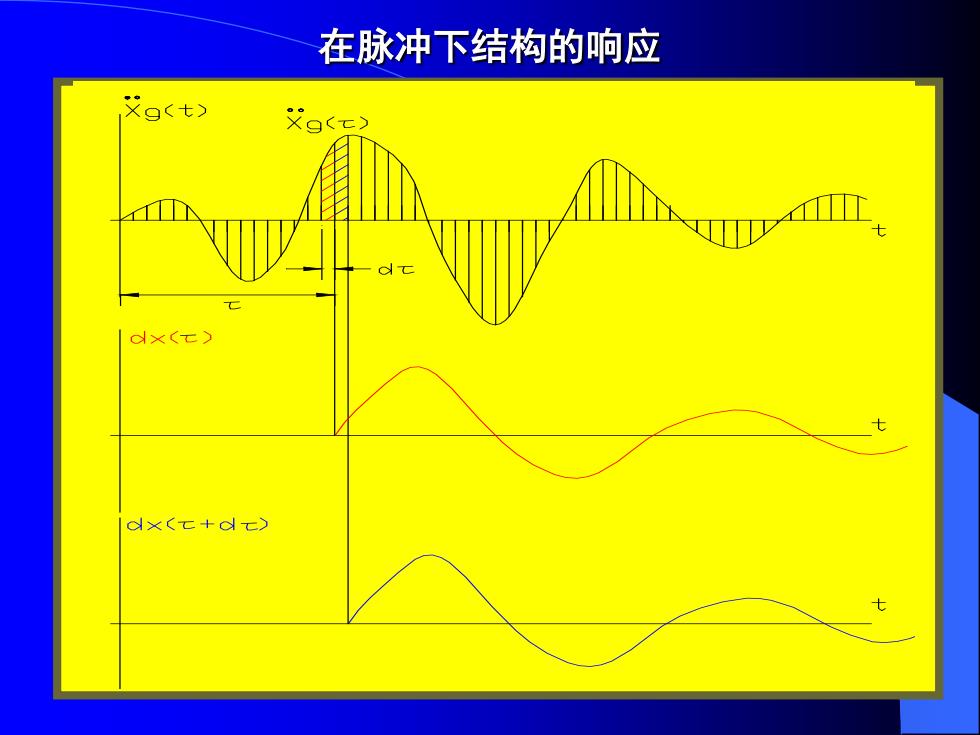
地面运动的加速度戈。曲线是一个不能用数 学表达式表示的曲线。我们可以将其分为无限 个微分脉冲。每一个微分脉冲将产生一个自由 振动(一个位移dx),无限个微分脉冲产生 的位移积分即是方程的特解。 由d时间的脉冲-,(x)d产生的自由振动在t 时刻的位移为: dx(t)e-s([x(t)cos @'(t-t) x(z)+Sox()simo'(t-r】
地面运动的加速度 曲线是一个不能用数 学表达式表示的曲线。我们可以将其分为无限 个微分脉冲。每一个微分脉冲将产生一个自由 振动(一个位移dx ),无限个微分脉冲产生 的位移积分即是方程的特解。 由dt时间的脉冲 产生的自由振动在t 时刻的位移为: g x ( ) g x d ( ) ( ) [ ( )cos '( ) ( ) ( )sin '( )] ' t dx t e x t x x t

初位移 x()三0 初速度 x(x)=-,()x e)=-ea-o,(@ sin@'(t-t)dt 将所有脉冲积分 x(r)=∫dc(x) w=-d。,(ein'u-2ae 非齐次方程的特解也称为杜哈米积分
初位移 初速度 将所有脉冲积分 x( ) 0 ( ) ( ) x x d g ( ) ( ) ( ) sin '( ) ' t g x dx e t d 0 ( ) ( ) t x t dx ( ) 0 1 ( ) ( ) sin '( ) ' t t x t x e t d g —— 非齐次方程的特解也称为杜哈米积分

齐次方程的通解 x(t)=e-s0Ix(0)cos@'t+ x(0)+5ox(0) sin@'t] 非齐次方程的特解 (e-usino't- 非齐次方程的特解与齐次方程的通解相加构成非齐次 方程的通解,一般情况下,初位移和初速度均为零,故 其解为杜哈米积分
非齐次方程的特解与齐次方程的通解相加构成非齐次 方程的通解,一般情况下,初位移和初速度均为零,故 其解为杜哈米积分。 2 (0) (0) ( ) [ (0)cos ' sin ' 1 ' ] ' t x x x t e x t t ( ) 0 1 ( ) ( ) sin '( ) ' t t x t x e t d g 齐次方程的通解 非齐次方程的特解

求出位移反应的解后,微分后还可求出速度 反应。 ()= (e-eos'-)d dt +品天,ae-snou-w 同理可写出加速度反应 进一步求出4=+戈g 得到结构的地震作用
求出位移反应的解后,微分后还可求出速度 反应。 ( ) 0 ( ) 0 ( ) ( ) ( ) cos '( ) ( ) sin '( ) ' t t g t t g dx t x t x e t d dt x e t dt 同理可写出加速度反应 a x xg 进一步求出 a x xg 得到结构的地震作用