
第一节无风险借贷对有马科维兹有效集的影响 无风险资产的定义 二、允许无风险贷款下的投资组合 三、允许无风险借入下的投资组合 四、允许同时进行无风险借贷— 无风险借入和 贷出对有效集的影响
第一节 无风险借贷对有马科维兹有效集的影响 无风险借贷对有马科维兹有效集的影响 一、无风险资产的定义 二、允许无风险贷款下的投资组合 三、允许无风险借入下的投资组合 四、允许同时进行无风险借贷——无风险借入和 贷出对有效集的影响

一、 无风险资产的定义 >在单一投资期的情况下,无风险资产的回报率是 确定的 >无风险资产的标准差为零 >无风险资产的回报率与风险资产的回报率之间的 协方差也是零
一、无风险资产的定义 无风险资产的定义 ¾ 在单一投资期的情况下,无风险资产的回报率是 确定的 ¾ 无风险资产的标准差为零 ¾ 无风险资产的回报率与风险资产的回报率之间的 协方差也是零

>根据定义无风险资产具有确定的回报率, 因此: 口首先,无风险资产必定是某种具有固定收 益,并且没有任何违约的可能的证券。 口其次,无风险资产应当没有市场风险
¾ 根据定义无风险资产具有确定的回报率, 因此: 首先,无风险资产必定是某种具有固定收 益,并且没有任何违约的可能的证券。 其次,无风险资产应当没有市场风险

二、允许无风险贷款下的投资组合 1.投资于一个无风险资产和一个风险资产的情形 >假设风险资产和无风险资产再投资组合中的比例分别为 X,和X2,它们的预期收益率分别为R,和r,标准差分别为 0,和o2,它们之间的协方差为012根据X,和X2的定 义可知X+X2=1,且X和X2>0。根据无风险资产的定 义,有0,和012都等于0。那么, > 该组合的预期收益率为:R=X,R+X2r >组合的标准差为:·。X10
二、允许无风险贷款下的投资组合 允许无风险贷款下的投资组合 1.投资于一个无风险资产和一个风险资产的情形 ¾ 假设风险资产和无风险资产再投资组合中的比例分别为 X1和X2,它们的预期收益率分别为R1和rf,标准差分别为 σ1和σ2,它们之间的协方差为σ12。根据X1和X2的定 义可知X1+ X2=1,且X1和X2>0。根据无风险资产的定 义,有σ1和σ12都等于0。那么, ¾ 该组合的预期收益率为:RP=X1R1+X2rf ¾ 组合的标准差为:σp=X1σ1
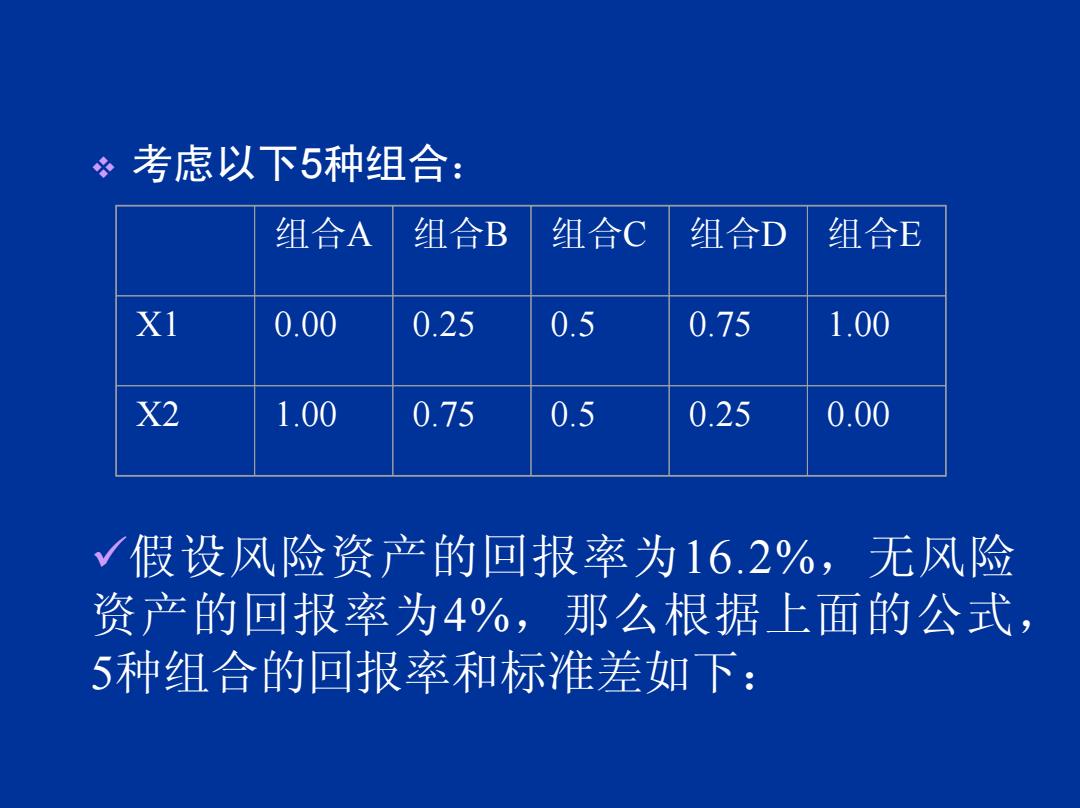
÷考虑以下5种组合: 组合A 组合B 组合C 组合D 组合E XI 0.00 0.25 0.5 0.75 1.00 X2 1.00 0.75 0.5 0.25 0.00 假设风险资产的回报率为16.2%,无风险 资产的回报率为4%,那么根据上面的公式, 5种组合的回报率和标准差如下:
考虑以下5种组合: 组合A 组合B 组合C 组合D 组合E X1 0.00 0.25 0.5 0.75 1.00 X2 1.00 0.75 0.5 0.25 0.00 9假设风险资产的回报率为16.2%,无风险 资产的回报率为4%,那么根据上面的公式, 5种组合的回报率和标准差如下: