
变分原理 设Φ。为任何一个满足体系边界条件的近似基态波函数,则近似基态能 量(能量期待值):W, [Φ。HΦdx Φ。'Φdx B。户体系的Hamilton3算符 Eo 真正的基态能量(Hamilton:算符的最低的能量本征值) 用任何近似基态波函数所计算的能量期待值总是大于真正的基态能量。 设D。=Φ(a,a2,.,am) 为试探波函数(尝试变分函数),其中a,2,a:.a。,是可调参数 则由尝试变分函数计算出来的能量期待值也含有这些可调参数 。=(④平,)/@Φ) =Wo(a,a2,an) 按变分原理,最接近真正基态的是使W极小值,即应满足 形(a,4,.,a)=0i=0.,m oa; 由此方程组解出最佳参数取值,得到在给定的形式之下,最好基态能量近似 值和近似的基态波函数。 31 X.J.WU USTC
变分原理 设 为任何一个满足体系边界条件的近似基态波函数,则近似基态能 量(能量期待值): 0 0 0 0 0 0 0 ˆ E d H d W = H ˆ 体系的Hamilton算符 E0 真正的基态能量 (Hamilton算符的最低的能量本征值) 用任何近似基态波函数所计算的能量期待值总是大于真正的基态能量。 31 X. J. WU @ USTC
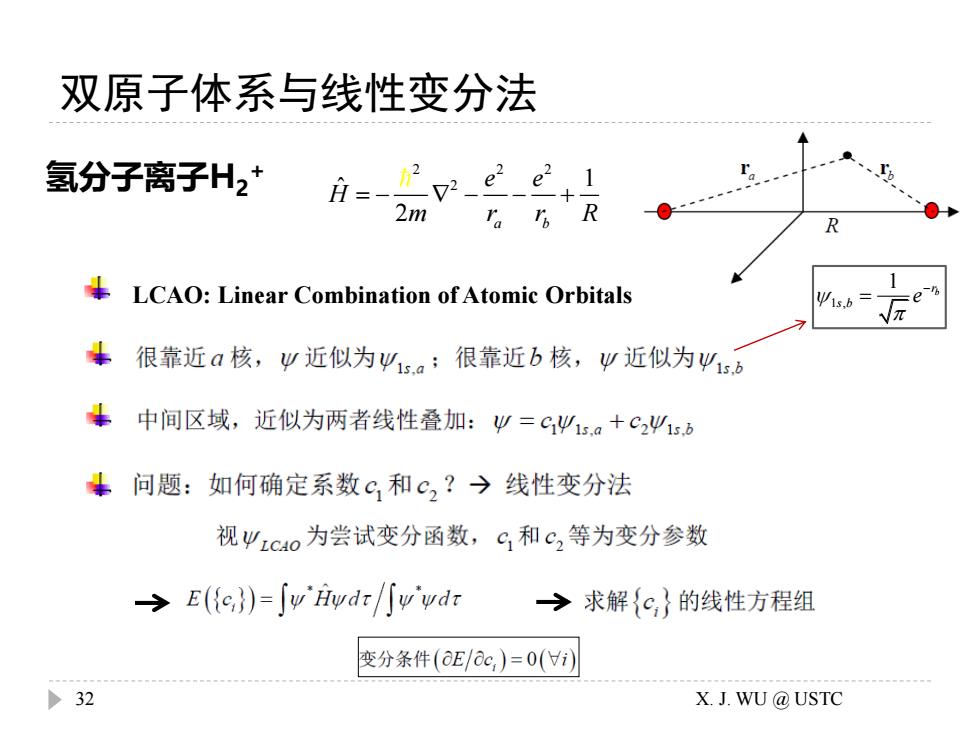
双原子体系与线性变分法 氢分子离子H2+ ǜ= v_e+1 2m R LCAO:Linear Combination of Atomic Orbitals .b =e Nπ 很靠近a核,y近似为y1a;很靠近b核,V近似为1:b 中间区域,近似为两者线性叠加:少=C必1s.a+C21s.b 问题:如何确定系数c和℃2?→线性变分法 视zC4o为尝试变分函数,G和c,等为变分参数 →E({o,)=∫wydr/小wwdr →求解{c,}的线性方程组 变分条件(aE/ac,)=0(i) >32 X.J.WU@USTC
双原子体系与线性变分法 氢分子离子H2 + LCAO: Linear Combination of Atomic Orbitals 1 , 1 b r s b e − = 2 2 2 2 1 ˆ 2 a b e e H m r r R = − − − + 32 X. J. WU @ USTC

线性变分法 1).变分原理: y'Hydr 之Eo w'vdr 变分法: Φ0=Φo(01,02,.,Cm) a,为位置参数 形=(l平,)/@Φ) 0w.(a,a,.,)=0 =W(C1,a2,.,anm) a i=0,.,m 2).线性变分函数 考虑一组满足边界条件的已知函数(基函数),它们线性无关且归一化:{仰,.pn} 尝试变分函数选为这组已知函数的线性组合: 变分参数为组合系数: cj=1.n 这种变分法称为线性变分法。 >33 X.J.WU@USTC
线性变分法 0 ˆ E d H d 1). 变分原理: 变分法 : ( , , , ) 0 = 0 1 2 m ( , , , ) ˆ 0 1 2 0 0 0 0 0 W m W H = = ( 1 , 2 , , ) = 0 o m i W i = 0, ,m αi 为位置参数 2). 线性变分函数 考虑一组满足边界条件的已知函数(基函数),它们线性无关且归一化: 1 n 尝试变分函数选为这组已知函数的线性组合: j n j j c = = 1 变分参数为组合系数: cj j =1,.n 这种变分法称为线性变分法。 33 X. J. WU @ USTC
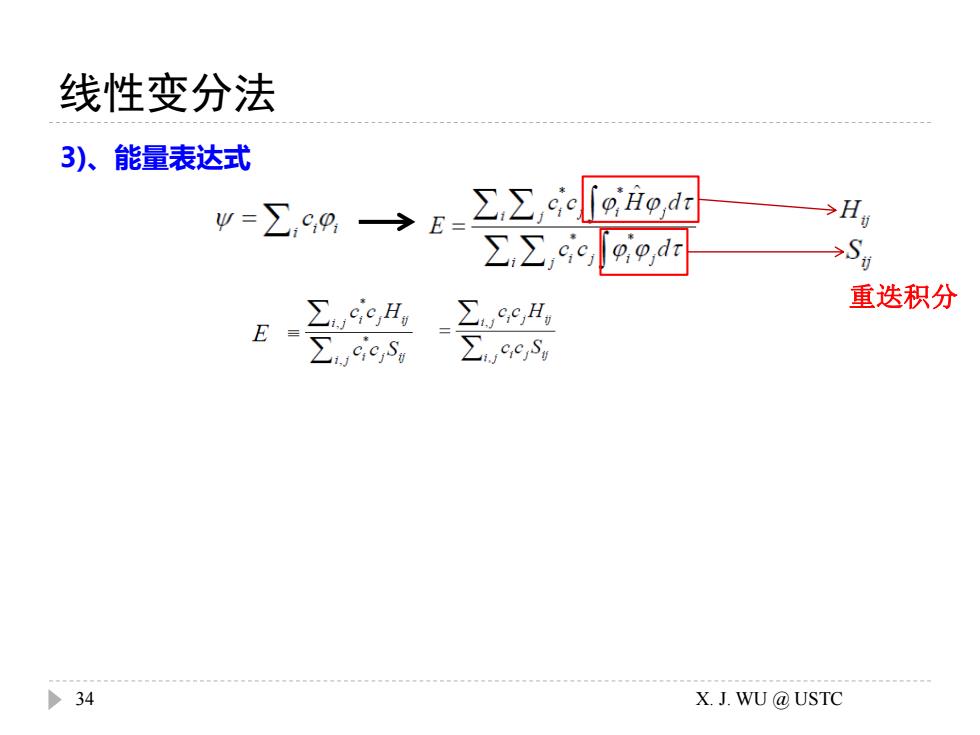
线性变分法 3)、能量表达式 y=∑,c,9>E= ∑,∑,c[9aod →H ∑∑,ic9od →9 9ic,H ∑e,H 重迭积分 ∑wc, 34 X.J.WU@USTC
线性变分法 3)、能量表达式 重迭积分 34 X. J. WU @ USTC

线性变分法 5)、久期方程 久期方程组: ∑L,-,=0 i=l,.,n 将久期方程组写为矩阵形式 H1-eS1.Hn-eSmG 0 : : : (H-S)C=0 Hn-&Sn.Hm-&Sm八Cn】 0 是一个关于个未知数的线性方程组,根据线性代数的知识,有非零解的必要条件 是系数行列式为零,于是有解条件为: detH-sS=0 决定体系的能量 系数方程组 久期方程 ∑,(Ht-ESt)c,=0 H(dk)-ES(O)0 >35 X.J.WU USTC
线性变分法 5)、久期方程 久期方程组: ( − ) = 0 j ij ij j S c i =1, ,n 将久期方程组写为矩阵形式 = − − − − 0 1 0 1 1 11 11 1 1 n n nn nn n n n c c S S S S (Η −S)C = 0 是一个关于n个未知数的线性方程组,根据线性代数的知识,有非零解的必要条件 是系数行列式为零,于是有解条件为: det Η −S = 0 决定体系的能量 系数方程组 久期方程 35 X. J. WU @ USTC