
原子轨道分布图 The Orbitron gallery of atomic orbitals 88 路80
原子轨道分布图 26 X. J. WU @ USTC

自旋 1925年,Uhlenbeck与Goudsmit?提出电子具有一个 intrinsic(built-in)角动量 如果我们将电子看成一个球:-Spin m:= “Spin”不是一个经典效果、旋转模型并不是真实的物理现象 自旋是所有粒子的基本内禀属性之一 电子是费米子,自旋量子数是1/2 ,$,) 具有共同的本征函数,其本征值: 32 ss+1,s=0,2,1,2, S. mh, m=-S,-5+1,.,5-1,S 27 X.J.WU USTC
自旋 1925年,Uhlenbeck与Goudsmit提出电子具有一个 intrinsic(built-in)角动量 如果我们将电子看成一个球:-Spin “Spin” 不是一个经典效果、旋转模型并不是真实的物理现象 自旋是所有粒子的基本内禀属性之一 电子是费米子,自旋量子数是1/2 S ) ˆ S , ˆ ( z 2 具有共同的本征函数,其本征值: 27 X. J. WU @ USTC
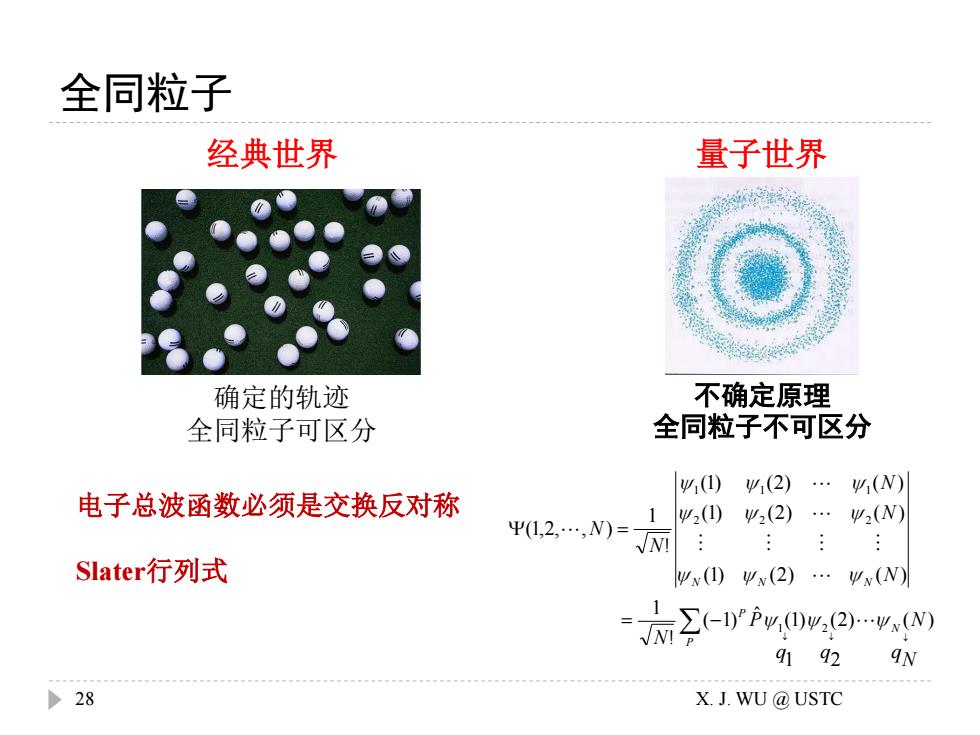
全同粒子 经典世界 量子世界 确定的轨迹 不确定原理 全同粒子可区分 全同粒子不可区分 () 4(2). (N) 电子总波函数必须是交换反对称 1w2(I)42(2).2(N) Y1,2,.,N)= √WI Slater行列式 Wx(I)9x(2) .ww(N) -2-r0-w,M 4192 AN >28 X.J.WU@USTC
全同粒子 经典世界 确定的轨迹 全同粒子可区分 量子世界 不确定原理 全同粒子不可区分 = − = P N P N N N N q N q q P N N N N N N ( ) 2 (2) 1 (1) ˆ ( 1) ! 1 (1) (2) ( ) (1) (2) ( ) (1) (2) ( ) ! 1 (1,2, , ) 1 2 2 2 2 1 1 1 电子总波函数必须是交换反对称 Slater行列式 28 X. J. WU @ USTC

多电子原子与变分法 ()核和电子被视为点粒子。 ()仅仅考虑核与电子、电子与电子之间的静电(库仑)相互作用, 忽略磁相互作用或其它相对论效应。 (ii)假定核不动。(Born-Oppenheim Approximation,l927) Hamilton Operator ㎡g-2+2≥8 -0+刘 h(i)=-1v2_ 2 29 X.J.WU@USTC
多电子原子与变分法 (i) 核和电子被视为点粒子。 (ii)仅仅考虑核与电子、电子与电子之间的静电(库仑)相互作用, 忽略磁相互作用或其它相对论效应。 (iii)假定核不动。(Born-Oppenheim Approximation, 1927) Hamilton Operator = = = = − − + N i N i N i i j i ij i r r Z H 1 1 1 2 1 2 1 ˆ = = + N i N i N j i ij r H h i 1 1 ( ) ˆ ˆ i i r Z h i = − − 2 2 1 ( ) ˆ 29 X. J. WU @ USTC

近似方法 类氢原子模型一零级近似(完全忽略电子间作用) 单电子近似(轨道近似) ,经验屏蔽常数法(Slater轨道) 自洽场(SCF)方法 两电子体系为例 自旋相同,电子1处于(y,),电子2处于(y,a) 总波函数为: ,= a0yap50a2gg,2-g2g,a 1w,a(0),a(2-1 相互作用 月.-x.&auaaawie-9wj0a-wewj e ,② h,y0y2y(2画 aJ- J,称为库仑作用 K”称为交换作用 @(9》e=gn00(w,0n0)dr >30 X.J.WU@USTC
近似方法 类氢原子模型 – 零级近似 (完全忽略电子间作用) 单电子近似(轨道近似) 经验屏蔽常数法(Slater轨道) 自洽场(SCF)方法 30 X. J. WU @ USTC