
1-5-2德布罗意关系式 1924年,受光子学说的启发,年轻的法国物理学家de Broglie提出实物粒子和光一样,具有波粒二象性。如:电 子、质子、中子、原子、分子、离子等。 E=hvλ=h/P=h/mw 例题 子弹,m=2.5×10-2kg,v=300ms1; 电子,m。=9.1X10-31kg,v=5.9X105msl; 波长各是多少?
1-5-2 德布罗意关系式 1924年,受光子学说的启发,年轻的法国物理学家de Broglie提出实物粒子和光一样,具有波粒二象性。如:电 子、质子、中子、原子、分子、离子等。 E=hν = h / P = h / mv 例: 子弹,m = 2.5 × 10-2 kg, v = 300 m·s-1 ; 电子,me = 9.1×10-31kg, v = 5.9×105 m·s-1 ; 波长各是多少?

子弹入=h/(w=6.6×10-34/(2.5×10-2×300) =8.8×1035(m)可忽略,主要表现为粒性。 电子=h/(mw) =6.6×10-34/(9.1×10-31×5.9×105) =12×10-10(m)=1.2nm 可见,高速运动的微粒,其运动规律必然 与宏观物体不同
子弹 = h / (mv) = 6.6×10-34 / (2.5 × 10-2 300) = 8.8 10-35 (m) 可忽略,主要表现为粒性。 电子 = h / (mv) = 6.6×10-34 / (9.1 × 10-31 5.9×105 ) = 12 10-10 (m) = 1.2 nm 可见,高速运动的微粒,其运动规律必然 与宏观物体不同
3年之后,(1927年),C.J.Davisson和L.S.Germer的电子衍 射实验证实了电子运动的波动性一电子衍射图是电子“波” 互相干涉的结果,证实了de Broglie的预言。 1927,美国C.Davisson and L.Germar
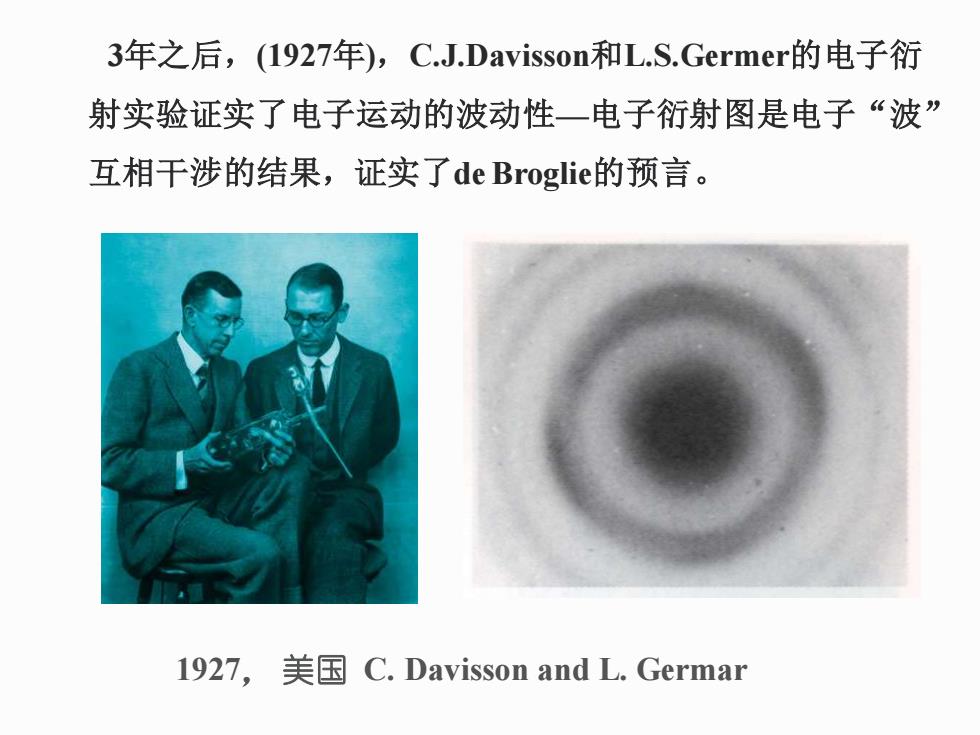
3年之后,(1927年),C.J.Davisson和L.S.Germer的电子衍 射实验证实了电子运动的波动性—电子衍射图是电子“波” 互相干涉的结果,证实了deBroglie的预言。 1927, 美国 C. Davisson and L. Germar

5.2.2不确定原理 1927年W.Heisenberg(海森堡)提出:测量一个 粒子的位置的不确定量么x,与测量该粒子在x方 向的动量分量的不确定量△的乘积,不小于一定 的数值。即:r×△p≥h/2π 或:x×△y≥h/2πm 显然,么x↓,则4p个;4x个,则4p↓; 然而,经典力学认为x和P可以同时很小
5.2.2 不确定原理 1927年W.Heisenberg(海森堡)提出:测量一个 粒子的位置的不确定量 x,与测量该粒子在x方 向的动量分量的不确定量 p的乘积,不小于一定 的数值 。即: x p h / 2 或: x v h / 2m 显然, x ,则 p ; x ,则 p ; 然而,经典力学认为x 和 P 可以同时很小

例题对于m=10克的子弹,它的位置可精确到△x=0.04cm, 兵速度测不准情况为: x×△y≥h/2πm △y≥h/2πmc =2.64×10-28m.s-1 例:微观粒子如电子,m=9.1×10-31kg,运动速度为2.18 ×10m·sl,则电子的运动坐标的测不准情况为: △x≥260pm 所以只有根据“量子力学”,对微观粒子的运动规律, 只能采用“统计”的方法,作出“概率性”的判断
例1: 对于 m = 10 克的子弹,它的位置可精确到x = 0.04 cm, 其速度测不准情况为: x v h / 2m v h / 2mx =2.6410-28m﹒s -1 例: 微观粒子如电子, m = 9.1 10-31 kg, 运动速度为2.18 107m﹒s -1 ,则电子的运动坐标的测不准情况为: △x≥260pm 所以只有根据“量子力学” ,对微观粒子的运动规律, 只能采用“统计”的方法,作出“概率性”的判断