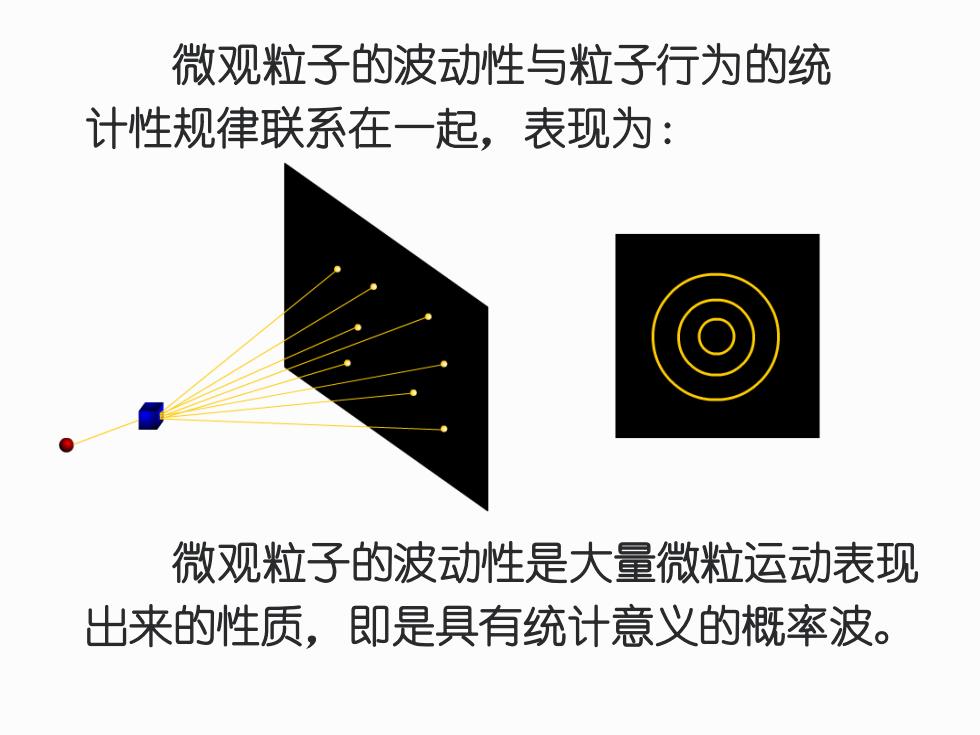
微观粒子的波动性与粒子行为的统 计性规律联系在一起,表现为: 微观粒子的波动性是大量微粒运动表现 出来的性质,即是具有统计意义的概率波
微观粒子的波动性与粒子行为的统 计性规律联系在一起,表现为: 微观粒子的波动性是大量微粒运动表现 出来的性质,即是具有统计意义的概率波

5.3核外电子运动状态的描述 1.电子云 P (wP):概率密度。 电子云是电子在核 外空间概率密度分布的 形象描述。 (小黑点不等同于电子) 在通常状况下氢原子电子云示意图
5.3 核外电子运动状态的描述 1.电子云 ρ (| | 2) :概率密度。 电子云是电子在核 外空间概率密度分布的 形象描述。 (小黑点不等同于电子)

5.3.1薛定谔方程 波函 及 能 势 z 质 zP1靠
8π 2 ( ) 2 2 2 2 2 2 2 EV h m x y z =− − + + x,y,z:空间直角坐标 h:Planck 常数 V:势能 E:能量 :波函数 m:质量 5.3.1 薛定谔方程

薛定谔方程的解 ①方程的解平(化,y,z)非具体数值,而是一函数关系, 是描述核外电子在空间运动的数学函数式(波函 数),即原子轨道; ②有很多数学解平; ③在求合理解的过程中,引入了3个参数,每个特 定解平mm表示电子运动的一稳定状态,借用“轨 道”名称,称乎为原子轨道
①方程的解 (x,y,z)非具体数值,而是一函数关系, 是描述核外电子在空间运动的数学函数式(波函 数),即原子轨道 ; ②有很多数学解Ψ; ③在求合理解的过程中,引入了3个参数,每个特 定解Ψn,l,m表示电子运动的一稳定状态,借用“轨 道”名称,称Ψ为原子轨道。 薛定谔方程的解

1.坐标变换 在解薛定谔方程的过程中,要设法使3个 自变量分离;但在直角坐标系中无法使x、y~ z分开;因此,必须作坐标变换,即:直角坐 标系→球坐标系: 波函数=径向函数×角度函数
1. 坐标变换 在解薛定谔方程的过程中,要设法使3个 自变量分离;但在直角坐标系中无法使x、y、 z分开;因此,必须作坐标变换,即:直角坐 标系→球坐标系: 波函数 = 径向函数 × 角度函数