计算结果: 22 U 品4 8V 电量 Bc/V i/A iclA l/V t=0 4 1 0 t=0, 4 1 I-3 换路瞬间,山z不能跃变,但c公u可以跃变。 2011-11-1 16
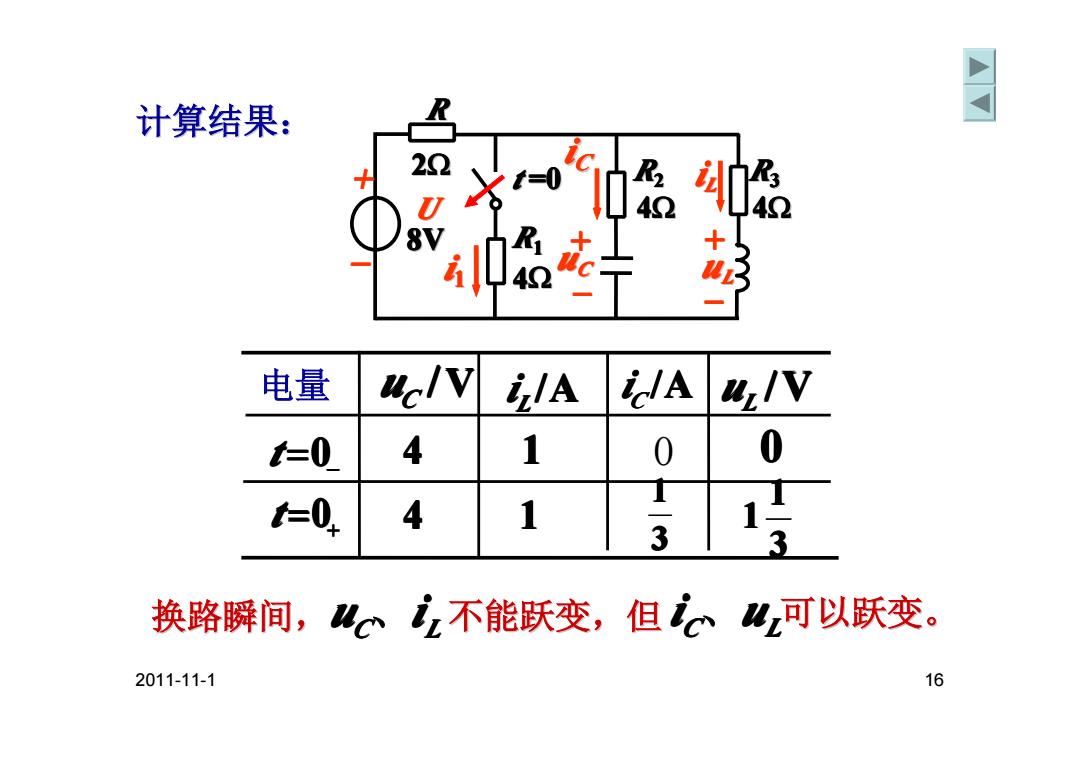
2011-11-1 16 计算结果: 电量 uC / V iL/A iC/A uL /V = + t =0 = − t =0 4 1 1 0 3 1 0 4 3 1 1 换路瞬间, C L u 、i 不能跃变,但 iC、uL可以跃变。 2Ω + _ R R22 R11 U 8V t =0 + + i11 4Ω 4Ω iCC _uCC _uLL iLL R33 4Ω

结论 1.换路瞬间,WGZ不能跃变,但其它电量均可以跃 变。 2.换路前,若储能元件没有储能,换路瞬间(仁0+的等 效电路中),可视电容元件短路,电感元件开路。 3.换路前,若W0-)0,0-≠0,换路瞬间(0,等效 电路中) 电容元件可用一理想电压源替代,其电压为W0+); 电感元件可用一理想电流源替代,其电流为0+)。 2011-11-1 17
2011-11-1 17 结论 1. 换路瞬间,uCC、 iLL不能跃变, 但其它电量均可以跃 但其它电量均可以跃 变。 3. 换路前, 若uCC(0-)≠0,iLL(0-)≠0,换路瞬间 (t=0++等效 电路中) : 电容元件可用一理想电压源替代 电容元件可用一理想电压源替代,其电压为ucc(0 ++); 电感元件可用一理想电流源替代 电感元件可用一理想电流源替代,其电流为iLL(0++)。 2. 换路前, 若储能元件没有储能 若储能元件没有储能, 换路瞬间(t=0++的等 效电路中),可视电容元件短路,电感元件开路。 ,可视电容元件短路,电感元件开路

3.2一阶电路的零输入响应 一阶电路暂态过程的求解方法 一 阶电路 仅含一个储能元件或可等效为一个储能元件的线 性电路,且由一阶微分方程描述,称为一阶线性电 路。 求解方法 1.经典法:根据激励(电源电压或电流),通过求解 电路的微分方程得出电路的响应(电压和电流)。 2.三要素法 初始值 求 稳态值 (三要素) 时间常数 2011-11-1 18
2011-11-1 18 3.2 一阶电路的零输入响应 一阶电路的零输入响应 一阶电路暂态过程的求解方法 一阶电路暂态过程的求解方法 1. 经典法: 根据激励(电源电压或电流 电源电压或电流),通过求解 电路的微分方程得出电路的响应 电路的微分方程得出电路的响应(电压和电流)。 2. 三要素法 初始值 稳态值 时间常数 求 (三要素) 仅含一个储能元件或可等效为一个储能元件的线 仅含一个储能元件或可等效为一个储能元件的线 性电路, 且由一阶微分方程描述,称为一阶线性电 且由一阶微分方程描述,称为一阶线性电 路。 一阶电路 求解方法
3.2.1RC电路的零输入响应 零输入响应:无电源激励,输入 信号为零,仅由电容元件的初 始储能所产生的电路的响应。 实质:RC电路的放电过程 换路前电路已处稳态,(0)=U uc(0_)=U t=0时开关S→1,电容C经电阻R放电 1.电容电压Wc的变化规律(t≥0) (I)列KVL方程hr+4c三O 阶线性常系数 ur iR ic=C duc 齐次微分方程 d/ 代入上式得 RC duc+uc=0 2011-11-1 dt 19
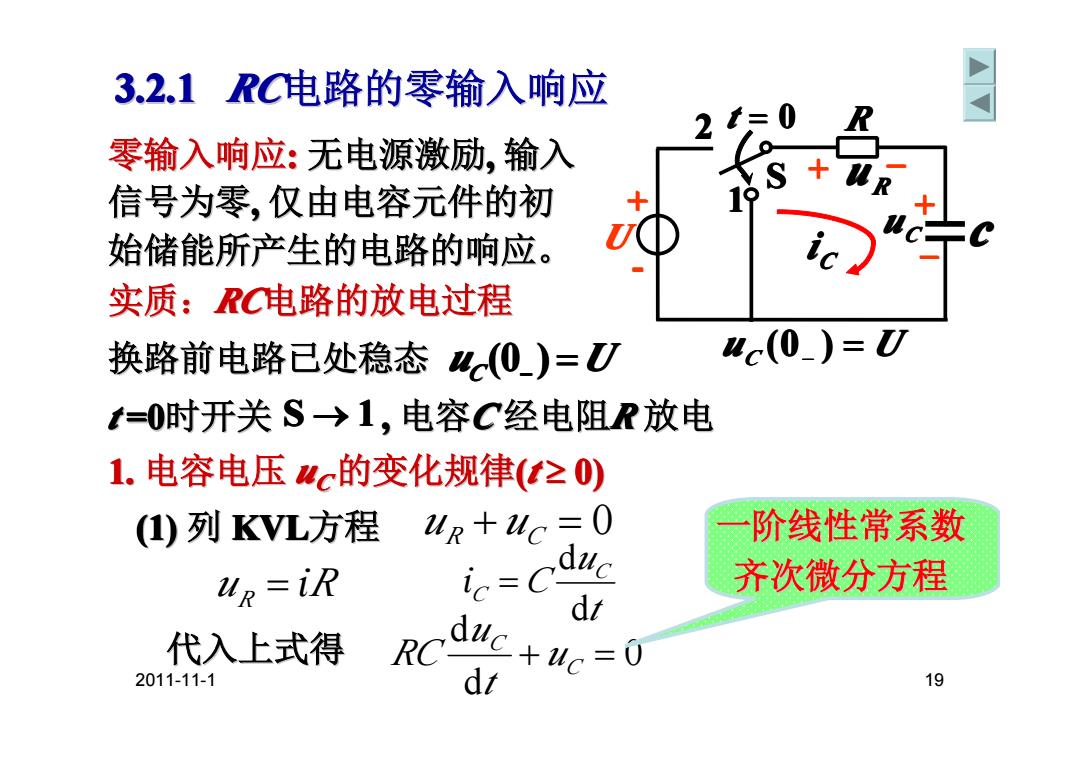
2011-11-1 19 代入上式得 0 d d + C = C u t u RC t u C C C d d u R ι̇ = R =ι̇ 换路前电路已处稳态 换路前电路已处稳态 uC(0− ) =U t =0时开关 S → 1 , 电容C 经电阻R 放电 一阶线性常系数 一阶线性常系数 齐次微分方程 (1) 列 KVL方程 + = 0 u R u C 1. 电容电压 uCC的变化规律(t ≥ 0) 零输入响应: 无电源激励, 输入 信号为零, 仅由电容元件的初 仅由电容元件的初 始储能所产生的电路的响应。 始储能所产生的电路的响应。 实质:RC电路的放电过程 电路的放电过程 3.2.1 3.2.1 3.2.1 3.2.1 3.2.1 3.2.1 3.2.1 3.2.1 RC电路的零输入响应 电路的零输入响应 uC (0 − ) = U + - S R U 2 1 + iC – uC t = 0 u R + – c

(2)解方程:RC dc+c=0通解:c=AeP 特征方程 RCp+1=0p=- RC 齐次微分方程的通解:W2=AeRC 由初始值确定积分常数A 根据换路定则,t=(0,时,4c(0,)=U,可得A=U 3)电容电压Wc的变化规律 uc=UeRc=uc(0,)ett≥0 电容电压Wc从初始值按指数规律衰减, 衰减的快慢由RC决定。 2011-11-1 20
2011-11-1 20 RC p 1 ∴ = − (2) 解方程: 0 d d + C = C u t u RC 特征方程 RCp + 1 = 0 RC t uC A − = e 由初始值确定积分常数 由初始值确定积分常数 A 根据换路定则,t = (0+ )时,uC(0+ ) = U ,可得 A = U RC t u C U − = e 齐次微分方程的通解: 齐次微分方程的通解: 电容电压 uCC从初始值按指数规律衰减, 从初始值按指数规律衰减, 衰减的快慢由RC 决定。 = (0 ) e ≥ 0 − + t C u τ t (3) 电容电压 uCC的变化规律 pt 通解 : uC = Ae