电子科技大学：《导波场论 Field Theory of Guided Waves》课程教学资源（课件讲稿）第二章 规则波导理论（4/5）

导波场论 几种坐标的拉普拉斯算符 拉普拉斯算式，函数的梯度的散度 Vu=V.(V)问题：标量函数经过该运算后是：A、标量；B、矢量 1 H,H3 Ou HH du HH.H 2g.H2 aga"2gs H,ign [H=1 ou 柱坐标拉普拉斯算符Vu=广有 ei 1 a O 12121 V.A= H,H,H 8q a高 4r高u 球坐标拉普拉斯算符号 Ho=p H。=psin V2u= 1 P's sin ap

导 波 场 论  几种坐标的拉普拉斯算符 拉普拉斯算式，函数的梯度的散度   2      u u 2 3 1 3 1 2 1 2 3 1 1 1 2 2 2 3 3 3 1 = + + H H H H u u u H H H H H q H q q H q q H q                                     柱坐标拉普拉斯算符号 2 2 2 2 2 2 1 1 u u u u z                         球坐标拉普拉斯算符号 2 2 2 2 2 1 1 sin + sin + sin sin u u u u                                          问题：标量函数经过该运算后是：A、标量；B、矢量 1 1 z H H H            1 sin H H H               3 1 1 i i i i u u e  H q        2 3 1 1 3 2 1 2 3      1 2 3 1 2 3 1 A H H A H H A H H A e e e + + H H H q q q               

导波场论 >几种坐标的拉普拉斯算符 旋度，三维向量场对某一点附近的微元造成的旋转程度 H,e2 VxA- a a H,H,Hs aq 0q2 0q3 H Ae H,Ae2 H3Aes H,=1 H。=1 H。=1 H,=1 H。=p Ho=p H.=1 H.=1 H。=psin0 直角坐标系 柱坐标系 球坐标系

导 波 场 论  几种坐标的拉普拉斯算符 旋度，三维向量场对某一点附近的微元造成的旋转程度 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 e e e H e H e H e A H H H q q q H A H A H A         1 sin H H H               球坐标系 1 1 z H H H            柱坐标系 1 1 1 x y z H H H         直角坐标系

导波场论 》几种坐标的拉普拉斯算符 几种矢量恒等式 v.Vf=v v×(×A=(.A)-vA V×(7p)=0 梯度是最快方向，不会打旋，为零 也可以有微分算符推导获得 (7×=0 取矢量的旋度时，已经把流出量排除 在外（即没有了流出量部分），再取 散度即为零 也可以有微分算符推导获得

导 波 场 论  几种坐标的拉普拉斯算符 几种矢量恒等式 2    f f     2        A A A        0     A 0 梯度是最快方向，不会打旋，为零 也可以有微分算符推导获得 取矢量的旋度时，已经把流出量排除 在外（即没有了流出量部分），再取 散度即为零 也可以有微分算符推导获得

导波场论 齐次亥姆赫兹方程求解 齐次亥姆赫兹方程 V2E+k2E=0 Vp+(k2+y2)b=0 72五+k2五=0 直坐标系，X、Y、乙，三个均有通解形式： U+a.U+b.U=0 U-Ce*+Ceix U"+b.U=0 U-Ce+Ce=e.(Csin(Bx)+C:cos(Bx)) 一c05(X) —c05《X) 欧拉公式 e=cosx+j.sinx

导 波 场 论 齐次亥姆赫兹方程 2 2 2 2 0 0 k k          E E H H 直坐标系，X、Y、Z，三个均有通解形式： 2 2 2 ( ) 0 t        k " ' U +a U +b U=0   1 2 U= 1 2 x x C e C e    " U +b U=0  U= 1 2 x x C e C e      1 2 sin( x) cos( x) x e C C       cos sin jx e x j x    欧拉公式  齐次亥姆赫兹方程求解

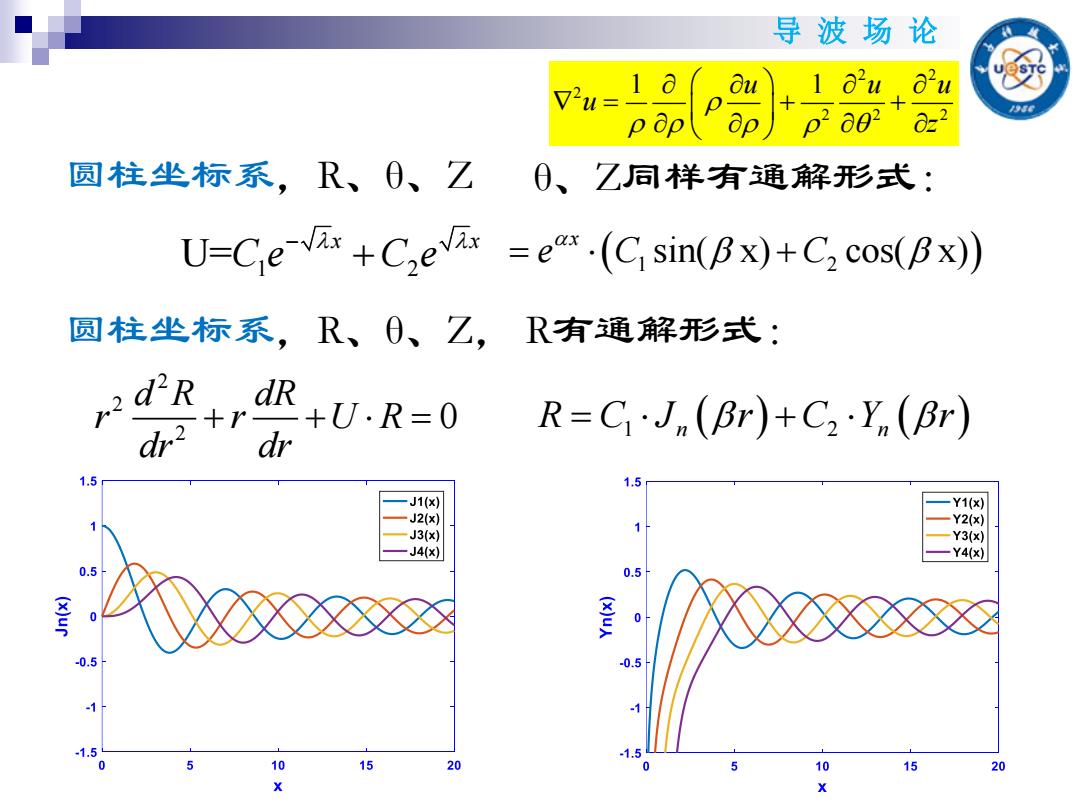
导波场论 pp ap a 20z2 圆柱坐标系，R、0、乙 0、乙同样有通解形式： U=Cex+Cevx =e(C.sin(Bx)+C2cos(Bx)) 圆柱坐标系，R、0、乙， R有通解形式： r2diR dR +r +U.R=0 dr2 R=CJ (Br)+C2Y (Br) dr 1.5 1.5 J1(x) Y1(x) J2(x) Y2(x) J3(x) Y3(x) J4(x) Y4(x) 0.5 0.5 0 0.5 0.5 -1 -1.5 1.5 0 10 15 20 10 15 % X

导 波 场 论 圆柱坐标系，R、θ、Z 2 2 2 0 d R dR r r U R dr dr     圆柱坐标系，R、θ、Z， R有通解形式： U= 1 2 x x C e C e      1 2 sin( x) cos( x) x e C C       R C J r C Y r     1 2 n n      2 2 2 2 2 2 1 1 u u u u z                         θ、Z同样有通解形式：