
二、课程简介 《高等数学(1)》是现代高等教奋阶段的一门其础学科。是经济统计学专业太科生的数 学基础课,是必修的重要理论基础课程。通过本课程的学习,要使学生比较系统地获得函数 极限、 定积分 反常积分、微 分方程等方面的概念 基本理论和基本运算技 逐步培养学生抽象概括问题的能力、逻辑推理能力、空间想象能力和比较熟练的运算能力 从而使学生掌握相应的数学方法并培养学生运用掌握的方法尝试解决实际问题,为学习后续 课程奠定必要的数学基础。 三、课程目标及对毕业要求(及其指标点)的支撑 公共类课程《高等数学(1)》的课程目标 序号 课程目标 元函数极限:理解极限的描述性定义及性质,理解无穷小与无穷大的概 1 握利用等价无穷 、两个重要极限求极限 、洛必达法则等多种方法求极限 理 函数的连续性、掌握并会判断间断点的类型。在解决实际问题中能够通过求极限 将离散模型转化成连续模型。 一元函数导数:理解导数的概念.熟记常见函数(幂、指、对、三角、反三角) 的导数结果;掌握链式求导法则及隐函数、参数方程确定函数的导数:理解函数 2 的微分,并会计算一元函数的 会解 阶数 在所学专业内容中表 示的实际意义,并能建立数学模型、解释数学模型中导数项所表达的含义。 中值定理及导数应用:理解微分中值定理:堂樱判断函数的单调性。理解曲线的 3 凹几性及相¥别方法 会计算拐点,掌握一元函数极值、最值的求法。 会将求 极值、最值的方法与所学专业结合,计算专业内容中涉及的极值、最值问题。 一元函数积分及应用:理解不定积分和定积分的概念及性质,掌握不定积分与定 积分的常见计算方法(两类换元法。分部积分法】,会计算简单的有理积分 握利用定积分计算平面图形面积与旋转体体积 理解反常积分的定义、掌握常见 反常积分的计算(包括计算无穷区间上面积、旋转体的体积)。理解积分在本专 业解决实际问题中的应用.并会解释相关的积分项含义。 常微分方程:理解微分方程的定义,掌握一阶微分方程(可分离变量法、常数变 系 线性微分方程的求解方法。理解微分方程解的 5 掌握二阶 于右端项简单的二阶非齐次方程,掌握特解的设法。 理解所学专业内容中涉及的 微分方程,并会运用所学方法求解微分方程。 四、教学内容教学环节及进度安排 序号 教学内容/教学环节 学生学习预期成果 授课方式支撑课 及学时 程目标 主要教学内容:1数列与函数的极限 理解极限的描沭件定 极限的性质。 2无穷小的概念与性质 义及性质 理解无究 无穷大的概念,无穷小和无穷大的关系 小与无穷大的概念 1 无穷小比较。3极限的运算法则.4极限 12 堂握利用等价无穷 存在准则两个重要极限。5函数连续 小、两个重要极限求 的概念,函数的间断点,初等函数的连 极限 理解函数的连
14 二、课程简介 《高等数学(1)》是现代高等教育阶段的一门基础学科,是经济统计学专业本科生的数 学基础课,是必修的重要理论基础课程。通过本课程的学习,要使学生比较系统地获得函数、 极限、不定积分、定积分、反常积分、微分方程等方面的概念、基本理论和基本运算技能。 逐步培养学生抽象概括问题的能力、逻辑推理能力、空间想象能力和比较熟练的运算能力。 从而使学生掌握相应的数学方法并培养学生运用掌握的方法尝试解决实际问题,为学习后续 课程奠定必要的数学基础。 三、课程目标及对毕业要求(及其指标点)的支撑 公共类课程《高等数学(1)》的课程目标 序号 课程目标 1 一元函数极限:理解极限的描述性定义及性质,理解无穷小与无穷大的概念,掌 握利用等价无穷小、两个重要极限求极限、洛必达法则等多种方法求极限;理解 函数的连续性、掌握并会判断间断点的类型。在解决实际问题中能够通过求极限 将离散模型转化成连续模型。 2 一元函数导数:理解导数的概念,熟记常见函数(幂、指、对、三角、反三角) 的导数结果;掌握链式求导法则及隐函数、参数方程确定函数的导数;理解函数 的微分,并会计算一元函数的微分。会解释一阶、二阶导数在所学专业内容中表 示的实际意义,并能建立数学模型、解释数学模型中导数项所表达的含义。 3 中值定理及导数应用:理解微分中值定理;掌握判断函数的单调性,理解曲线的 凹凸性及相关判别方法,会计算拐点;掌握一元函数极值、最值的求法。会将求 极值、最值的方法与所学专业结合,计算专业内容中涉及的极值、最值问题。 4 一元函数积分及应用:理解不定积分和定积分的概念及性质,掌握不定积分与定 积分的常见计算方法(两类换元法、分部积分法),会计算简单的有理积分,掌 握利用定积分计算平面图形面积与旋转体体积,理解反常积分的定义、掌握常见 反常积分的计算(包括计算无穷区间上面积、旋转体的体积)。理解积分在本专 业解决实际问题中的应用,并会解释相关的积分项含义。 5 常微分方程:理解微分方程的定义,掌握一阶微分方程(可分离变量法、常数变 易法),掌握二阶常系数线性微分方程的求解方法,理解微分方程解的结构,对 于右端项简单的二阶非齐次方程,掌握特解的设法。理解所学专业内容中涉及的 微分方程,并会运用所学方法求解微分方程。 四、教学内容/教学环节及进度安排 序号 教学内容/教学环节 学生学习预期成果 授课方式 及学时 支撑课 程目标 1 主要教学内容:1.数列与函数的极限, 极限的性质。2 无穷小的概念与性质, 无穷大的概念,无穷小和无穷大的关系, 无穷小比较。3 极限的运算法则.4 极限 存在准则,两个重要极限。5 函数连续 的概念,函数的间断点,初等函数的连 理解极限的描述性定 义及性质,理解无穷 小与无穷大的概念, 掌握利用等价无穷 小、两个重要极限求 极限;理解函数的连 12 1 上海电机学院商学院

序号 教学内容/教学环节 学生学习预期成果 授课方式支撑课 及学时程目标 续性。 续性、掌握并会判断 教学重点、难点: 间新点的类型。 极限的定义、无穷小的比较、利用两个 重要极限求极限、函数连续的定义、 断点类型的判断 思政融合点1:(极限部分】 圆周率的计算(代表人物刘徽、祖冲之) 中国士代数学宴刘微在割圆未中提出 的”割之弥细,所失弥少,割之又制以 于不可割,则与圆合体而无所失矣“,这 可视为中国古代极限观念的佳作。让学 生体会中国古代数学的限苦探索历 程,提升对中华文化的认同,增强文化 自信。 思政融合点2:(无穷小部分) 中国古代哲学家墨子说:“穷,或不容尺 有穷:莫不容尺无穷也,”墨子分析 穷”“无穷”的定义墨子认为宇宙无边无 际,时间无始无终,含有无穷大的概念 培养学生体会事物间的相互转化。对 统一的辩证关系。 主要教学内容: 1导数的定义,导数的儿何意义,函敬 可导与连续的关系。2函数的和、差的 求导法则,函数的积、商的求导法则, 反函数的求导法则、复合函数的求导法 理解导数的概念,熟 则,高阶导数的运算。3隐函数及其求 记常见函数(幂函数 导法,参数方程所确定的函数的求导法 指数函数、对数函数 三角函数、反三角函 4微分的概念,微分的几何意义,微分 数)的导数结果:堂 课堂讲授 本公式与运算法则 握链式求导法则及隐 10 教学重点、难点:导数的定义、函数积 函数、参数方程确定 商求导、复合函数链式求导法则、隐承 函数的导数;理解函 数及参数方程求二阶导数 一元函数筒 数的微分,并会计算 分的定义及意义。 元函数的微分 思政融合点: “失之毫厘,谬以干里“培养学生形成严 谨的作风,让学生在学习生活中,要从 源头上消除偏差,防止造成失之毫厘, 谬以千里的后果
15 序号 教学内容/教学环节 学生学习预期成果 授课方式 及学时 支撑课 程目标 续性。 教学重点、难点: 极限的定义、无穷小的比较、利用两个 重要极限求极限、函数连续的定义、间 断点类型的判断 思政融合点 1:(极限部分) 圆周率的计算(代表人物刘徽、祖冲之) 中国古代数学家 刘徽在“割圆术”中提出 的"割之弥细,所失弥少,割之又割以至 于不可割,则与圆合体而无所失矣",这 可视为中国古代极限观念的佳作。让学 生体会中国古代数学家的艰苦探索历 程,提升对中华文化的认同,增强文化 自信。 思政融合点 2:(无穷小部分) 中国古代哲学家墨子说:“窮,或不容尺 有穷;莫不容尺无穷也.”墨子分析了“有 穷”“无穷”的定义.墨子认为宇宙无边无 际,时间无始无终,含有无穷大的概念. 培养学生体会事物间的相互转化,对立 统一的辩证关系。 续性、掌握并会判断 间断点的类型。 2 主要教学内容: 1 导数的定义,导数的几何意义,函数 可导与连续的关系。2 函数的和、差的 求导法则,函数的积、商的求导法则, 反函数的求导法则,复合函数的求导法 则,高阶导数的运算。3 隐函数及其求 导法,参数方程所确定的函数的求导法 4 微分的概念,微分的几何意义,微分 基本公式与运算法则。 教学重点、难点:导数的定义、函数积、 商求导、复合函数链式求导法则、隐函 数及参数方程求二阶导数、一元函数微 分的定义及意义。 思政融合点: “失之毫厘,谬以千里”.培养学生形成严 谨的作风,让学生在学习生活中,要从 源头上消除偏差,防止造成失之毫厘, 谬以千里的后果。 理解导数的概念,熟 记常见函数(幂函数、 指数函数、对数函数、 三角函数、反三角函 数)的导数结果;掌 握链式求导法则及隐 函数、参数方程确定 函数的导数;理解函 数的微分,并会计算 一元函数的微分。 课堂讲授 10 2 上海电机学院商学院
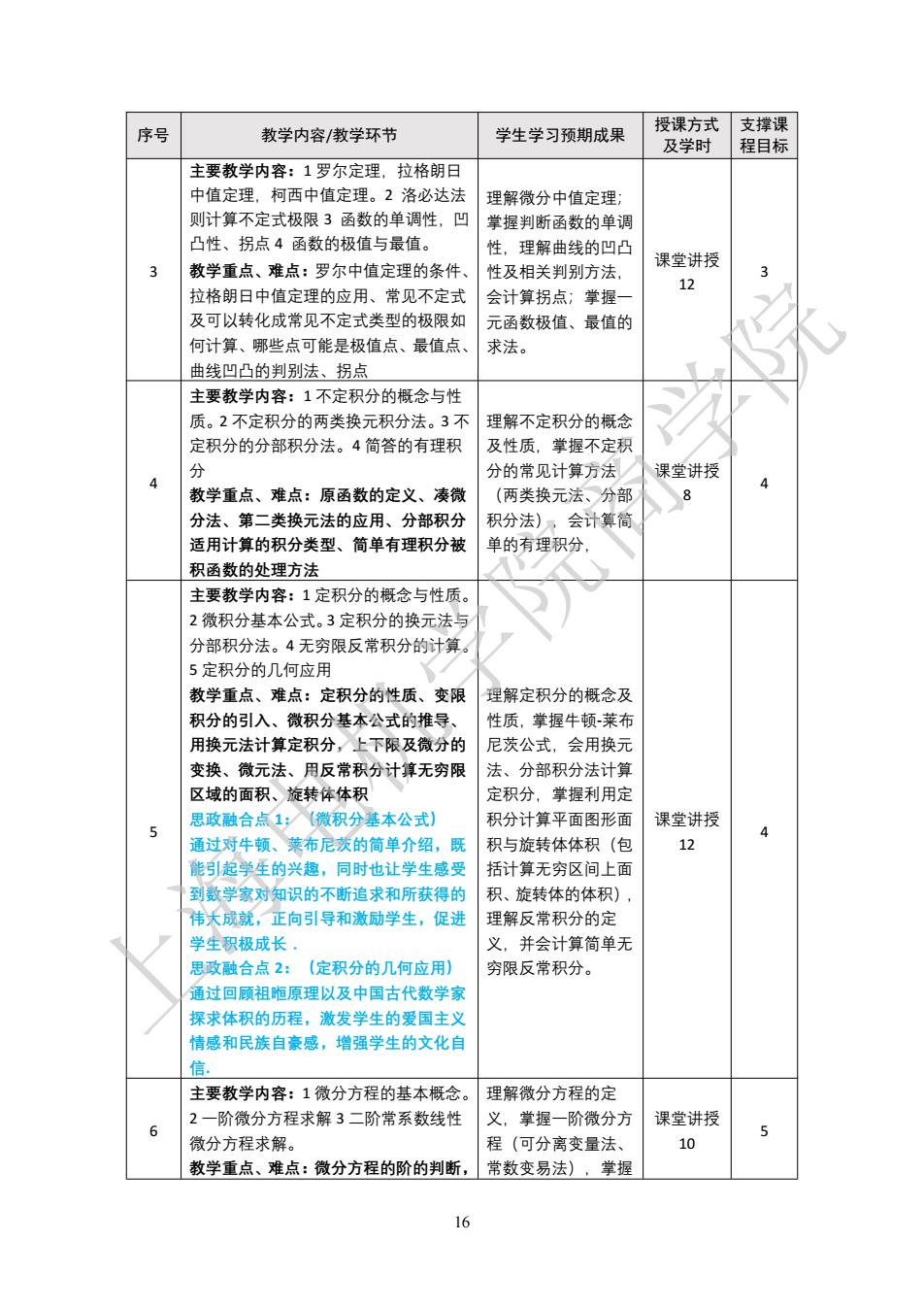
序号 教学内容/敷学环节 学生学习预期成果 授课方式支撑课 及学时 程目标 主要教学内容:1罗尔定理,拉格朗日 中值定理,柯西中值定理。2洛必达法 理解微分中值定理 则计 不定式极限3函数的单调性,凹 掌握判断函数的单调 凸性、拐点4函数的极值与最值 性,理解曲线的凹凸 3 教学重点、难点:罗尔中值定理的条件 性及相关别方法 课堂讲授 拉格朗日中值定理的应用、常见不定 会计算拐点:掌握 及可以转化成常见不定式类型的极限如 元函数极值、最值的 何计算、哪些点可能是极值点、最值点 求法。 曲线凹凸的判别法、拐点 主要教 内容: 1不定积分的概念与性 质。2不定积分的两类换元积分法。3不 理解不定积分的概念 定积分的分部积分法。4简答的有理积 及性质章握不定利 分的常见计算方法 课堂讲授 教学重点、难点:原函数的定义、凑微 (两类换元法 分法、第二类换元法的应用、分部积分 积分法)会计算简 适用计算的积分类型、简单有理积分被 单的有理积分, 积函数的处理方法 主要教学内容: 1定积分的概念与性质 2微积分基本公式。3定积分的换元法 分部积分法。4无穷限反常积分的计算 5定积分的几何应用 教学重点、难点:定积分的性质、变限 理解定积分的概念及 积分的引入、微积分基本公式的推导、 性质,掌挥牛顿莱有 用换元法计算定积分,上下限及微分的 尼茨公式.会用换元 变换、微元法、用反常积分计算无穷限 法、分部积分法计算 区的面知桂休休 定积分 掌握利用定 思政融合点1:(微积分基本公式) 积分计算平面图形面 5 课堂讲授 通过对牛顿、莱布尼发的简单介绍,既 积与旋转体体积(包 12 能引起学生的兴趣,同时也让学生感受 括计算无穷区间上面 到数学家对知识的不断追求和所获得的 积 、旋转体的体 伟天成就,正向引导和激励学生,促进 理解反常积分的定 学生积极成长, 义,并会计算简单无 思政融合点2:(定积分的几何应用) 穷限反常积分。 通过回顾祖原理以及中国古代数学家 探求体积的历程,激发学生的爱国主义 情感和民族自豪感,增强学生的文化自 主要教学内容:1微分方程的基本概念 里解微分方程的 2一阶微分方程求解3二阶常系数线性 义, 掌握一阶微分方 课堂讲授 6 微分方程求解。 程(可分离变量法 10 教学重点、难点:微分方程的阶的判断, 常数变易法),掌握 6
16 序号 教学内容/教学环节 学生学习预期成果 授课方式 及学时 支撑课 程目标 3 主要教学内容:1 罗尔定理,拉格朗日 中值定理,柯西中值定理。2 洛必达法 则计算不定式极限 3 函数的单调性,凹 凸性、拐点 4 函数的极值与最值。 教学重点、难点:罗尔中值定理的条件、 拉格朗日中值定理的应用、常见不定式 及可以转化成常见不定式类型的极限如 何计算、哪些点可能是极值点、最值点、 曲线凹凸的判别法、拐点 理解微分中值定理; 掌握判断函数的单调 性,理解曲线的凹凸 性及相关判别方法, 会计算拐点;掌握一 元函数极值、最值的 求法。 课堂讲授 12 3 4 主要教学内容:1 不定积分的概念与性 质。2 不定积分的两类换元积分法。3 不 定积分的分部积分法。4 简答的有理积 分 教学重点、难点:原函数的定义、凑微 分法、第二类换元法的应用、分部积分 适用计算的积分类型、简单有理积分被 积函数的处理方法 理解不定积分的概念 及性质,掌握不定积 分的常见计算方法 (两类换元法、分部 积分法),会计算简 单的有理积分, 课堂讲授 8 4 5 主要教学内容:1 定积分的概念与性质。 2 微积分基本公式。3 定积分的换元法与 分部积分法。4 无穷限反常积分的计算。 5 定积分的几何应用 教学重点、难点:定积分的性质、变限 积分的引入、微积分基本公式的推导、 用换元法计算定积分,上下限及微分的 变换、微元法、用反常积分计算无穷限 区域的面积、旋转体体积 思政融合点 1:(微积分基本公式) 通过对牛顿、莱布尼茨的简单介绍,既 能引起学生的兴趣,同时也让学生感受 到数学家对知识的不断追求和所获得的 伟大成就,正向引导和激励学生,促进 学生积极成长. 思政融合点 2:(定积分的几何应用) 通过回顾祖暅原理以及中国古代数学家 探求体积的历程,激发学生的爱国主义 情感和民族自豪感,增强学生的文化自 信. 理解定积分的概念及 性质,掌握牛顿-莱布 尼茨公式,会用换元 法、分部积分法计算 定积分,掌握利用定 积分计算平面图形面 积与旋转体体积(包 括计算无穷区间上面 积、旋转体的体积), 理解反常积分的定 义,并会计算简单无 穷限反常积分。 课堂讲授 12 4 6 主要教学内容:1 微分方程的基本概念。 2 一阶微分方程求解 3 二阶常系数线性 微分方程求解。 教学重点、难点:微分方程的阶的判断, 理解微分方程的定 义,掌握一阶微分方 程(可分离变量法、 常数变易法),掌握 课堂讲授 10 5 上海电机学院商学院
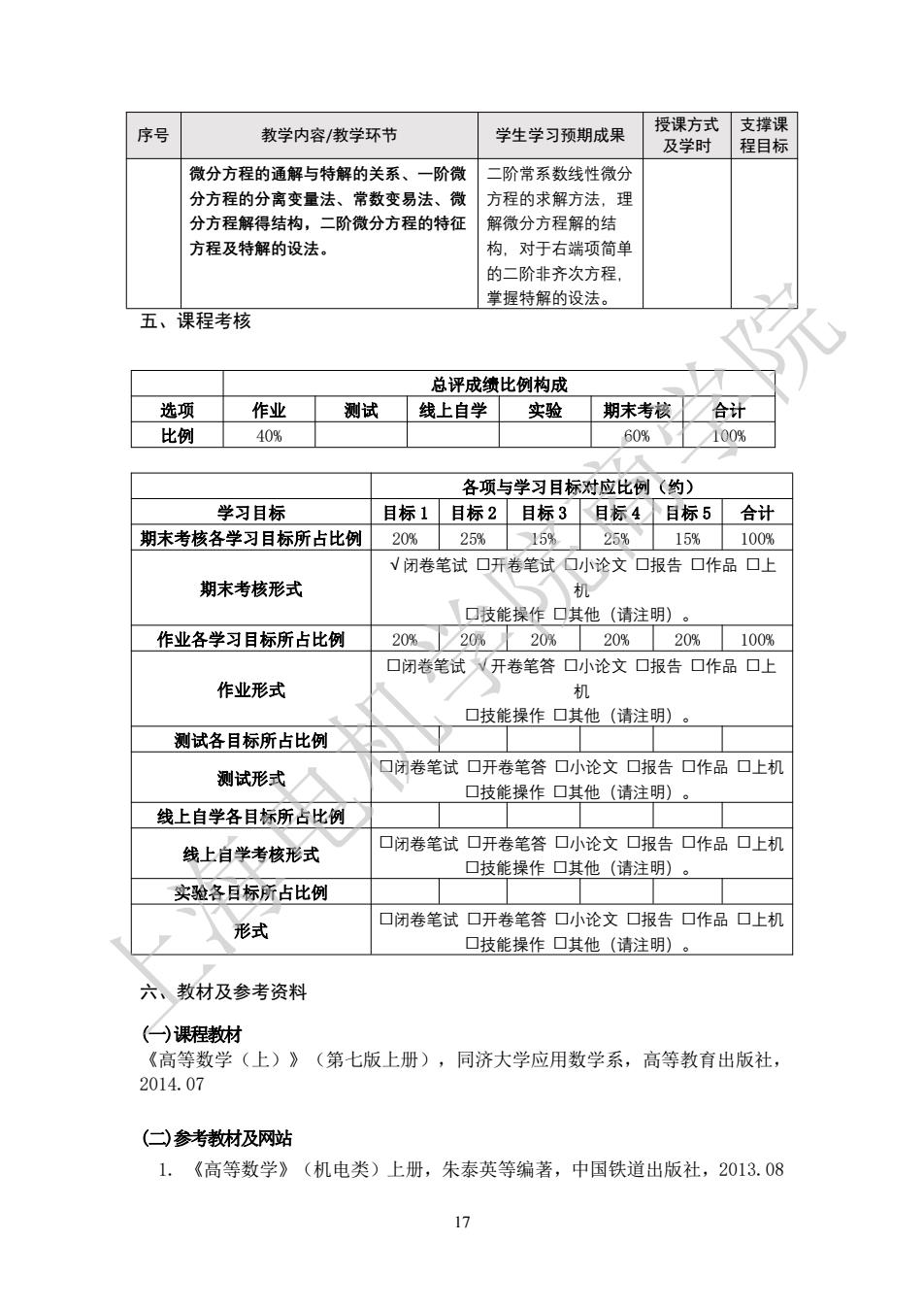
序号 教学内容/教学环节 学生学习预期成果 授课方式支撑课 及学时程目标 微分方程的通解与特解的关系、 阶微 二阶带系数线性微分 分方程的分离变量法、常数变易法、微 方程的求解方法,理 分方程解得结构,二阶微分方程的特征解微分方程解的结 方程及特解的设法。 的二阶非齐次方程 掌握特解的设法。 五、课程考核 总评成绩比例构成 选项 作业 测试 线上自学实验 期末考核合计 比例 40% 60%100序 各项与学习目标对应比例(的) 学习目标 目标1目标2目标3目标4下目标5合计 期末考核各学习目标所占比例 20% 25 15% 25% 15% 100% √闭卷笔试口开卷笔试口小论文口报告口作品口上 期末考核形式 机 【口技能操作口其他(请注明) 作业各学习目标所占比例 20%/20%20% 20% 20%100% 口闭卷笔试√开卷笔答口小论文口报告口作品口上 作业形式 ☐技能操作口其他(请注明)】 测试各目标所占比例 测试形式 口闭卷笔试口开卷笔答口小论文口报告口作品口上机 口技能操作口其他(请注明) 线上自学各目标所占比例 线上自学考核形式 口闭卷笔试口开卷笔答口小论文口报告口作品口上机 口技能操作▣其他(请注明) 实验各目标所占比例 形式 口闭卷笔试口开卷笔答口小论文口报告口作品口上机 口技能操作口其他(请注明)。 六、教材及参考资料 (一)课程教村 《高等数学(上)》(第七版上册),同济大学应用数学系,高等教育出版社 2014.07 (仁)参考教村及网站 1.《高等数学》(机电类)上册,朱泰英等编著,中国铁道出版社,2013.08 17
17 序号 教学内容/教学环节 学生学习预期成果 授课方式 及学时 支撑课 程目标 微分方程的通解与特解的关系、一阶微 分方程的分离变量法、常数变易法、微 分方程解得结构,二阶微分方程的特征 方程及特解的设法。 二阶常系数线性微分 方程的求解方法,理 解微分方程解的结 构,对于右端项简单 的二阶非齐次方程, 掌握特解的设法。 五、课程考核 总评成绩比例构成 选项 作业 测试 线上自学 实验 期末考核 合计 比例 40% 60% 100% 各项与学习目标对应比例(约) 学习目标 目标 1 目标 2 目标 3 目标 4 目标 5 合计 期末考核各学习目标所占比例 20% 25% 15% 25% 15% 100% 期末考核形式 √闭卷笔试 开卷笔试 小论文 报告 作品 上 机 技能操作 其他(请注明)。 作业各学习目标所占比例 20% 20% 20% 20% 20% 100% 作业形式 闭卷笔试 √开卷笔答 小论文 报告 作品 上 机 技能操作 其他(请注明)。 测试各目标所占比例 测试形式 闭卷笔试 开卷笔答 小论文 报告 作品 上机 技能操作 其他(请注明)。 线上自学各目标所占比例 线上自学考核形式 闭卷笔试 开卷笔答 小论文 报告 作品 上机 技能操作 其他(请注明)。 实验各目标所占比例 形式 闭卷笔试 开卷笔答 小论文 报告 作品 上机 技能操作 其他(请注明)。 六、教材及参考资料 (一)课程教材 《高等数学(上)》(第七版上册),同济大学应用数学系,高等教育出版社, 2014.07 (二)参考教材及网站 1. 《高等数学》(机电类)上册,朱泰英等编著,中国铁道出版社,2013.08 上海电机学院商学院

2.《高等数学》,曾庆柏主编,中国人民大学出版社,2010.09 3.《高等数学习题分析与解答》(机电类),朱泰英等编著,中国铁道出版社 201508 4.《托马斯微积分》(第十版),叶其孝等译,高等教育出版社,2016.8 上海电机学院商学院 编写人:感建明审核人:郭鹏一 审批人:王玉芬 _市批日期: 2022
18 2. 《高等数学》,曾庆柏主编,中国人民大学出版社,2010.09 3. 《高等数学习题分析与解答》(机电类),朱泰英等编著,中国铁道出版社, 2015.08 4. 《托马斯微积分》(第十版),叶其孝等译,高等教育出版社,2016.8 编写人: 戚建明 审核人: 郭鹏 审批人: 王玉芬 审批日期: 2022.1 上海电机学院商学院