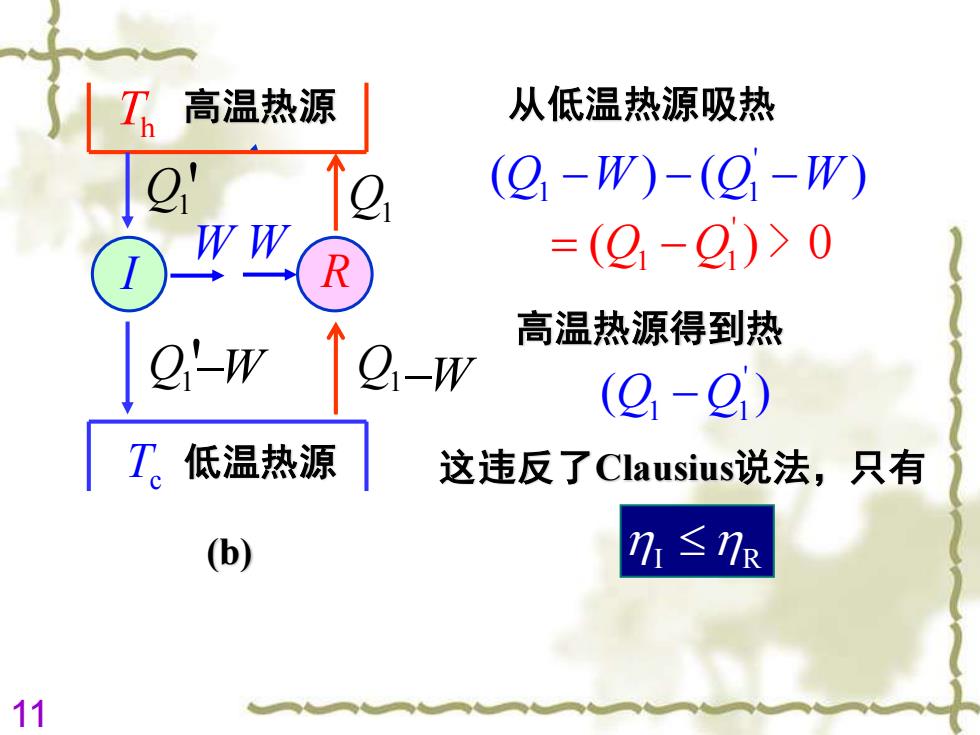
高温热源 从低温热源吸热 (g,-W)-(Q-W) WW R =(9-9)>0 高温热源得到热 2-w (9-2) T低温热源 这违反了Clausiusi说法,只有 (b) 71≤7R 11
11 Th 高温热源 Tc 低温热源 Q1 W Q1 ' W Q1 '−W Q1−W I R (b) ' 1 1 ( ) ( ) Q W Q W − − − ' 1 1 = − ( ) 0 Q Q > 从低温热源吸热 I R 高温热源得到热 ' 1 1 ( ) Q Q− 这违反了Clausius说法,只有

Carnot定理: 所有工作于同温热源和同温冷源之间的热机,其 效率都不能超过可逆机,即可逆机的效率最大。 Carnot定理推论: 所有工作于同温热源与同温冷源之间的可逆热机, 其热机效率都相等,即与热机的工作物质无关。 Carnot定理的意义: (1)i 引入了一个不等号1≤,原则上解决了 化学反应的方向问题; (2)原则上解决了热机效率的极限值问题。 12
12 Carnot定理: Carnot定理推论: Carnot定理的意义: (2)原则上解决了热机效率的极限值问题。 (1)引入了一个不等号 ,原则上解决了 化学反应的方向问题; I R 所有工作于同温热源和同温冷源之间的热机,其 效率都不能超过可逆机,即可逆机的效率最大。 所有工作于同温热源与同温冷源之间的可逆热机, 其热机效率都相等, 即与热机的工作物质无关

§3.4熵的概念 从Carnot循环得到的结论: 即Carnot循环中,热效应与温度商值的加和等于零 0+ h=0 Te Th 对于任意的可逆循环,都可以分解为若干个小 Carnot循环。 13
13 §3.4 熵的概念 从Carnot循环得到的结论: c h c h 0 Q Q T T + = 对于任意的可逆循环,都可以分解为若干个小 Carnot循环。 即Carnot循环中,热效应与温度商值的加和等于零

任意可逆循环的热温商 证:任意可逆循环可以被许多绝热可逆线和定温可逆 线分割成许多小卡诺循环: 而每个小卡诺循环的热温商之和为零 :d0+62 2=0 相邻两个小卡诺循环的绝热 可逆线抵消: 当折线段趋于无穷小时: z婴=f,%· 14
14 p V 证:任意可逆循环可以被许多绝热可逆线和定温可逆 线分割成许多小卡诺循环: i i Q Q Q T T T + + = = 1 2 1 2 0 i i Q T = 相邻两个小卡诺循环的绝热 可逆线抵消: 而每个小卡诺循环的热温商之和为零 当折线段趋于无穷小时: 任意可逆循环的热温商 0 δ R = T Q
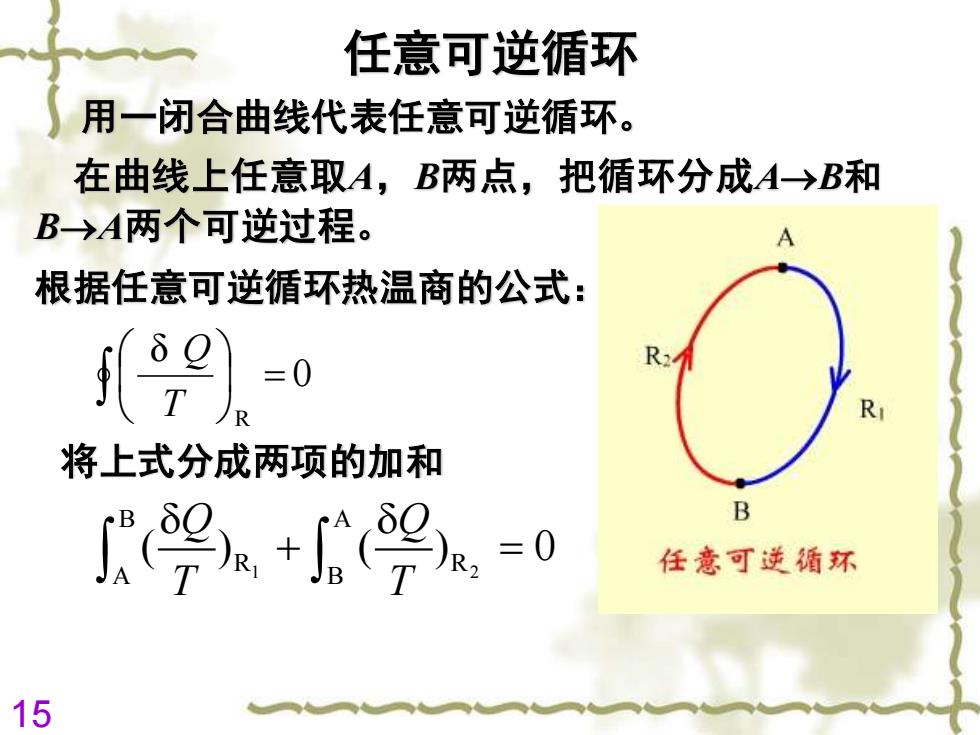
任意可逆循环 用一闭合曲线代表任意可逆循环。 在曲线上任意取A,B两点,把循环分成A→B和 B→A两个可逆过程。 根据任意可逆循环热温商的公式: )-0 R2 R 将上式分成两项的加和 9a+9.=0 B 任意可逆循环 15
15 任意可逆循环 用一闭合曲线代表任意可逆循环。 1 2 B A R R A B ( ) ( ) 0 Q Q T T + = 将上式分成两项的加和 在曲线上任意取A,B两点,把循环分成A→B和 B→A两个可逆过程。 根据任意可逆循环热温商的公式: 0 δ R = T Q